直角三角形中成比例线段[下学期]

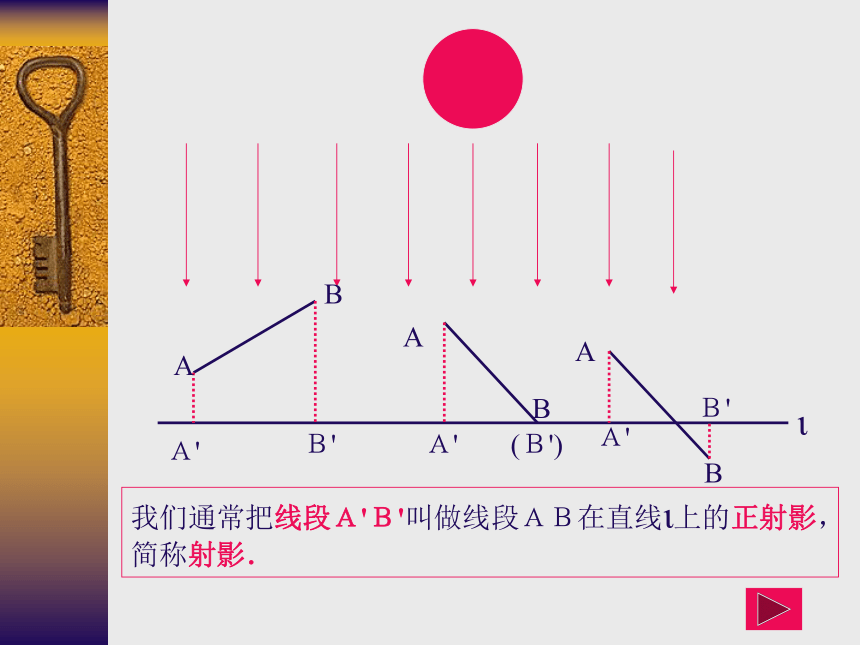
课件13张PPT。直角三角形中的成比例线段我们通常把线段Ａ'Ｂ'叫做线段ＡＢ在直线ι上的正射影，　简称射影．ABＡ'Ｂ'AA(Ｂ')Ｂ'Ａ'Ａ'BBι填空：如右图，Ｒt?ＡＢＣ中，ＣＤ是斜边上的高线。（１）直角边ＡＣ在斜边ＡＢ上的射影
　是线段　　　
（２）直角边ＢＣ在斜边AB上的射影
　是线段　　　
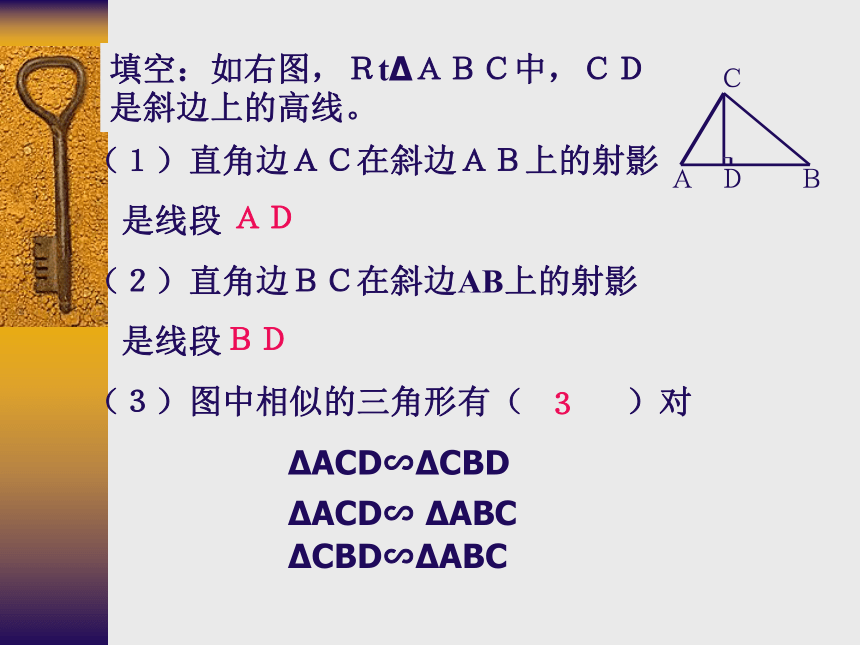
（３）图中相似的三角形有（　　　）对
ＣＤＡＢＡＤＢＤ３?ACD∽?CBD?ACD∽ ?ABC?CBD∽?ABC
?ACD∽?CBD ?ACD∽ ?ABC ?CBD∽?ABC
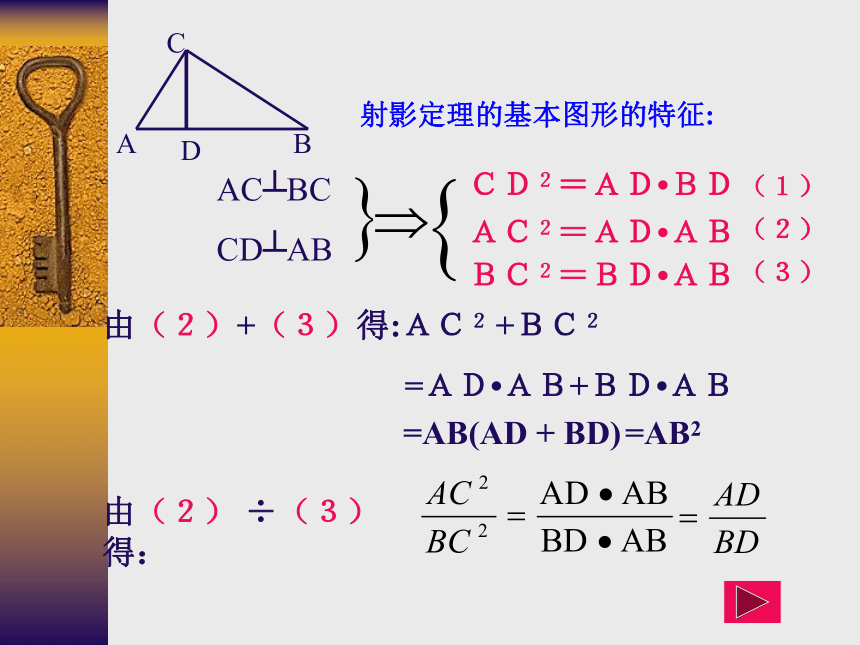
ＣＤ２＝ＡＤ?ＢＤＡＣ２＝ＡＤ?ＡＢＢＣ２＝ＢＤ?ＡＢ（１）（２）（３）直角三角形中，　　　　　　是两条直角边在斜边上的射影的比例中项；　　　　　　是这条直角边在斜边上的射影和斜边的比例中项。斜边上的高线每一条直角边射影定理：CADBB射影定理的基本图形的特征:
AC┴BC
CD┴AB
ＣＤ２＝ＡＤ?ＢＤＡＣ２＝ＡＤ?ＡＢＢＣ２＝ＢＤ?ＡＢ（１）（２）（３）由（２）+（３）得:ＡＣ２ +ＢＣ２
　　　　　　　　　=ＡＤ?ＡＢ+ＢＤ?ＡＢ=AB(AD + BD)=AB2由（２） ÷（３）得：例1　 如图，若AD=2ｃｍ，ＤＢ＝６ｃｍ，求ＣＤ，ＡＣ，ＢＣ的长。ＣＤAB解:答:ＣＤ，ＡＣ，ＢＣ的长分别为由上例可以看出：已知线段ＡＤ、ＤＢ、ＣＤ、ＡＣ、ＢＣ、ＡＢ中的两条线段的长度，就可以利用射影定理和勾股定理求出其它的四条线段的长度。填空：ＣＤ是Ｒｔ?ＡＢＣ的斜边ＡＢ上的高线，
（１）ＡＤ＝９ｃｍ，ＤＢ＝４ｃｍ，则ＣＤ＝　　ｃｍ，　　　ＡＣ＝　　ｃｍ。
（２）ＡＢ＝４ｃｍ，ＢＣ＝２ｃｍ，则ＢＤ＝　　ｃｍ，　　　
　　　ＣＤ＝　　ｃｍ。
（３）ＣＤ＝３ｃｍ，ＢＣ＝５ｃｍ，则ＡＢ＝　　ｃｍ，　　　
　　　ＡＣ＝　　ｃｍ。
（４）ＢＤ＝３ｃｍ，ＡＣ＝２ｃｍ，则ＣＤ＝　　ｃｍ，
ＢＣ＝　　ｃｍ。
（５）若ＡＣ:ＢＣ＝２ :３，则ＡＤ:ＢＤ＝　　　。
６４:９１例２　如右图，ＣＤ是Ｒｔ?ＡＢＣ的斜边上的高线，过Ｄ作ＤＥ┴ＡＣ，ＤＦ┴ＢＣ，垂足分别为Ｅ、Ｆ。求证：
（１）ＣＥ?ＣＡ＝ＣＦ?ＣＢ
ＡＢＣＤＥＦＥＡＤＣＣＤＦＢＣＥ?ＣＡ＝ＣＦ?ＣＢ证明：（２）在原图的基础上连结ＥＦ，　　　求证：?CＥＦ∽?ＣＢＡ
证明：ＣＥ?ＣＡ＝ＣＦ?ＣＢ?CＥＦ∽?ＣＢＡ问：若∠ＡＣＢ不是直角，则第（２）题的结论还成立吗？练习：已知ＣＤ是Ｒｔ?ＡＢＣ的斜边ＡＢ上的高线，求证：ＣＡ?ＣＤ ＝ＣＢ?ＡＤ。知识小结１、一个概念２、一个定理思考题（１）如右图，已知ＢＣ２＝ＢＤ?ＡＢ，能否推出ＣＤ┴ＡＢ？如果认为不能推出，那试加一个条件并推出ＣＤ┴ＡＢ。ＡＢＣＤ（２）已知ＢＣ２＝ＢＤ?ＡＢ，
ＣＤ┴ＡＢ，ＡＣ┴ＢＣ中的两个结论，能否推出第三个结论？（３）若把ＢＣ２＝ＢＤ?ＡＢ换成ＣＤ２＝ＡＤ?ＢＤ或ＡＣ２＝ＡＤ?ＡＢ呢？（４）已知ＢＣ２＝ＢＤ?ＡＢ，ＣＤ２＝ＡＤ?ＢＤ，ＡＣ２＝ＡＤ?ＡＢ，ＣＤ┴ＡＢ，ＡＣ┴ＢＣ这五个结论中的任意两个，能否推出另外三个结论？作业1、温习课本
2、数学作业本