4.1比例线段(3)[上学期]
图片预览







文档简介
课件22张PPT。§4.1 比例线段(3)第四章 相似三角形浙教版九年级《数学》上册九年级数学备课组
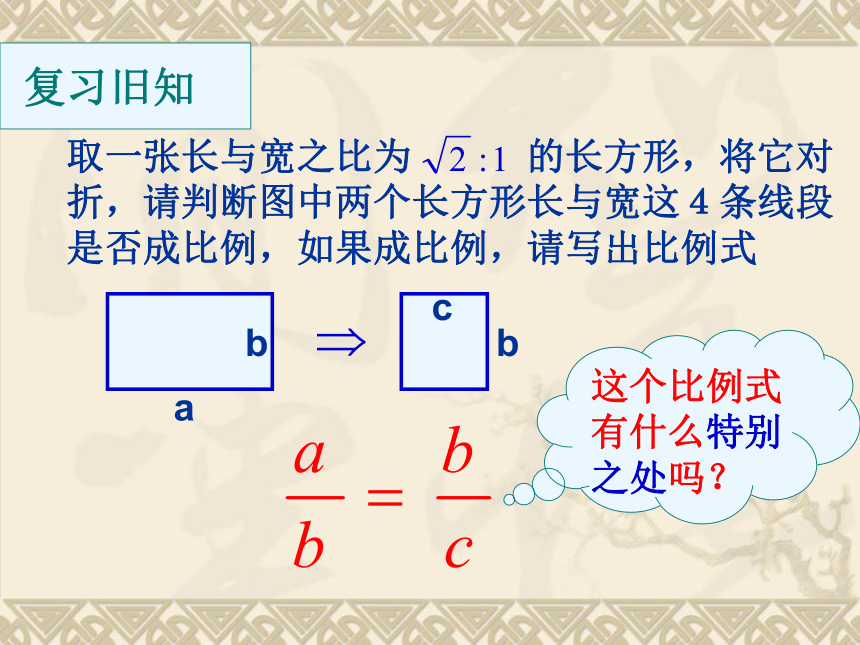
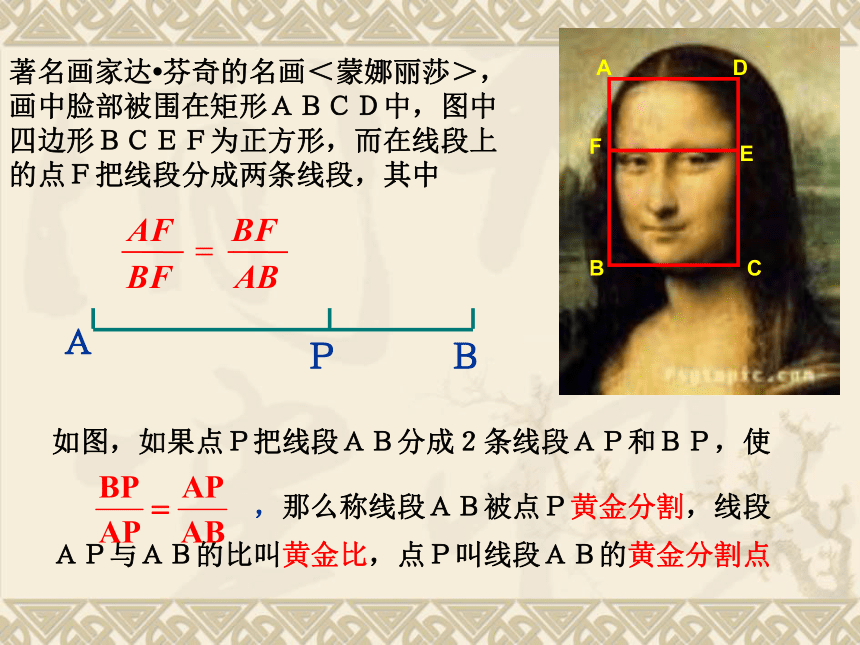
2006.10.取一张长与宽之比为 的长方形,将它对折,请判断图中两个长方形长与宽这4条线段是否成比例,如果成比例,请写出比例式这个比例式有什么特别之处吗?一般地,如果三个数a,b,c满足比例式 ,则b就叫a,c的比例中项著名画家达?芬奇的名画<蒙娜丽莎>,画中脸部被围在矩形ABCD中,图中四边形BCEF为正方形,而在线段上的点F把线段分成两条线段,其中DCE如图,如果点P把线段AB分成2条线段AP和BP,使
,那么称线段AB被点P黄金分割,线段AP与AB的比叫黄金比,点P叫线段AB的黄金分割点EF利用一元二次方程的知识,可以求出黄金比的数值几,即 的值设AB=a, AP=x 著名画家达·芬奇的蒙娜丽莎,拉斐尔笔下温和、俊秀的圣母像,也利用这一黄金分割的比例,。1483年左右,达·芬奇画的一幅未完成的油画,包围着圣杰罗姆躯体的黑线,就是一个黄金分割的矩形,当时达·芬奇似乎有意利用这一黄金分割的比值。“检阅”是法国印象派画家舍勒特的一幅油画,它的画杠结构比例也正是0.618的比值.英国在画家斐拉克曼的名著《希腊的神话和传说》一书中,共绘有96幅美人图。每一幅画上的美人都妩媚无比婀娜多姿。如果仔细量一下她们身体的比例也都与雅典娜相似。
FE追溯黄金分割的历史文化 早在古希腊,数学家、天文学家欧多克索斯(Eudoxus,约前400——前347)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题.
而发现黄金分割的是古希腊哲学家毕达哥拉斯。一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定0.618 :1的比例截断最优美。后来,意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。 天文学家开普勒(Johannes Kepler,1571——1630)把这种分割线段的方法称为神圣分割,并指出,毕达哥拉斯定理(勾股定理)和黄金分割“是几何中的双宝,前者好比黄金,后者堪称珠玉”。 而历史上最早正式在书中使用“黄金分割”这个名称的是欧姆(Martin Ohm,1792——1872)。19世纪以后,“黄金分割”的说法逐渐流行起来…。 她的上半
身和下半身的比值接近
0.618. 世界艺术珍品——维纳斯女神 ,她是西元前一
百多年希腊雕塑鼎盛时
期的代表作,黄金分割原理最初运用于雕塑和建筑数学美的魅力 1古埃及胡夫金字塔古希腊巴特农神庙文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高这比都接近于0.618.古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.你知道芭蕾舞演员跳舞时为什么要掂起脚尖吗?芭蕾舞演员的身段是苗条的,但下半身与身高的比值也只有0.58左右,演员在表演时掂起脚尖,身高就可以增加6-8cm.这时比值就接近0.618了,给人以更为优美的艺术形象.芭蕾舞黄金分割 与生活由黄金分割画出的正五角星形,有庄严雄健之美.耐人寻味的0.618打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618; 节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置; 生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?468m?468×0.618≈289.2m有些植物茎上,相邻两张叶子成137°28′的角,这种角度
使植物通风和采光的效果最佳,这一度数与怎样的角的度数成黄金比?AB你们知道如何确定线段AB的黄金分割点所在的位置吗?例5:
已知线段AB=a,用直尺和圆规作出它的黄金分割点悟出一个新自己什么是黄金分割.
如何去确定黄金分割点或黄金比.
将所学知识网络化.
要用数学美去装点和美化生活.
与同伴谈谈你对黄金分割的收获与体会.
试试看!1.作顶角为36°的等腰△ABC;量出
底BC与腰AB的长度,计算: ;
2.作∠B的平分线,交AC于点D,量出CD的长度,
再计算: . (精确到0.001)0.6180.618☆再作∠C的平分线,交BD于E,
△CDE也是黄金三角形……☆顶角为36°的等腰三角形称为 黄金三角形 ☆点D是线段AC的黄金分割点.
2006.10.取一张长与宽之比为 的长方形,将它对折,请判断图中两个长方形长与宽这4条线段是否成比例,如果成比例,请写出比例式这个比例式有什么特别之处吗?一般地,如果三个数a,b,c满足比例式 ,则b就叫a,c的比例中项著名画家达?芬奇的名画<蒙娜丽莎>,画中脸部被围在矩形ABCD中,图中四边形BCEF为正方形,而在线段上的点F把线段分成两条线段,其中DCE如图,如果点P把线段AB分成2条线段AP和BP,使
,那么称线段AB被点P黄金分割,线段AP与AB的比叫黄金比,点P叫线段AB的黄金分割点EF利用一元二次方程的知识,可以求出黄金比的数值几,即 的值设AB=a, AP=x 著名画家达·芬奇的蒙娜丽莎,拉斐尔笔下温和、俊秀的圣母像,也利用这一黄金分割的比例,。1483年左右,达·芬奇画的一幅未完成的油画,包围着圣杰罗姆躯体的黑线,就是一个黄金分割的矩形,当时达·芬奇似乎有意利用这一黄金分割的比值。“检阅”是法国印象派画家舍勒特的一幅油画,它的画杠结构比例也正是0.618的比值.英国在画家斐拉克曼的名著《希腊的神话和传说》一书中,共绘有96幅美人图。每一幅画上的美人都妩媚无比婀娜多姿。如果仔细量一下她们身体的比例也都与雅典娜相似。
FE追溯黄金分割的历史文化 早在古希腊,数学家、天文学家欧多克索斯(Eudoxus,约前400——前347)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题.
而发现黄金分割的是古希腊哲学家毕达哥拉斯。一天,毕达哥拉斯从一家铁匠铺路过,被铺子中那有节奏的叮叮当当的打铁声所吸引,便站在那里仔细聆听,似乎这声音中隐匿着什么秘密。他走进作坊,拿出一把尺量了一下铁锤和铁砧的尺寸,发现它们之间存在着一种十分和谐的关系。回到家里,毕达哥拉斯拿出一根线,想将它分为两段。怎样分才最好呢?经过反复比较,他最后确定0.618 :1的比例截断最优美。后来,意大利著名科学家、艺术家达·芬奇给这个比例冠以“黄金”二字的美名。 天文学家开普勒(Johannes Kepler,1571——1630)把这种分割线段的方法称为神圣分割,并指出,毕达哥拉斯定理(勾股定理)和黄金分割“是几何中的双宝,前者好比黄金,后者堪称珠玉”。 而历史上最早正式在书中使用“黄金分割”这个名称的是欧姆(Martin Ohm,1792——1872)。19世纪以后,“黄金分割”的说法逐渐流行起来…。 她的上半
身和下半身的比值接近
0.618. 世界艺术珍品——维纳斯女神 ,她是西元前一
百多年希腊雕塑鼎盛时
期的代表作,黄金分割原理最初运用于雕塑和建筑数学美的魅力 1古埃及胡夫金字塔古希腊巴特农神庙文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高这比都接近于0.618.古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.你知道芭蕾舞演员跳舞时为什么要掂起脚尖吗?芭蕾舞演员的身段是苗条的,但下半身与身高的比值也只有0.58左右,演员在表演时掂起脚尖,身高就可以增加6-8cm.这时比值就接近0.618了,给人以更为优美的艺术形象.芭蕾舞黄金分割 与生活由黄金分割画出的正五角星形,有庄严雄健之美.耐人寻味的0.618打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618; 节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置; 生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于8开、16开、32开等,都仍然是近似的黄金矩形。上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?468m?468×0.618≈289.2m有些植物茎上,相邻两张叶子成137°28′的角,这种角度
使植物通风和采光的效果最佳,这一度数与怎样的角的度数成黄金比?AB你们知道如何确定线段AB的黄金分割点所在的位置吗?例5:
已知线段AB=a,用直尺和圆规作出它的黄金分割点悟出一个新自己什么是黄金分割.
如何去确定黄金分割点或黄金比.
将所学知识网络化.
要用数学美去装点和美化生活.
与同伴谈谈你对黄金分割的收获与体会.
试试看!1.作顶角为36°的等腰△ABC;量出
底BC与腰AB的长度,计算: ;
2.作∠B的平分线,交AC于点D,量出CD的长度,
再计算: . (精确到0.001)0.6180.618☆再作∠C的平分线,交BD于E,
△CDE也是黄金三角形……☆顶角为36°的等腰三角形称为 黄金三角形 ☆点D是线段AC的黄金分割点.
同课章节目录
