4.2 相似三角形[上学期]

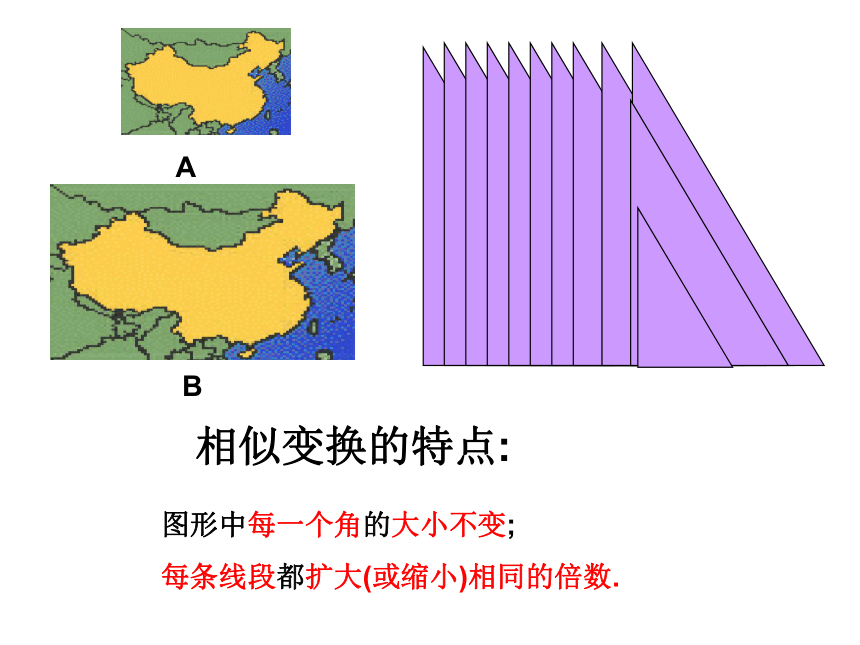
课件15张PPT。相似变换的特点:图形中每一个角的大小不变;
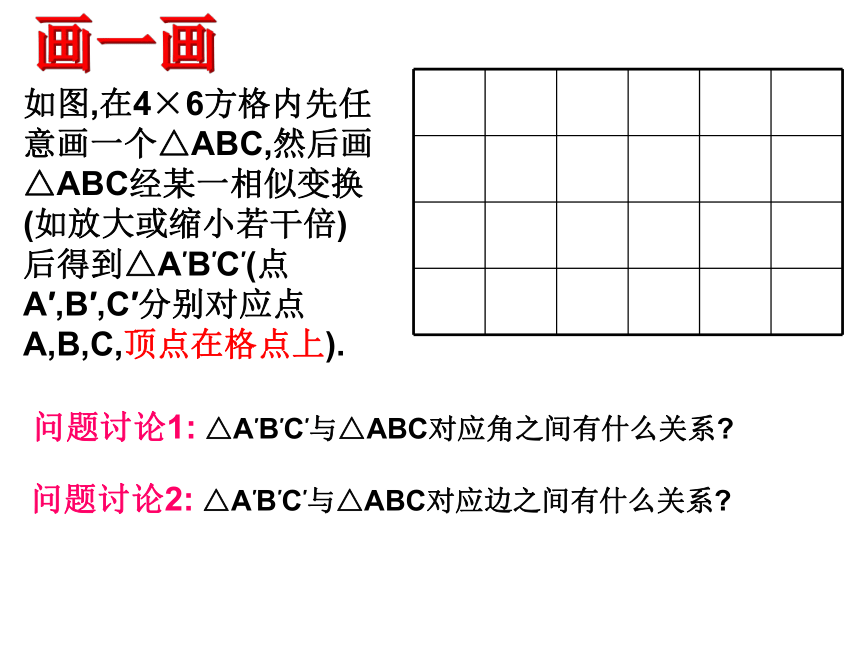
每条线段都扩大(或缩小)相同的倍数.如图,在4×6方格内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?画一画表示为：
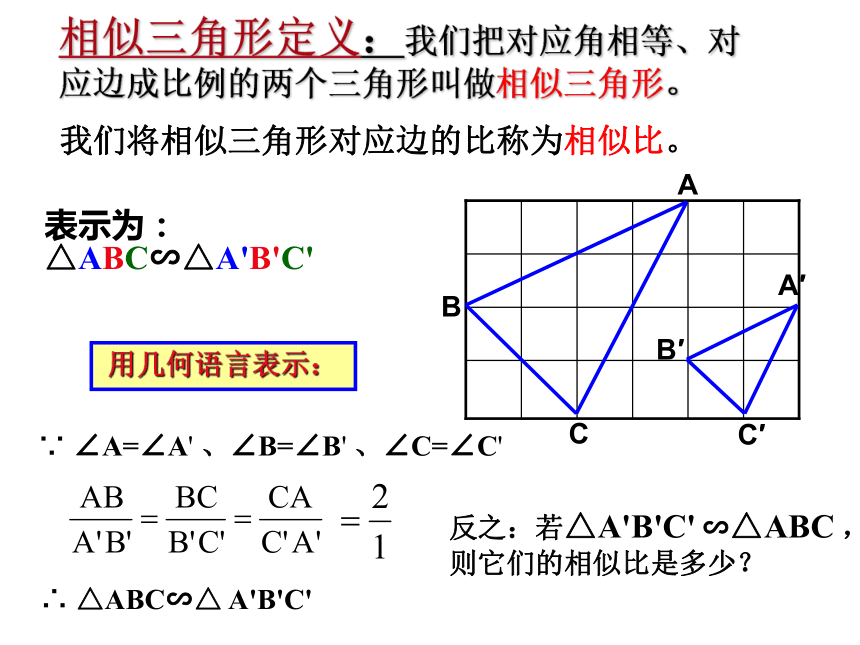
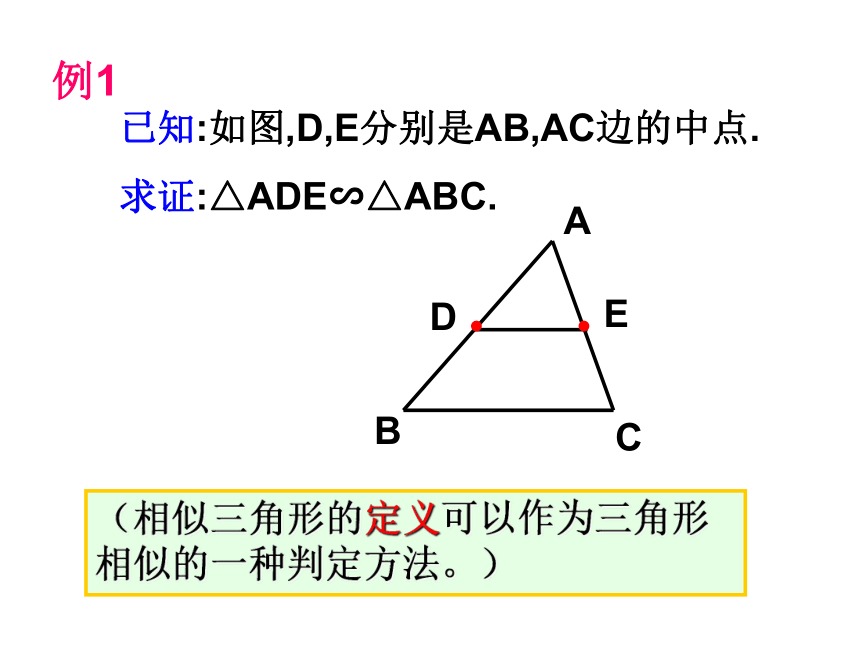
△ABC∽△A'B'C' CABB′A′C′相似三角形定义：我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。用几何语言表示：∵ ∠A=∠A' 、∠B=∠B' 、∠C=∠C'∴ △ABC∽△ A'B'C' 我们将相似三角形对应边的比称为相似比。 反之：若△A'B'C' ∽△ABC ，则它们的相似比是多少？ 已知:如图,D,E分别是AB,AC边的中点.
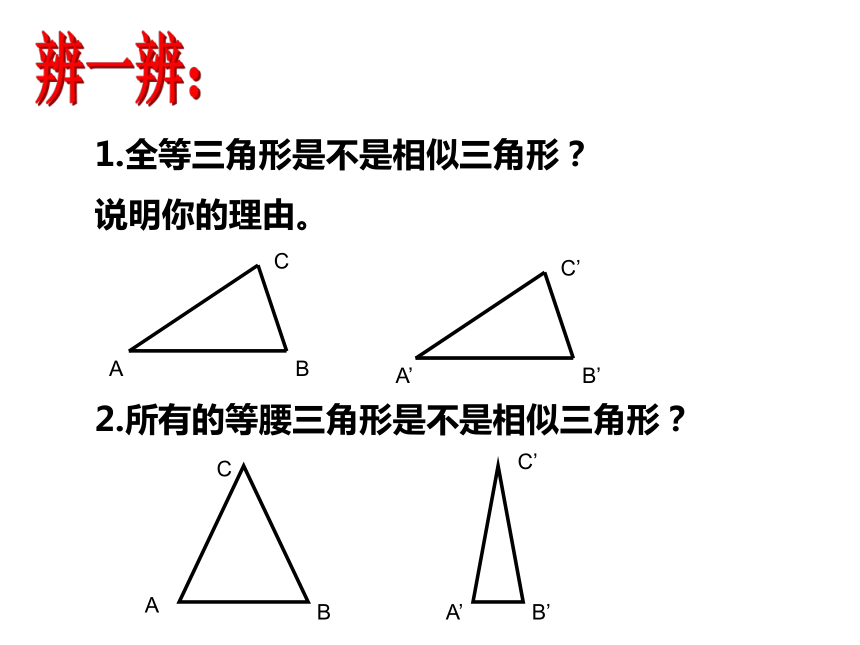
求证:△ADE∽△ABC.EDCBA例1（相似三角形的定义可以作为三角形相似的一种判定方法。）1.全等三角形是不是相似三角形？
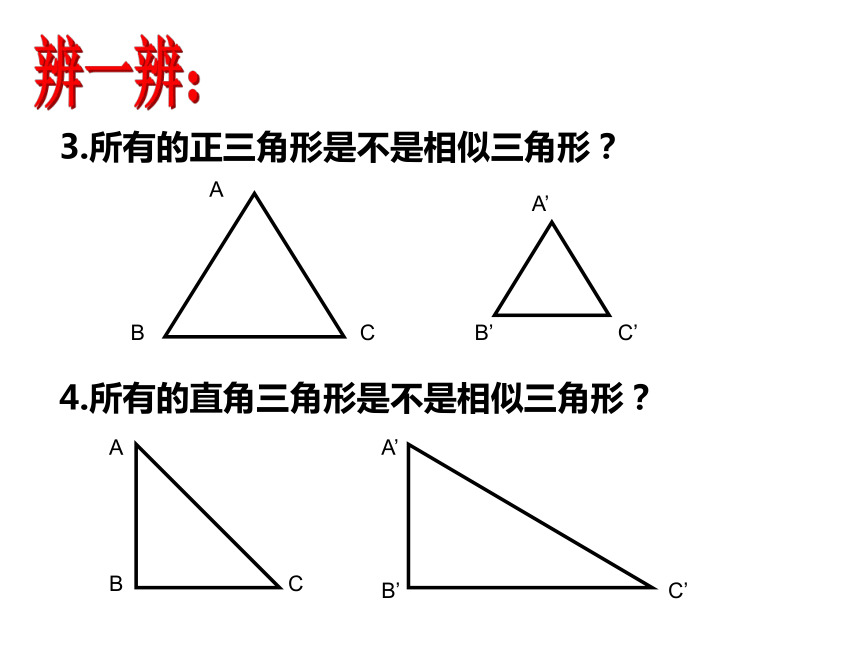
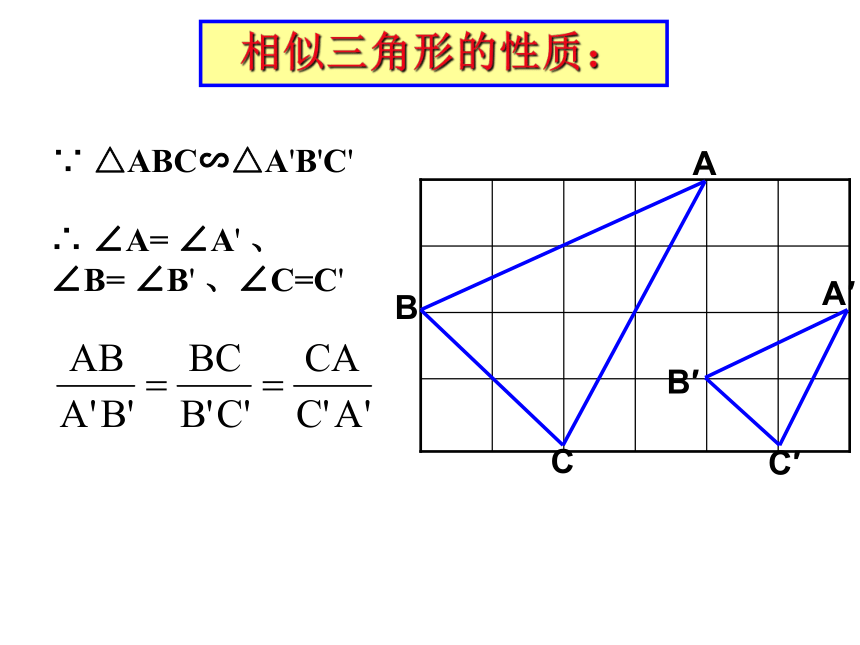
说明你的理由。2.所有的等腰三角形是不是相似三角形？辨一辨：4.所有的直角三角形是不是相似三角形？3.所有的正三角形是不是相似三角形？辨一辨：相似三角形的性质：∴ ∠A= ∠A' 、
∠B= ∠B' 、∠C=C'∵ △ABC∽△A'B'C'如图，△ADE∽ △ABC，且点D与点B对应，根据图形分别说出两个三角形的对应边和对应角？说一说例2：如图，D、E分别是△ABC的AB，AC边上的点，△ABC∽ △ADE，且点D与点B对应 。（1）若∠B=30°， ∠1=80 °，
则∠2 =_______∠C =_______例2：如图，D、E分别是△ABC的AB，AC边上的点，△ABC∽ △ADE，且点D与点B对应 。（2）若 AD:AB=1:3 ，BC=9cm，
求DE的长。AD:DB=1:2ABCDE9AD:DB=2:3 在下面的两组图形中，各有两个相似三角形，
试确定x ,y ,m ,n 的值. 练习：已知△ABC∽ △DEF，（1）若△ABC的三边为2,3,4, △DEF的最大边为8,
求其余两边.（2）若△ABC的三边为2,3,4, △ABC的一边为8,
求其余两边.想一想：对应角相等， 对应边成比例的两个三角形, 叫做相似三角形。如果△ ABC∽ △DEF,相似三角形的对应角相等, 对应边对应成比例.△ABC与△DEF相似，就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上！那么∠A =∠D,∠B =∠E,∠C =∠F.1. 定义2. 性质1.如图，D是AB上的一点。 △ABC∽ △ACD ，D与C对应，且∠1= 65°，AD：AC＝2：3,
（1）求∠ACB的度数；随堂练习（2） AB：AC的值2、如图，AB，CD相交于点0, △AOC∽ △BOD 。
（1）如果OC：OD＝1：2,AC＝5,求BD的长；
（2）如果∠A＝35°, ∠AOC＝100°,求∠D的度数。