相似三角形复习[上学期]

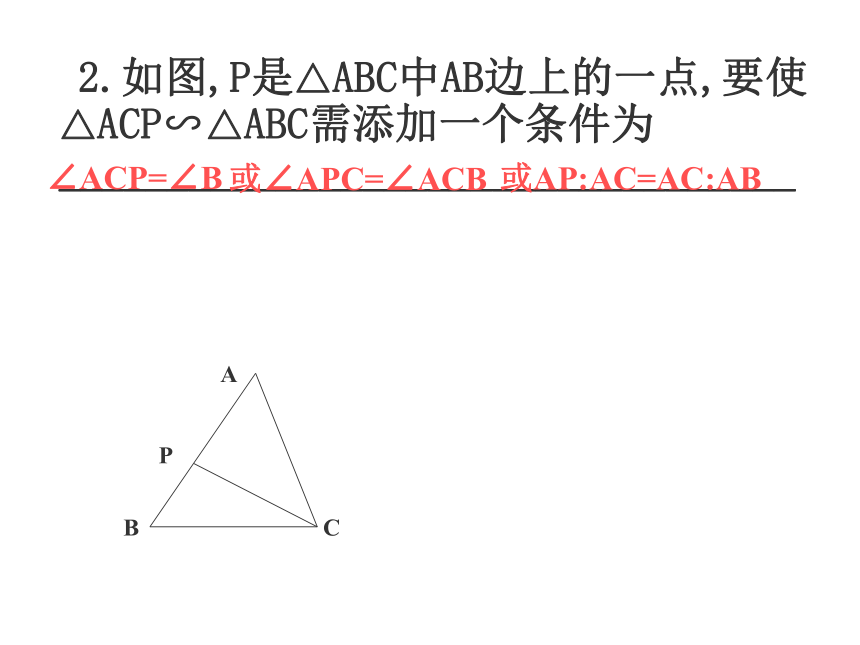
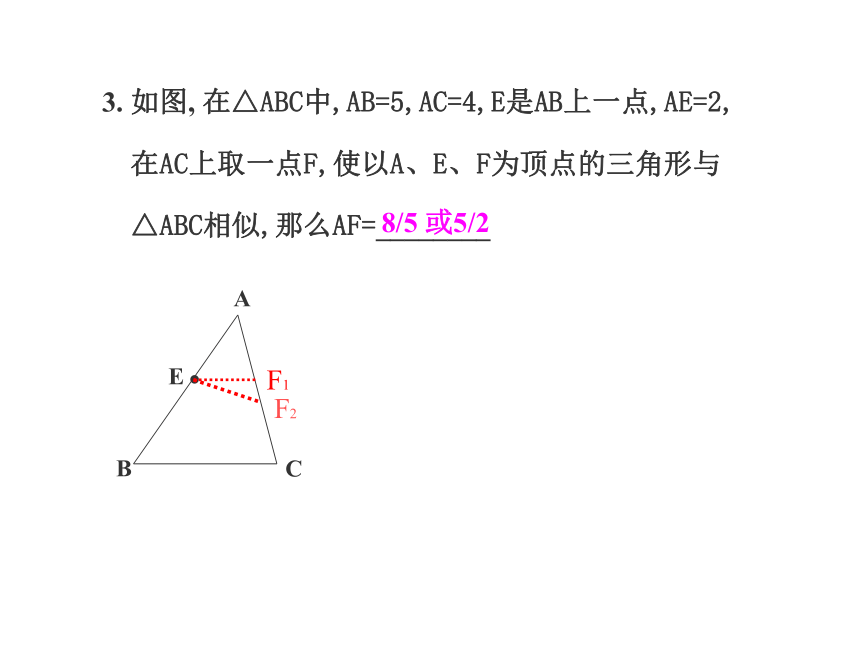
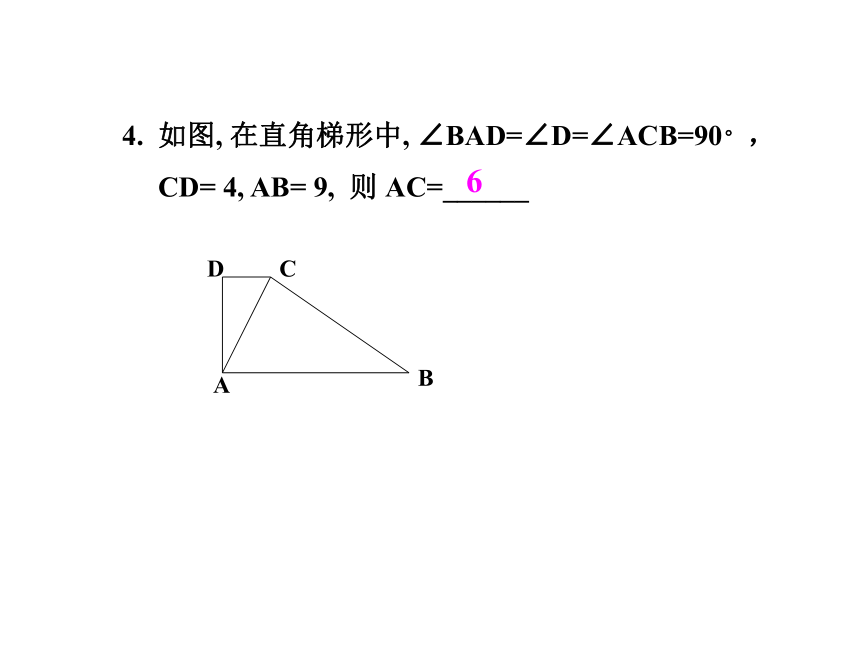
课件20张PPT。相似三角形复习课一.比例线段知识要点比例中项：练习：一.比例线段知识要点3.黄金分割：练习：4一.比例线段知识要点练习：1.相似三角形的定义：对应角相等、对应边成比例的三角形叫做相似三角形。2.相似比：相似三角形的对应边的比，叫做相似三角形的相似比。练习：二.相似三角形知识要点3.相似三角形的判定：（1）平行于三角形一边的直线截其它两边(或两边的延长线)相交；（2）两角对应相等；（3）两边对应成比例且夹角相等；（4）三边对应成比例；（5）Rt 中被斜边上的高分成的两个三角形相似。练习：4知识要点二.相似三角形 2.如图,P是△ABC中AB边上的一点,要使△ACP∽△ABC需添加一个条件为__________________________________ ∠ACP=∠B或∠APC=∠ACB或AP:AC=AC:AB8/5或5/26练习：(2)以正方形的边长等量过渡.（3）请找出图中的相似三角形1.如图, 在△ABC中,∠ACB= 90。，四边形BEDC为正方
形, AE交BC于F, FG∥AC交AB于G. 求证: FC=FG. 证明: ∵四边形BEDC为正方形∴CF∥DE DE=BE ∴△ACF∽△ADE∴ ①又∵FG ∥AC∥BE∴△AGF∽△ABE∴ ②由①②可得：又∵ DE=BE∴FC=FG范例例2 如图，已知：DE ∥BC，DC和BE相交于P点，连结AP交DE于M，延长AP交BC于N点，求证：DM=ME，BN=NC。分析：∽同理可证：BN=NC(1) ∵ 得
∴ΔABC∽ΔADE ∴ ∠BAC=∠DAE∴ ∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE(2) 由∴∵∠BAD=∠CAE ∴ΔABD∽ΔACE∴∴ 证明：例3 如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足怎样关系时, △PCA∽ △BDP.
(2)当△PCA∽ △BDP时,求∠APB的度数.练习：1.如图，点E是边长为1的正方形ABCD的边AB上的点,且AE:AB=1:4,F是边AD上的点,问当F在什么位置时, △AEF和△CDF相似..2.如图,已知△ABC中,BC=8cm,AB=AC=5cm,一动点P在底边上从B点向C点以0.25cm/s的速度移动,当点P运动到和腰垂直的位置时,求P点的运动时间t.DD4.相似三角形的性质：对应角相等，对应边成比例，对应高、对应中线、对应角平分线的比都等于相似比，周长比等于相似比，面积比等于相似比的平方。练习：1.地图上的1cm2面积表示实际100m2的面积，则该地图的比例尺是__________.2.两个相似三角形的面积比为m,周长比为2,则m2=________.163.边长为2的正三角形被平行一边的直线分成等积的两部分,
其中一部分是梯形,则这个梯形的中位线长为_______.二.相似三角形知识要点1︰1000三.相似三角形性质的应用:范例2. 如图, AD⊥BC, D为垂足, AD=8, BC=10, EFGH是△ABC内
接矩形,(H、G是BC上的两个动点,但H不到达点B, G不到达
点C) 设 EH=x,EF=y
(1)求y与x之间的函数关系式,并求自变量x的取值范围;
(2)当EF+EH=9时,求矩形EFGH的周长和面积.练习：