4.4相似三角形的性质[下学期]

课件17张PPT。课前音乐欣赏 轻松走进数学课堂相似三角形的性质主讲: 陈海飞1.回忆全等三角形的性质:
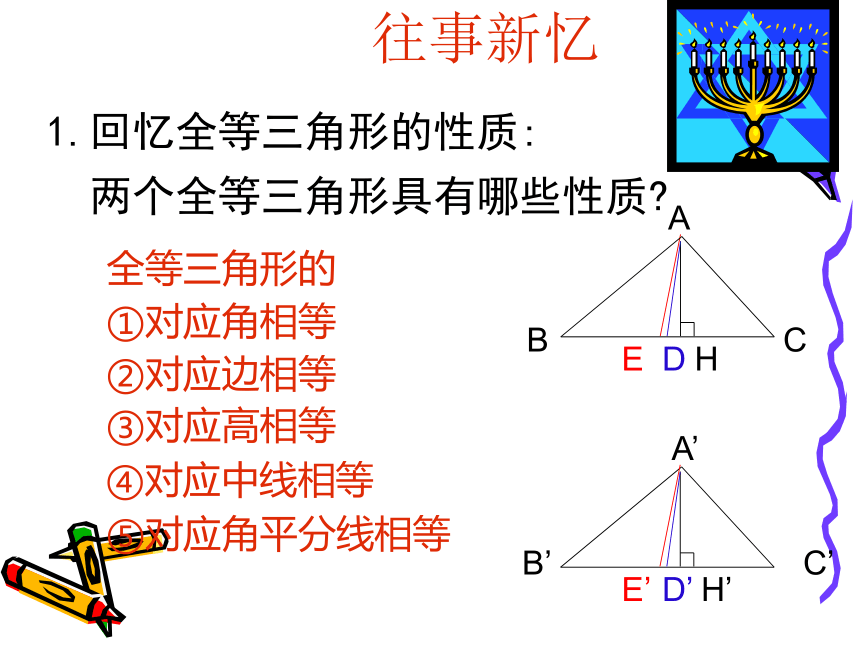
两个全等三角形具有哪些性质?往事新忆⑤对应角平分线相等HDE全等三角形的
①对应角相等
②对应边相等③对应高相等④对应中线相等H’D’E’新知猜想展开想象的翅膀:
相似三角形的对应角、对应边、
对应高、对应中线及对应角平分线
有何关系？相似三角形的性质根据相似三角形的定义我们可以知道哪些性质？对应角相等，对应边成比例。
我们来研究其它性质J我们把对应边的比值称为相似比
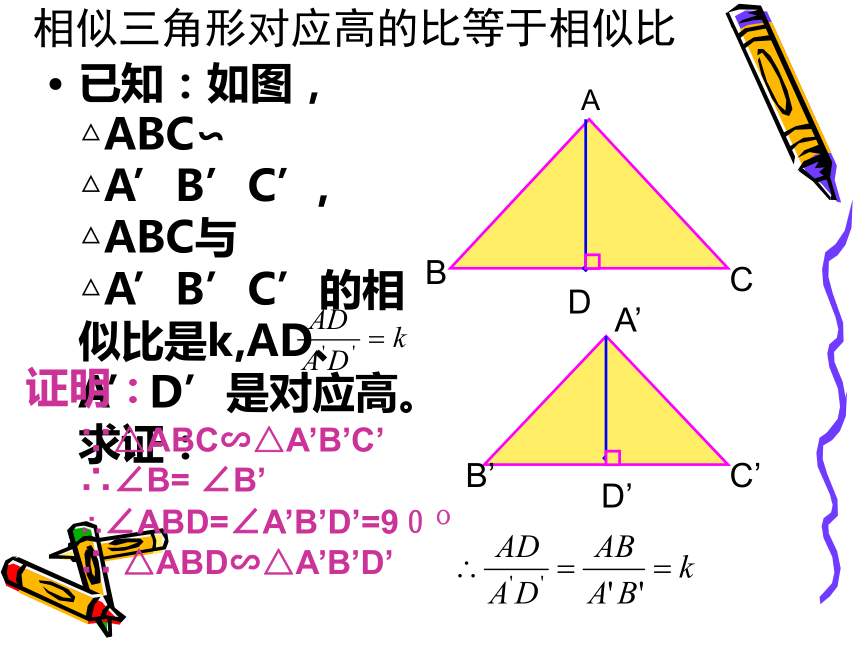
猜想EQ相似三角形对应高的比是否等于相似比已知：如图，△ABC∽ △A’B’C’, △ABC与 △A’B’C’的相似比是k,AD、A’D’是对应高。求证：
ABCB’A’C’DD’证明：∵△ABC∽△A’B’C’
∴∠B= ∠B’∴∠ABD=∠A’B’D’=9０Ｏ
∴ △ABD∽△A’B’D’相似三角形对应高的比等于相似比由例题我们可以得到什么样的结论？定理：相似三角形的对应高的比，
等于相似比。
我也做一做：相信自己，走向成功A组，求证：相似三角形对应中线的比等于相似比。B组，求证：相似三角形对应角平分线的比等于相似比。C组，求证：相似三角形的周长等于相似比。由以上得到什么样的结论？定理：相似三角形的对应高的比，对应中线
的比与对应角平分线的比等于相似比。
相似三角形的周长的比等于相似比。填空题1、如图，AD＝3，BD＝1，DE∥BC，
DF∥AC，EG∥AB。（1）△ADE和△EGC的相似比是 ，对应高的比是 。（2） △ABC和△DBF的相似比 ，对应角平分线的比 ，对应中线的比是 。3∶ 14 ∶14 ∶14 ∶13 ∶12、两个相似三角形的相似比为1 ∶3，它们的对应高的比是 。
3、两个相似三角形的相似比为2∶3，它们的对应中线的比是 。
4、两个相似三角形的对应高的比为3∶5，它们的对角平分线的比是 。
5、两个相似三角形的对应中线的比为9∶16，它们的相似比是 。
6、两个相似三角形的对应角平分线的比为4∶9，它们的对应高的比是 。
7、两个相似三角形各自的最长边分别是7cm、5cm，它们的对应高的比是 。1∶32∶33∶59∶164∶97∶5实战演习已知：如图，△ABC∽ △A’B’C’, △ABC与 △A’B’C’的相似比是k,AD、A’D’是对应高。求ABCB’A’C’DD’S△ABC
————
S△A’B’C’=?S△ABC
————
S△A’B’C’解：k2定理：相似三角形的面积的比等于相似比的平方。1、如果把一个三角形按照下面的条件改成和它相似的三角形：
（1）把边长扩大为原来的100倍，那么面积扩大为原来的多少倍？
（2）把面积扩大为原来的100倍，那么边长扩大为原来的多少倍？
2、两个相似三角形周长比是1：3，它们的面积比是多少？
3、两个相似三角形面积的比是4：25，边长的比是多少？
4、两个三角形周长比是2/3，它们的面积之比是否　 是4/9。练习例2.已知:?ABC中，点D，E，F，分别在边AB，AC，BC上，DE??BC，EF??AB， ，S?ABC=S。求S BFED

ABCDEF3、ΔABC中，AE是角平分线，D是AB上的一点，CD交AE于G，∠ACD=∠B，且AC=2AD.则ΔACD∽ Δ______.它们的相似比K =_______,ABCED总结： 通过今天的学习你有何收获？从你身边同学的身上你学到了什么？