相似三角形的应用复习[下学期]

(共23张PPT)
相似三角形的
实际应用
大溪二中 张菊平
MH BH
5 15
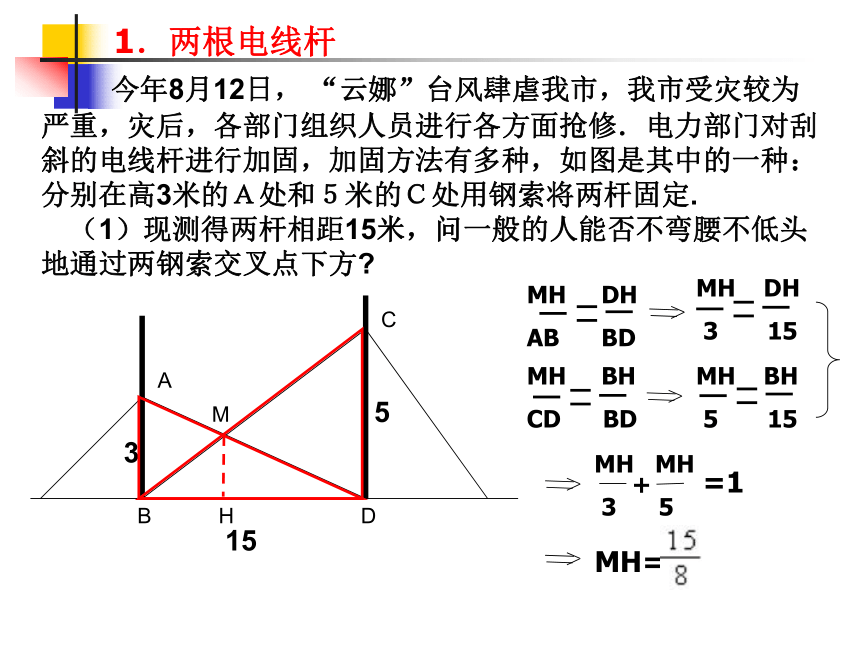
1．两根电线杆
　 今年8月12日， “云娜”台风肆虐我市，我市受灾较为严重，灾后，各部门组织人员进行各方面抢修．电力部门对刮斜的电线杆进行加固，加固方法有多种，如图是其中的一种：分别在高3米的Ａ处和５米的Ｃ处用钢索将两杆固定. 　（1）现测得两杆相距15米，问一般的人能否不弯腰不低头地通过两钢索交叉点下方 　　　　
A
B
C
D
M
H
3
5
15
MH DH
AB BD
MH BH
CD BD
MH DH
3 15
MH MH
3 5
+
=1
MH=
MH BH
5
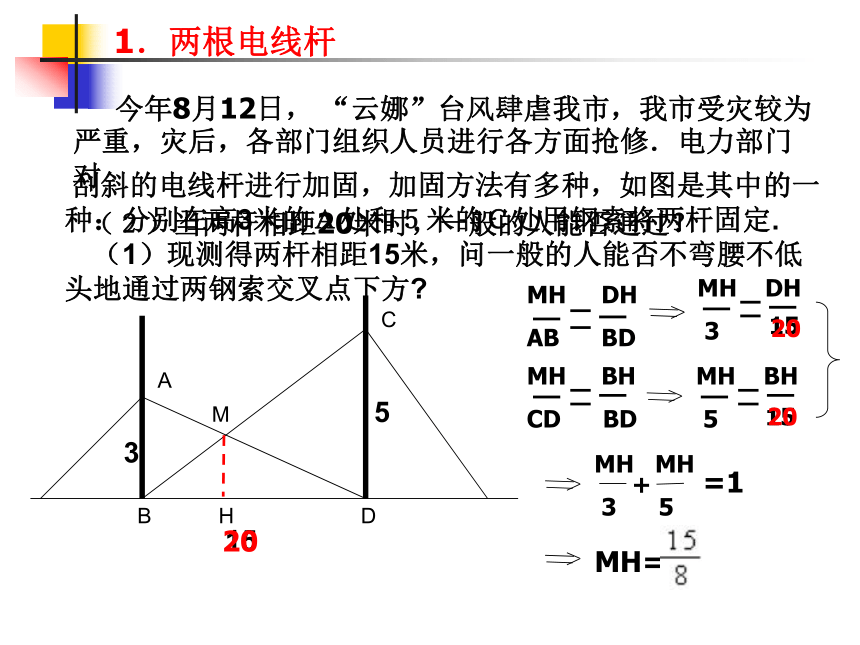
1．两根电线杆
　　
刮斜的电线杆进行加固，加固方法有多种，如图是其中的一种：分别在高3米的Ａ处和５米的Ｃ处用钢索将两杆固定. 　（1）现测得两杆相距15米，问一般的人能否不弯腰不低头地通过两钢索交叉点下方
A
B
C
D
M
H
3
5
15
MH DH
AB BD
MH BH
CD BD
MH DH
3
MH MH
3 5
+
=1
MH=
（２）当两杆相距20米时，一般的人能否通过？
今年8月12日， “云娜”台风肆虐我市，我市受灾较为严重，灾后，各部门组织人员进行各方面抢修．电力部门对
20
15
15
20
20
c BH
b BD
c DH
a BD
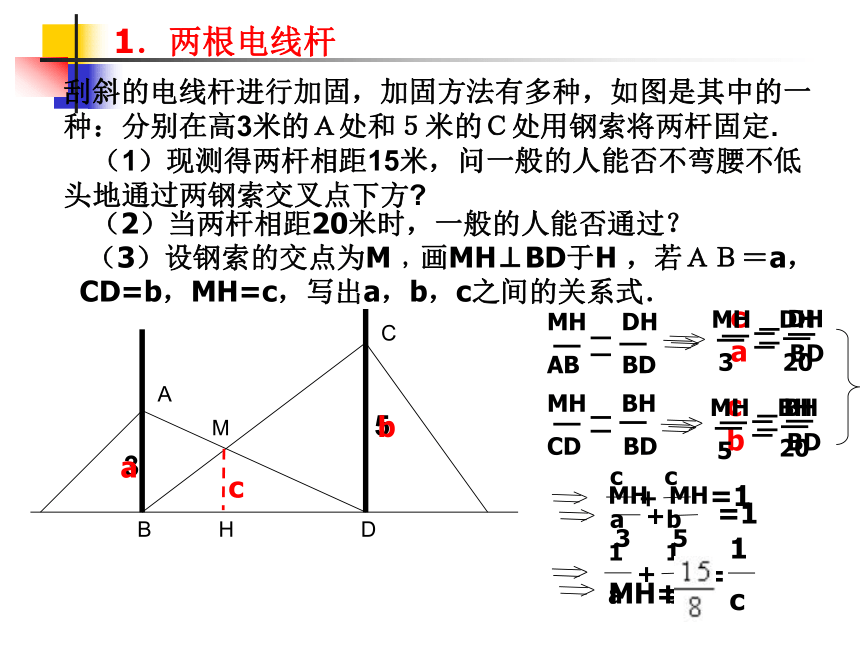
1．两根电线杆
刮斜的电线杆进行加固，加固方法有多种，如图是其中的一种：分别在高3米的Ａ处和５米的Ｃ处用钢索将两杆固定. 　（1）现测得两杆相距15米，问一般的人能否不弯腰不低头地通过两钢索交叉点下方
A
B
C
D
M
H
3
5
MH DH
AB BD
MH BH
CD BD
c c
a b
+
=1
（2）当两杆相距20米时，一般的人能否通过？
（3）设钢索的交点为M﹐画MH⊥BD于H ，若ＡＢ＝a，CD=b，MH=c，写出a，b，c之间的关系式．
a
b
c
1 1
a b
+
=
1
c
MH BH
5
MH DH
3 20
MH MH
3 5
+
=1
MH=
20
1．两根电线杆
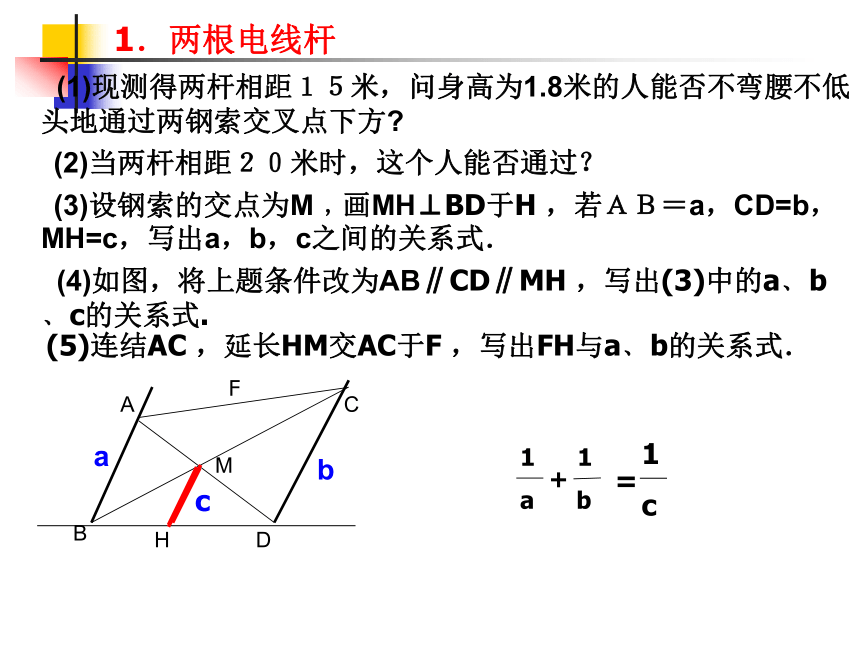
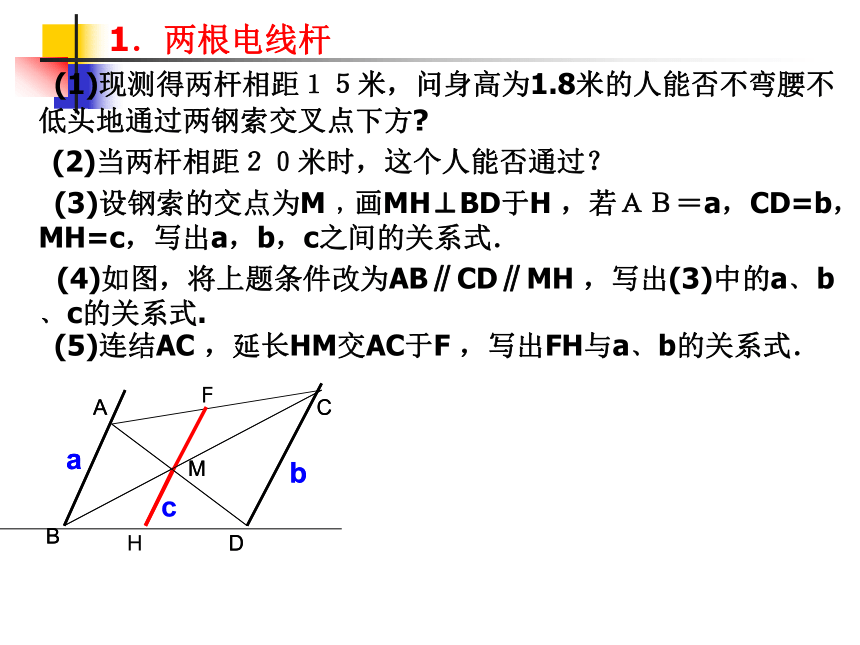
(1)现测得两杆相距１５米，问身高为1.8米的人能否不弯腰不低头地通过两钢索交叉点下方
　 (2)当两杆相距２０米时，这个人能否通过？
　 (3)设钢索的交点为M﹐画MH⊥BD于H ，若ＡＢ＝a，CD=b，MH=c，写出a，b，c之间的关系式．
(4)如图，将上题条件改为AB∥CD∥MH ，写出(3)中的a﹑b﹑c的关系式.
A
B
C
D
M
H
a
b
c
1 1
a b
+
=
1
c
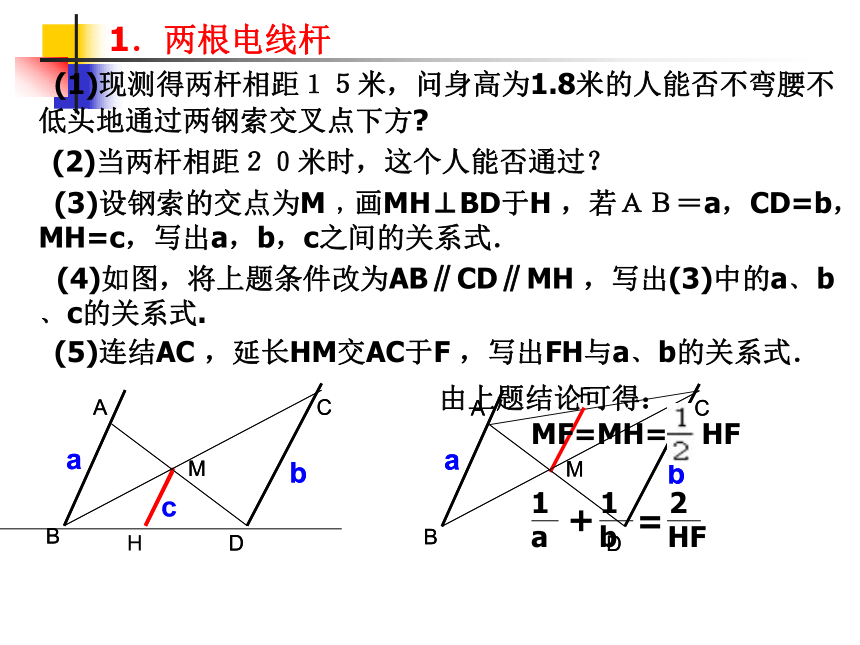
(5)连结AC ，延长HM交AC于F ，写出FH与a﹑b的关系式．
F
1．两根电线杆
A
B
C
D
M
H
a
b
c
F
A
B
C
D
M
a
b
(1)现测得两杆相距１５米，问身高为1.8米的人能否不弯腰不低头地通过两钢索交叉点下方
　 (2)当两杆相距２０米时，这个人能否通过？
　 (3)设钢索的交点为M﹐画MH⊥BD于H ，若ＡＢ＝a，CD=b，MH=c，写出a，b，c之间的关系式．
(4)如图，将上题条件改为AB∥CD∥MH ，写出(3)中的a﹑b﹑c的关系式.
(5)连结AC ，延长HM交AC于F ，写出FH与a﹑b的关系式．
1．两根电线杆
A
B
C
D
M
H
a
b
c
A
B
C
D
M
a
b
(1)现测得两杆相距１５米，问身高为1.8米的人能否不弯腰不低头地通过两钢索交叉点下方
　 (2)当两杆相距２０米时，这个人能否通过？
　 (3)设钢索的交点为M﹐画MH⊥BD于H ，若ＡＢ＝a，CD=b，MH=c，写出a，b，c之间的关系式．
(4)如图，将上题条件改为AB∥CD∥MH ，写出(3)中的a﹑b﹑c的关系式.
(5)连结AC ，延长HM交AC于F ，写出FH与a﹑b的关系式．
A
B
C
D
M
a
b
F
A
B
C
D
M
a
b
由上题结论可得：
MF=MH= HF
1 1 2
a b HF
+
=
2.测量树高
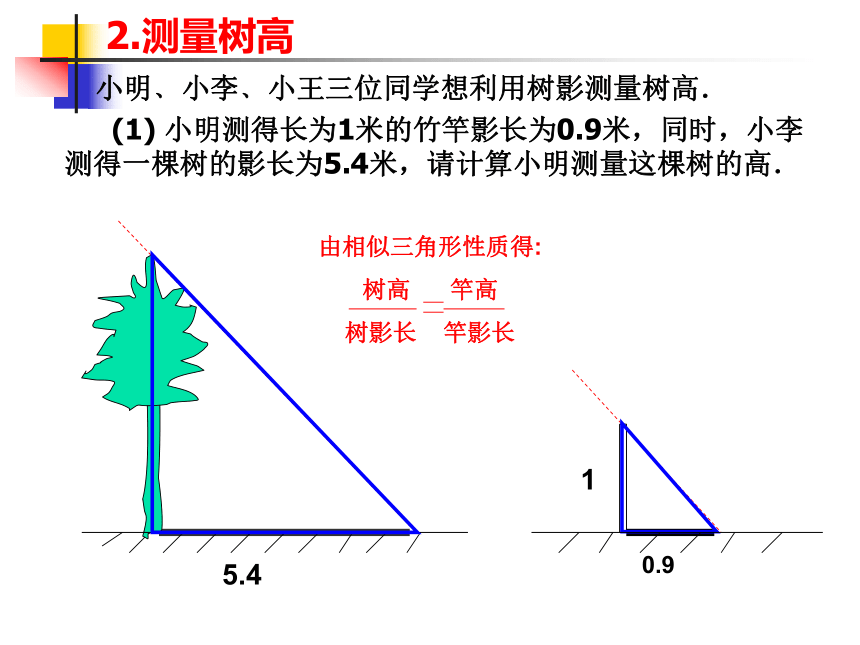
小明﹑小李﹑小王三位同学想利用树影测量树高．
　 (1) 小明测得长为1米的竹竿影长为0.9米，同时，小李测得一棵树的影长为5.4米，请计算小明测量这棵树的高．
由相似三角形性质得:
树高 竿高
树影长 竿影长
5.4
0.9
1
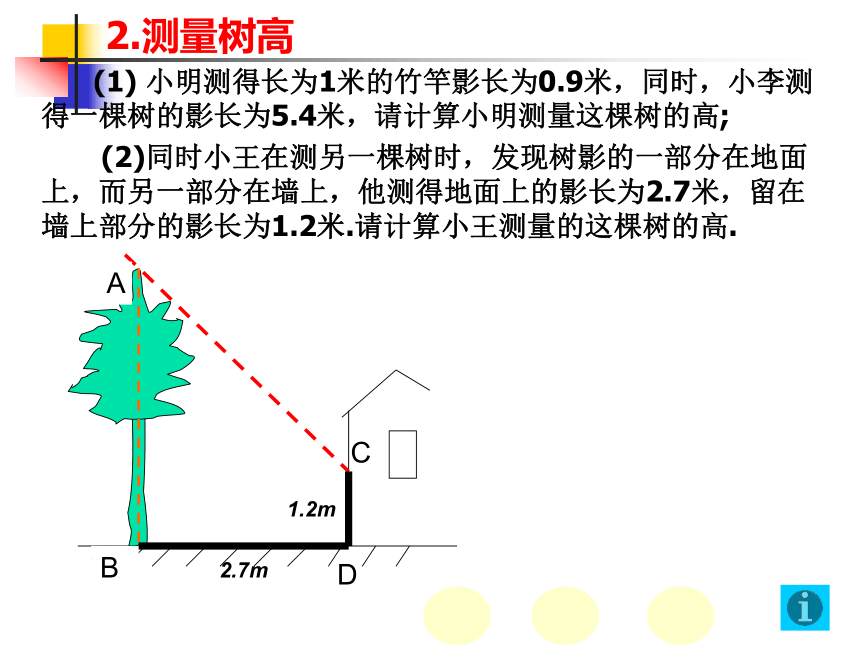
(1) 小明测得长为1米的竹竿影长为0.9米，同时，小李测得一棵树的影长为5.4米，请计算小明测量这棵树的高;
(2)同时小王在测另一棵树时，发现树影的一部分在地面上，而另一部分在墙上，他测得地面上的影长为2.7米，留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
2.7m
1.2m
B
A
C
D
2.测量树高
(1) 小明测得长为1米的竹竿影长为0.9米，同时，小李测得一棵树的影长为5.4米，请计算小明测量这棵树的高;
(2)同时小王在测另一棵树时，发现树影的一部分在地面上，而另一部分在墙上，他测得地面上的影长为2.7米，留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
2.7m
1.2m
B
A
C
解:画CG⊥AB于G， CG=BD=2.7，BD=CD=1.2
答:这棵树的高为4.2米.
D
G
由相似三角形的性质得: AG:CG=1:0.9 ∴AG=2.7÷0.9=3 AB=AG+BG=4.2
2.测量树高
由相似三角形的性质得: BE 1
2.7 0.9
(1) 小明测得长为1米的竹竿影长为0.9米，同时，小李测得一棵树的影长为5.4米，请计算小明测量这棵树的高;
(2)同时小王在测另一棵树时，发现树影的一部分在地面上，而另一部分在墙上，他测得地面上的影长为2.7米，留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
2.7m
1.2m
解：如图，过点D画DE∥AC交AB于E点，由平行四边形ACDE得AE=CD=1.2，
B
A
D
C
E
∴BE=3，AB=BE+AE=4.2 答:这棵树高有4.2米.
2.测量树高
(1) 小明测得长为1米的竹竿影长为0.9米，同时，小李测得一棵树的影长为5.4米，请计算小明测量这棵树的高;
(2)同时小王在测另一棵树时，发现树影的一部分在地面上，而另一部分在墙上，他测得地面上的影长为2.7米，留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.
2.7m
1.2m
B
A
C
解:延长AC交BD延长线于G， 由相似三角形的性质得: CD:DG=1:0.9 ∴DG=0.9CD=1.08 BG=BD+DG=3.78
由CD:AB=DG:BG 得 AB=4.2 答:这棵树的高为4.2米.
D
G
2.测量树高
(3) 小明﹑小李二位同学再想利用树影测量树高.
小明测得长为1米的竹竿影长为2米，同时，小李测量一棵树时发现树影的一部分在地面上，另一部分在斜坡的坡面上，测得在地面影长为10米，在斜坡上影长为4米，斜坡的倾斜角为30°，请计算这棵树的高．
10m
B
A
C
D
4m
30°
2.测量树高
(3) 小明测得长为1米的竹竿影长为2米，同时，小李测量一棵树时发现树影的一部分在地面上，另一部分在斜坡的坡面上，测得在地面影长为10米，在斜坡上影长为4米，斜坡的倾斜角为30°，请计算这棵树的高．
10m
B
A
C
解:画CG⊥AB于G点，画CE ⊥BD于E，则
CE= CD=2， DE=2
∴BG=CE=2， BE=BD+DE=10+2
答:这棵树的高为(7+ )米.
D
G
由相似三角形的性质得: AG:GC=1:2 ∴AG=5+ AB=BG+AG=7+
4m
E
30°
2.测量树高
(3) 小明测得长为1米的竹竿影长为2米，同时，小李测量一棵树时发现树影的一部分在地面上，另一部分在斜坡的坡面上，测得在地面影长为10米，在斜坡上影长为4米，斜坡的倾斜角为30°，请计算这棵树的高．
10m
B
A
C
D
G
4m
E
30°
2.测量树高
(3)小明测得长为1米的竹竿影长为2米，同时，小李测量一棵树时发现树影的一部分在地面上，另一部分在斜坡的坡面上，测得在地面影长为10米，在斜坡上影长为4米，斜坡的倾斜角为30°，请计算这棵树的高．
10m
B
A
C
D
4m
E
F
30°
2.测量树高
(3)小明测得长为1米的竹竿影长为2米，同时，小李测量一棵树时发现树影的一部分在地面上，另一部分在斜坡的坡面上，测得在地面影长为10米，在斜坡上影长为4米，斜坡的倾斜角为30°，请计算这棵树的高．
10m
B
A
C
D
G
4m
E
F
30°
2.测量树高
2.测量树高
小明﹑小李﹑小王三位同学想利用树影测量树高．
　 (1) 小明测得长为1米的竹竿影长为0.9米，同时，小李测得一棵树的影长为5.4米，请计算小明测量这棵树的高．
5.4
0.9
1
小结:
实际问题
数学问题
数学问题的解
检验
1、
2、 数学思想方法: 化归思想
思考题：镜子问题
　　　(1)一面镜子垂直地面放置于墙壁上，平常的镜子较大能看到自己的全身像，现在想把镜子高度缩小，但要求能看到全身像，问能否求出镜子上下边之间的最小高度？
(2)当镜子的高度取到最小值时，镜子下边挂在离地面多高的位置时，恰好能看到自己的全身像？
A
B
C
D
E
M
N
P
Q
C`
F
镜面
人
像
(1)镜面的最小高度是
1 PQ= AB 2
(2)镜面的下边离地面的距离是: 1 QN= CB 2
小结：
１、通过这节课的学习，让我们体验到数学就在我们身边；
２、解决实际问题时，首先应该从数学角度去思考，从而转化为数学问题；
３、化归思想是数学中常用的思想方法；
４、通过构造三角形，利用相似三角形的性质是求线段长度的常用方法。 ?v