相似三角形的判定及性质[下学期]

课件15张PPT。三角形相似判定及其性质第七单元 第二课时：
1.本课时的重点是相似三角形的判定.2.相似三角形的定义：对应角相等，对应边成比例的三角形.3.相似三角形的判定定理及其推论
判定定理1：两角对应相等的两个三角形相似.
判定定理2：两边对应成比例且夹角相等，两个三角形相似.
判定定理3：三边对应成比例的两个三角形相似
判定定理4：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似.一、知识要点4.相似三角形的性质
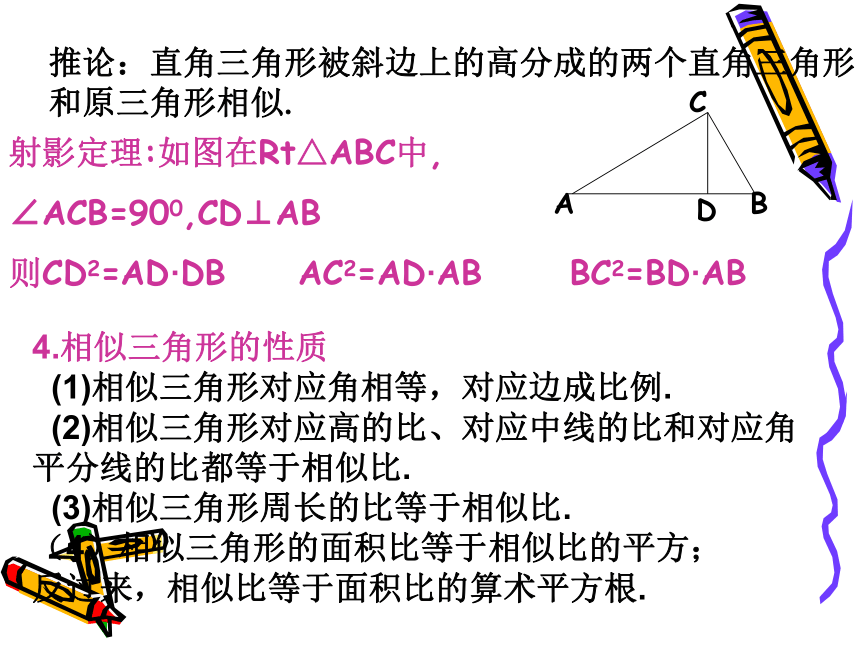
(1)相似三角形对应角相等，对应边成比例.
(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(3)相似三角形周长的比等于相似比.
（4）相似三角形的面积比等于相似比的平方；
反过来，相似比等于面积比的算术平方根.推论：直角三角形被斜边上的高分成的两个直角三角形
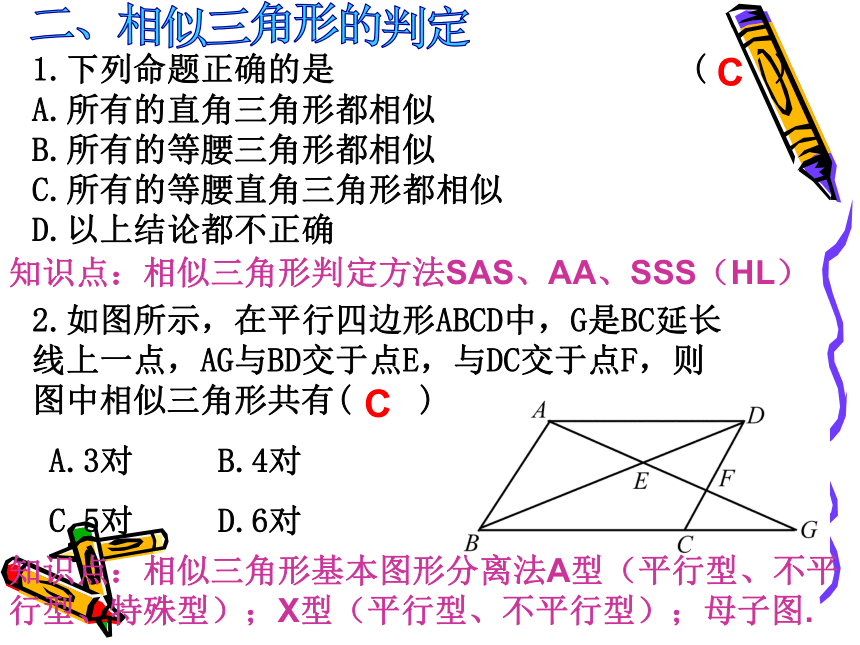
和原三角形相似.B2.如图所示，在平行四边形ABCD中，G是BC延长线上一点，AG与BD交于点E，与DC交于点F，则图中相似三角形共有( )
A.3对 B.4对
C.5对 D.6对1.下列命题正确的是 ( )
A.所有的直角三角形都相似
B.所有的等腰三角形都相似
C.所有的等腰直角三角形都相似
D.以上结论都不正确
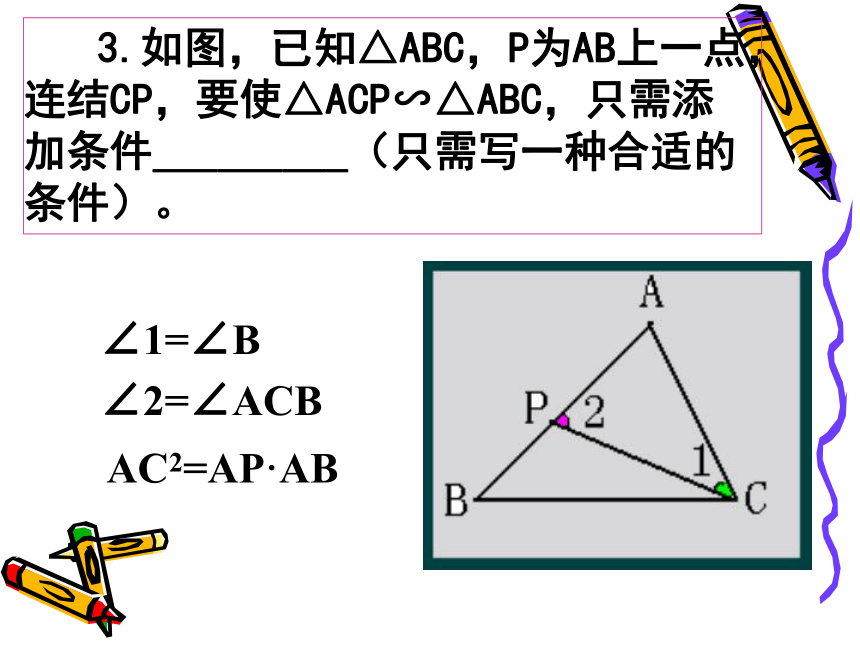
CC二、相似三角形的判定知识点：相似三角形判定方法SAS、AA、SSS（HL）知识点：相似三角形基本图形分离法A型（平行型、不平行型、特殊型）；X型（平行型、不平行型）；母子图. 3.如图，已知△ABC，P为AB上一点，连结CP，要使△ACP∽△ABC，只需添加条件_________（只需写一种合适的条件）。∠1=∠B
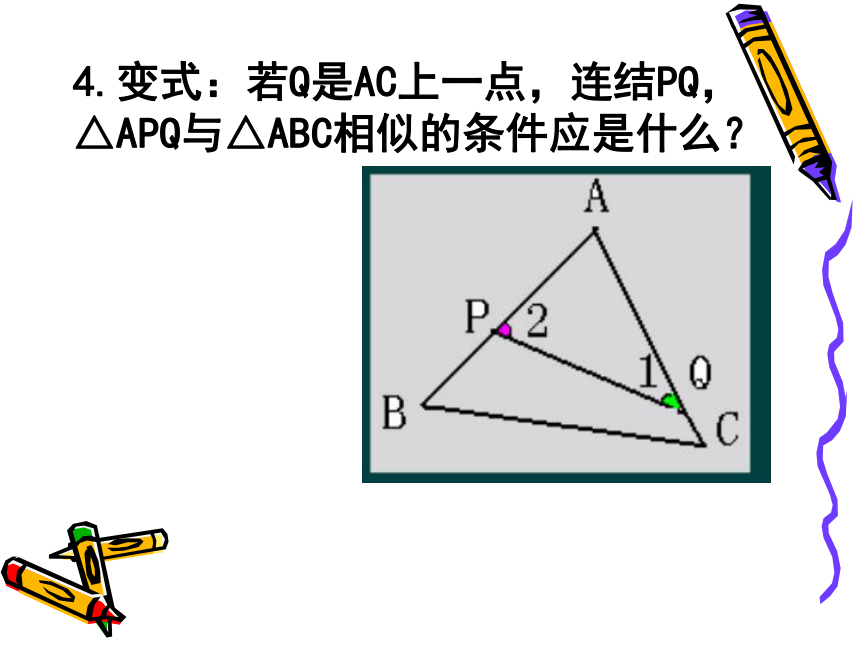
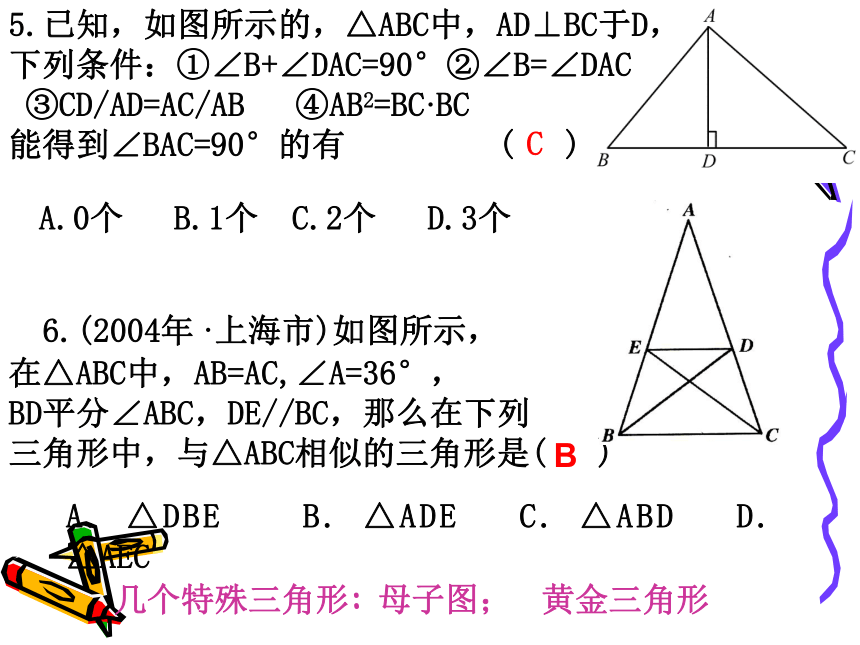
∠2=∠ACBAC2=AP·AB4.变式：若Q是AC上一点，连结PQ，△APQ与△ABC相似的条件应是什么？5.已知，如图所示的，△ABC中，AD⊥BC于D，
下列条件：①∠B+∠DAC=90°②∠B=∠DAC
③CD/AD=AC/AB ④AB2=BC·BC
能得到∠BAC=90°的有 ( ) A.0个 B.1个 C.2个 D.3个 C
6.(2004年·上海市)如图所示，
在△ABC中，AB=AC,∠A=36°，
BD平分∠ABC，DE//BC，那么在下列
三角形中，与△ABC相似的三角形是( )B几个特殊三角形: 母子图； 黄金三角形A. △DBE B. △ADE C. △ABD D. △AEC 8.如图所示，要判定△ABC的面积是△PBC面积的几倍，只用一把仅有刻度的直尺，需要度量的次数最少是
( )
A.3次 B.2次 C.1次 D.3次以上 C【解析】这道题乍一看，认为同底，只要知道高之比，就知道面积之比，故选B，其实不然，只要过AP量一次，连接AP并延长交BC于D，DP与AD的比就等于△PBC与△ABC的面积比，理由是：分别过A、P作BC的垂线段，根据两三角形相似的性质知：DP/AD=PE/AF.所以正确的答案是C.7.△ABC中，AC=6，BC=4，CA=9，△ABC∽△A′B′C′，△A′B′C′最短为12，则它的最长边的长度为( ) A.16 B.18 C.27 D.24 C三、相似三角形性质9. (1) 如图,在Rt△ABC中,∠C=900,
CD⊥AB,垂足为D,AD=8,DB=2,
则CD的长为 ( )
A. 4 B. 16 C. D.
(2)直角三角形的两条直角边长之比为1∶2,则它们在斜边上的射影之比是( )
A. 1∶2 B. 1∶ C. 1∶4 D. 1∶(3)把Rt△ABC斜边所在直线上满足 PC2=PA·PB的点P染上红色,则最多有红点的个数为 ( )
A. 1个 B. 2个 C. 3个 D.4个BCADC知识点:射影定理(4)女孩子都爱美,你知道穿鞋跟多高的鞋子看起来最美吗?只要当人的下肢与身高的比例成黄金分割,即下肢与身高之比为0.618时看起来最美,请你计算,一个身高为168cm,下肢长为102cm的女模特,应穿鞋跟高约为( )cm的高跟鞋显得比较美.
A.1.8 B. 2.8 C.3.8 D.4.810．(2004·西宁)如图，正方形ABCD边长是2，
BE＝CE,MN=1,线段MN的两端在CD、AD上滑动，
当DM= 时， △ABE与
以D、M、N为顶点的三角形相似。11.如图，ABCD是面积为a2的任意四边形，
顺次连接各边中点得四边形A1B1C1D1，
再顺次连接A1B1C1D1得到四边形A2B2C2D2，
重复同样的方法直到得到四边形AnBnCnDn，
则四边形AnBnCnDn的面积为 。四、格点三角形12.在大小为4×4的正方形格中,如右图所示,△ABC的顶点为A、B、C,在单位正方形的顶点上,请在图中分别画出4个不同大小的△A1B1C1,使△ ABC∽ △ A1B1C1(相似比不为1),且点A1、B1、C1都在单位正方形的顶点上.13.如下图所示,在正方形网格中,小格的顶点叫做格点.小华按下列要求作图:(1)在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;(2)连结三个格点,使之构成直角三角形.小华在左边的正方形网格中作出了△ABC.请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等.五、一个特殊图形（三垂图）14.已知如图,梯形ABCD中,AD∥BC,∠A=900,AD=3,BC=8,AB=10,问在AB上是否存在点P,使△APD和△BPC相似?如果存在,请确定P点位置(用AP的长表示);如果不存在,说明理由.点拨:利用相似三角形的对应边成比例性质即可探求结论,在探索过程中,应考虑Rt△APD和Rt△BPC的不同位置的对应.感悟:探索性试题是中考的热点,培养学生的探究能力和实践能力,复习时需加强这方面的训练.拓展:在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角尺的直角顶点与点P重合,并且一条直角边始终经过点B,另一条直角边与正方形的某一边所在直线交于点E.
探究：（1）观察操作结果，哪一个三角形与△BDC相似？并证明你的结论；（2）当点P位于CD的中点时，你找到的三角形与△BPC的周长比是多少？六、相似形与二次函数综合15.已知抛物线y=ax2+bx+c的顶点坐标为(4 , -1),与y交于点C(0 ,3),O是原点.
(1)求这条抛物线的解析式;
(2)设此抛物线与x轴的交点为A、B(A在B的左边),问在y轴上是否存在点P使以O、B、P为顶点的三角形与△AOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.七、反思与总结反思为了更加完善
总结为了更好提高作业：精析巧练P115-117 、 P123-124 再见！