4.4相似三角形性质的应用(3)[下学期]
文档属性
| 名称 | 4.4相似三角形性质的应用(3)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 591.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-03 09:34:00 | ||
图片预览


文档简介
课件19张PPT。三角形相似的应用第七单元 第三课时:
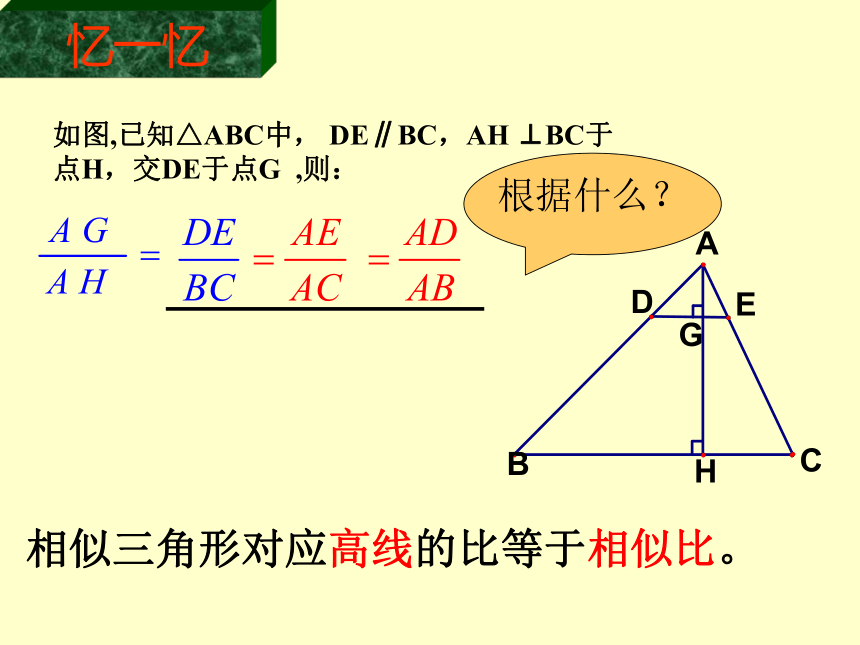
如图,已知△ABC中, DE∥BC,AH ⊥BC于点H,交DE于点G ,则:
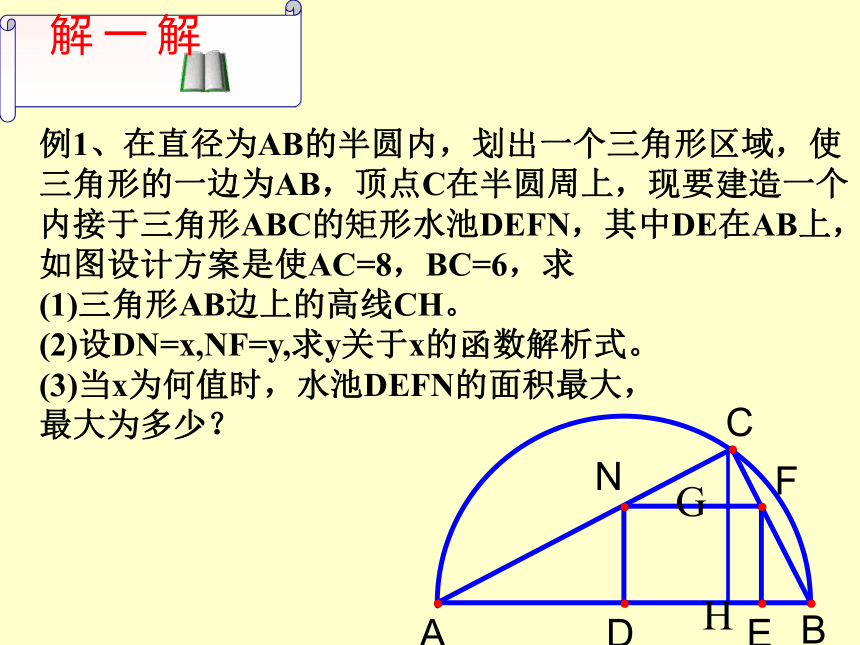
忆一忆根据什么?相似三角形对应高线的比等于相似比。例1、在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,求
(1)三角形AB边上的高线CH。
(2)设DN=x,NF=y,求y关于x的函数解析式。
(3)当x为何值时,水池DEFN的面积最大,
最大为多少?
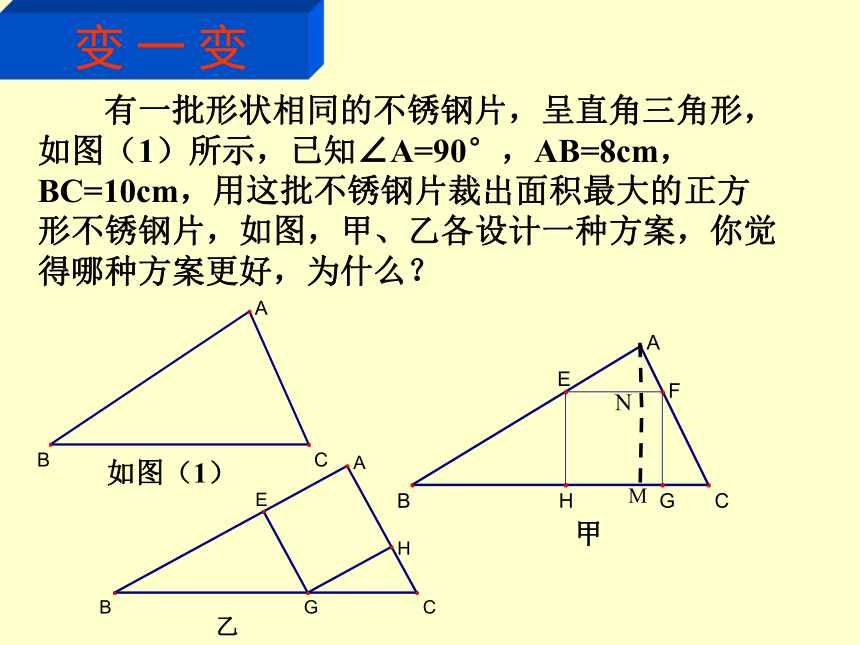
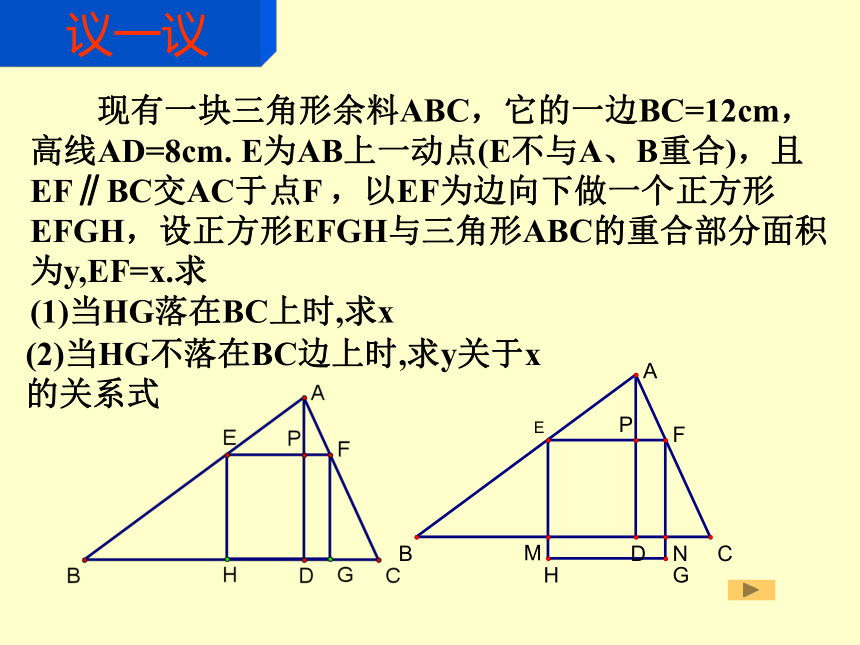
HG 有一批形状相同的不锈钢片,呈直角三角形,如图(1)所示,已知∠A=90°,AB=8cm,BC=10cm,用这批不锈钢片裁出面积最大的正方形不锈钢片,如图,甲、乙各设计一种方案,你觉得哪种方案更好,为什么?如图(1)甲乙 变 一 变MN 现有一块三角形余料ABC,它的一边BC=12cm,高线AD=8cm. E为AB上一动点(E不与A、B重合),且EF∥BC交AC于点F ,以EF为边向下做一个正方形EFGH,设正方形EFGH与三角形ABC的重合部分面积为y,EF=x.求
(1)当HG落在BC上时,求x
议一议(2)当HG不落在BC边上时,求y关于x的关系式
解题小结一个基本图形。在复习相似三角形的过程中,我们可以把一些基本图形归类,熟记一些基本的方法,都将帮助我们解题。以相似三角形 背景的综合题,要充分运用方程、分类讨论、转化、函数以及数形结合的思想来研究解决。 在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,求(1)三角形AB边上的高线CH
(2)设DN=x,NF=y,求y关于x的函数解析式
(3)当x为何值时,水池DEFN的面积最大,最大为多少?
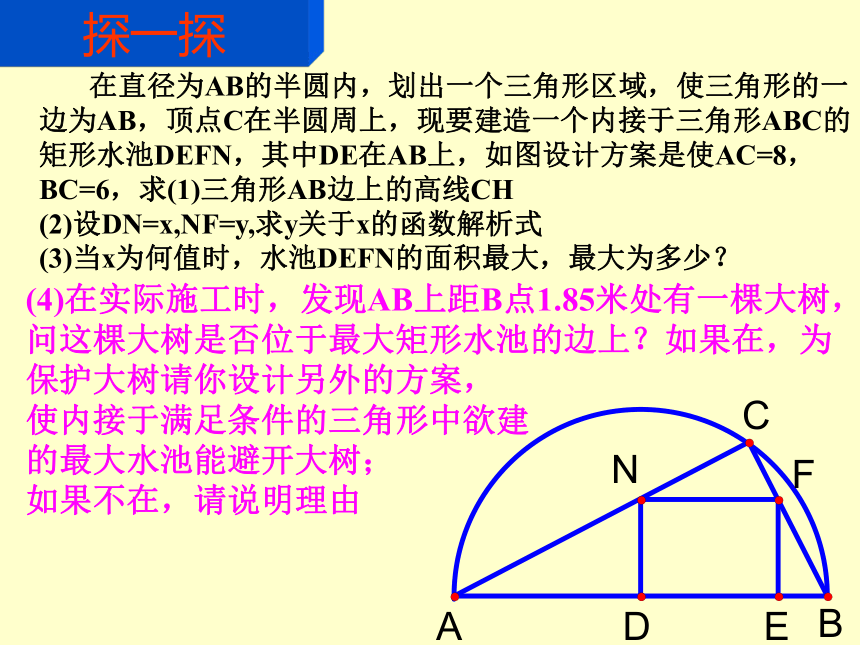
探一探(4)在实际施工时,发现AB上距B点1.85米处有一棵大树,问这棵大树是否位于最大矩形水池的边上?如果在,为保护大树请你设计另外的方案,
使内接于满足条件的三角形中欲建
的最大水池能避开大树;
如果不在,请说明理由
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(1)如图1,四边形DEFG为⊿ABC的内接正方形,求正方形的边长。
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接与⊿ABC,求正方形的边长(1)如图1,四边形DEFG为⊿ABC的内接正方形,求正方形的边长。
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(3)如图3,三角形内有并排的三个相等的正方形,它们组成的矩形内接于⊿ABC,求正方形的边长。(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接与⊿ABC,求正方形的边长(1)如图1,四边形DEFG为⊿ABC的内接正方形,求正方形的边长。
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(4)如图4,三角形内有并排的个正方形,它们组成的矩形内节于⊿ABC,请写出正方形的边长。 1.(2004.江苏无锡市)已知,如图所示的四边形ABCD为菱形,AF⊥BC于F,
(1)求证:AD2= DE·DB.
(2)过点E作EG⊥AF交AB于点G,若线段BE,DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为 ,求EG的长.【解析】(1)证等积式,首先想到化成比例式,但式子有12,应想到菱形的性质:对角线互相垂直平分,故连接AC交BD于O点,即BD=2DO,所以AD2=DE·DO 做一做 2.(2005·山东省)如图中的(1)是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1,BE交于点M、N,且图(1)被直线MN分成面积相等的上、下两部分.
(1)求 的值.(2)求MB、NB的长.
(3)将图(1)沿虚线折成一个无盖的正方体纸盒(如图(2)所示)后,求点M、N间的距离. 图(1) 图(2) M(2)∵分成的两部分面积相等得MB·NB= ,即
MB·NB=5 MB+NB=5,因此可以构造一元二次
方程x2-5x+5=0,且MB<NB.
∴MB= ,NB= (3)由(2)已知B1M= ∵图(2)中的BN与图(1)中的EN相等.
∴BN=B1M,
即四边形BB1MN是矩形.∴MN=1. 3.如图所示,梯形ABCD中,AB∥CD,∠B=90°,
MN∥AB,AB=6,BC=4,CD=3,设DM=x.(1)设MN=y,用x的代数式表示y.
(2)设梯形MNCD的面积为S,用x
的代数式表示S.
(3)若梯形MNCD的面积S等于梯
形ABCD的面积的13,求DM.
【解析】(1)过D作DE⊥AB于E点交MN于F,MN=MF+FN=MF+3,在Rt△DAE中,AD= 由MN∥AB 同学们,本节课你又有哪些收获? 说一说谢谢
如图,已知△ABC中, DE∥BC,AH ⊥BC于点H,交DE于点G ,则:
忆一忆根据什么?相似三角形对应高线的比等于相似比。例1、在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,求
(1)三角形AB边上的高线CH。
(2)设DN=x,NF=y,求y关于x的函数解析式。
(3)当x为何值时,水池DEFN的面积最大,
最大为多少?
HG 有一批形状相同的不锈钢片,呈直角三角形,如图(1)所示,已知∠A=90°,AB=8cm,BC=10cm,用这批不锈钢片裁出面积最大的正方形不锈钢片,如图,甲、乙各设计一种方案,你觉得哪种方案更好,为什么?如图(1)甲乙 变 一 变MN 现有一块三角形余料ABC,它的一边BC=12cm,高线AD=8cm. E为AB上一动点(E不与A、B重合),且EF∥BC交AC于点F ,以EF为边向下做一个正方形EFGH,设正方形EFGH与三角形ABC的重合部分面积为y,EF=x.求
(1)当HG落在BC上时,求x
议一议(2)当HG不落在BC边上时,求y关于x的关系式
解题小结一个基本图形。在复习相似三角形的过程中,我们可以把一些基本图形归类,熟记一些基本的方法,都将帮助我们解题。以相似三角形 背景的综合题,要充分运用方程、分类讨论、转化、函数以及数形结合的思想来研究解决。 在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,求(1)三角形AB边上的高线CH
(2)设DN=x,NF=y,求y关于x的函数解析式
(3)当x为何值时,水池DEFN的面积最大,最大为多少?
探一探(4)在实际施工时,发现AB上距B点1.85米处有一棵大树,问这棵大树是否位于最大矩形水池的边上?如果在,为保护大树请你设计另外的方案,
使内接于满足条件的三角形中欲建
的最大水池能避开大树;
如果不在,请说明理由
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(1)如图1,四边形DEFG为⊿ABC的内接正方形,求正方形的边长。
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接与⊿ABC,求正方形的边长(1)如图1,四边形DEFG为⊿ABC的内接正方形,求正方形的边长。
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(3)如图3,三角形内有并排的三个相等的正方形,它们组成的矩形内接于⊿ABC,求正方形的边长。(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接与⊿ABC,求正方形的边长(1)如图1,四边形DEFG为⊿ABC的内接正方形,求正方形的边长。
练习(2003,潍坊)在Rt⊿ABC中,
∠C=90。,AC=4,BC=3,(4)如图4,三角形内有并排的个正方形,它们组成的矩形内节于⊿ABC,请写出正方形的边长。 1.(2004.江苏无锡市)已知,如图所示的四边形ABCD为菱形,AF⊥BC于F,
(1)求证:AD2= DE·DB.
(2)过点E作EG⊥AF交AB于点G,若线段BE,DE(BE<DE)的长是方程x2-3mx+2m2=0(m>0)的两个根,且菱形ABCD的面积为 ,求EG的长.【解析】(1)证等积式,首先想到化成比例式,但式子有12,应想到菱形的性质:对角线互相垂直平分,故连接AC交BD于O点,即BD=2DO,所以AD2=DE·DO 做一做 2.(2005·山东省)如图中的(1)是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1,BE交于点M、N,且图(1)被直线MN分成面积相等的上、下两部分.
(1)求 的值.(2)求MB、NB的长.
(3)将图(1)沿虚线折成一个无盖的正方体纸盒(如图(2)所示)后,求点M、N间的距离. 图(1) 图(2) M(2)∵分成的两部分面积相等得MB·NB= ,即
MB·NB=5 MB+NB=5,因此可以构造一元二次
方程x2-5x+5=0,且MB<NB.
∴MB= ,NB= (3)由(2)已知B1M= ∵图(2)中的BN与图(1)中的EN相等.
∴BN=B1M,
即四边形BB1MN是矩形.∴MN=1. 3.如图所示,梯形ABCD中,AB∥CD,∠B=90°,
MN∥AB,AB=6,BC=4,CD=3,设DM=x.(1)设MN=y,用x的代数式表示y.
(2)设梯形MNCD的面积为S,用x
的代数式表示S.
(3)若梯形MNCD的面积S等于梯
形ABCD的面积的13,求DM.
【解析】(1)过D作DE⊥AB于E点交MN于F,MN=MF+FN=MF+3,在Rt△DAE中,AD= 由MN∥AB 同学们,本节课你又有哪些收获? 说一说谢谢
同课章节目录
