2.1 等腰三角形[上学期]

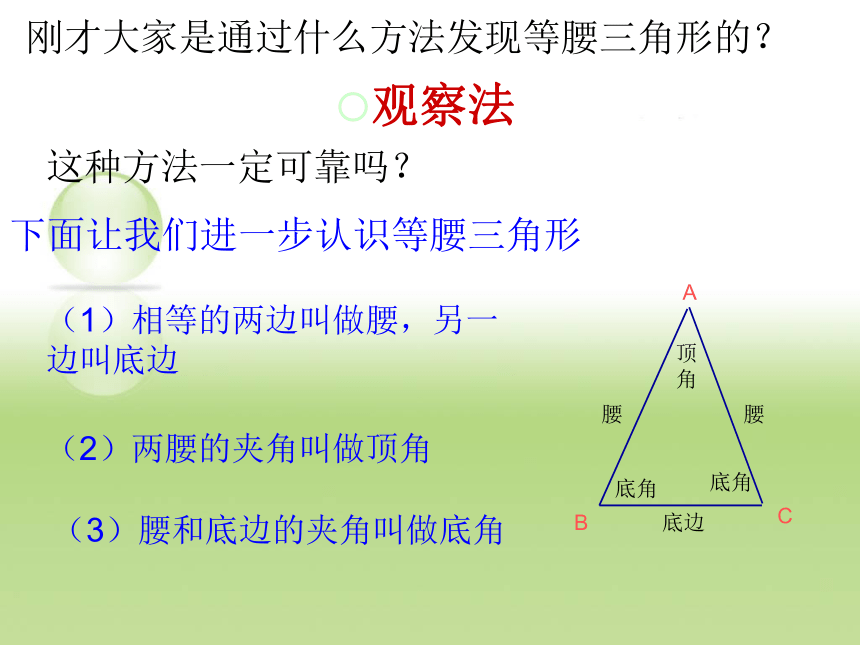
课件12张PPT。从这些图片中你是否发现有三角形你觉得这些三角形的形状特殊吗？它们有两边相等定义：有两边相等的三角形叫做等腰三角形刚才大家是通过什么方法发现等腰三角形的？观察法这种方法一定可靠吗？下面让我们进一步认识等腰三角形ABC底边顶角腰腰底角底角（1）相等的两边叫做腰，另一　　　　　　　　　边叫底边（2）两腰的夹角叫做顶角（3）腰和底边的夹角叫做底角不一定2.1 等腰三角形本课是对过去所学知识的复习，又是对你新的挑战！
你准备好了吗？新课就要开始啦！文成二中　　　赵东贵挑战一：请你做一做1、课本做一做第1题
答：有2个等腰三角形，即△ABD， △ABC
2、课本做一做第2题
作法：
（1）作线段BD＝a；
（2）分别以B、C为圆心，线段b为半径作弧，相交于点A；
（3）连结AB，AC。
　　△ABC就是所求的三角形。下面让我们动动手吧，记住别忘了动脑哦！问题：在等腰三角形纸片画出顶角平分线，然后沿着顶角平分线对折，你发现了什么？由此你能得出什么结论？ 结论：等腰三角形是轴对称图形，顶角平
分线是它的对称轴。现在是学习例题时间，要好好学。 例 如图，在△ABC中，AB=AC，D，E分别是AB，AC上的点，且AD=AE。AP是△ABC的角平分线。点D，E关于AP对称吗？DE与BC平行吗？请说明理由。例 如图，在△ABC中，AB=AC，D，E分别是AB，AC上的点，且AD=AE。AP是△ABC的角平分线。点D，F关于AP对称吗？DE与BC平行吗？请说明理由。解：点D，E关于AP对称，且DE∥BC。
理由如下：因为AP是∠ABC的平分线，AB＝AC，AD＝AE，则当把图形沿直线AP对折时，线段AB与AC重合，线段AD与AE重合，所以点B，C关于直线AP对称，点D，E也关于直线AP对称，所以BC⊥AP，DE⊥AP，所以DE∥BC。知识只有亲自经历才能掌握，请认真做好以下练习：1 .“课内练习”第一题.
2.“课内练习”第二题. 下面我们来动手操作，探索规律，OK？在平面内，分别用3根、5根、6根火柴棒首尾顺次相接，能搭成什么形状的三角形？通过尝试，完成下面的表格。7根火柴棒呢？8根呢？9根呢？你发现什么规律？等边
三角形等腰三角形接下来谈谈体验吧！1.在本节课的学习中，你有那些收获？
2.你对那一点最感兴趣？
3.你还有那些新的发现？ 1、了解等腰三角形的概念，能识别腰、底边、顶角、底角。
2、掌握等腰三角形顶角平分线所在的直线是它的对称轴。
3、会运用概念和轴对称性解决简单几何问题。认真作业对于学习很重要！1、作业本
2、课本作业题
3、根据等腰三角形的轴对称性，你还能发现有关等腰三角形的哪些结论？与你的同伴交流。
如果时间允许的话，别忘了同步练习哦！下课了！好高兴呀！！