2022-2023学年浙教版八年级数学上册4.2平面直角坐标系 课件(共14张PPT)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册4.2平面直角坐标系 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
4.2 平面直角坐标系
同学们,你们知道这幅图描述的地点是在哪儿吗?
小Z同学每天早上从古塘丽景小区北门出发去古塘中学上学,他所走的路线是这样的:出小区门向左走30米,再右转向北走30米,
你能用有序数对描述校门的位置吗?
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
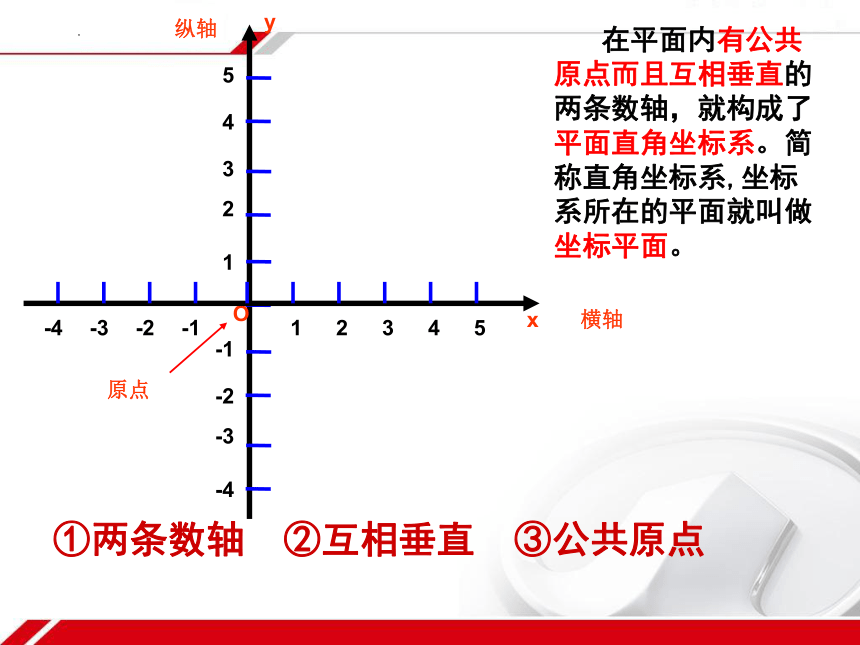
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系。简称直角坐标系,坐标系所在的平面就叫做坐标平面。
①两条数轴 ②互相垂直 ③公共原点
x
y
原点
第一象限
第四象限
第三象限
第二象限
注 意:坐标轴不属于任何象限。
o
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
(3,2)
·
C
(-4,1)
方法:先横后纵
B(2,3)
D
E
(-3,-3)
(5,-4)
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3, 2)
记作:A(3,2)
·
B
(-2,0)
(0,-2.5)
F
G
(0,0)
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y)和它对应。
这个有序实数对(x,y)就是这个点的坐标。
反之,对于任意一个有序数对(x,y),
都可以用平面内唯一的一个点来表示.
笛卡尔(1596-1660)
笛卡尔和直角坐标系
笛卡尔,法国数学家、科学家和哲学家。早在1637年以前,他受到了经纬度的启发。(地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上看可以看成平面内互相垂直的两条线.)发明了平面直角坐标系,又称笛卡尔坐标系。
例1(1)写出平面直角坐标系中点A、B、C、D、E的坐标
(2)在坐标系中画出以下点
(4,3.5)
(-4,-3)
(2,-1)
(-3,-4)
(0,-3)
观察你所求出的这些点的坐标,回答下列问题:
(1)这些点分别位于哪个象限或坐标轴
(-4,4.5)
(0,0)
(-5,0)
(0,2.5)
0 1 2 3 4 5 6
6
5
4
3
2
1
y
x
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
A
B
C
O
E
D
位于第一象限的点有D (4, 3.5)
位于第二象限的点有(-4, 4.5)
位于第三象限的点有A(-4,3)、B(-3,4)
位于第四象限的点有E(2, -1)
位于x轴的点有(-5, 0)和(0,0)
位于y轴的点有 (0, 2.5),C(0,-3)和(0,0)
第一象限
第四象限
第三象限
第二象限
归纳特征
(+,+)
(-,+)
(-,-)
(+,-)
点的位置
在第一象限
横坐标
符号
在第二象限
在第三象限
在第四象限
+
+
+
-
-
+
-
-
纵坐标
符号
探索:根据点所在的位置,用 “+” “-” 填空。
o
y
x
-4 -3 -2 -1 1 2 3 4
3
2
1
-1
-2
-3
(纵轴)
(横轴)
A
B
C
D
E
F
C (4 , 0)
A (- 3, 0)
B (1, 0)
D (0, 3 )
E (0 , 2)
F (0 , -2)
说一说
y 轴上的点的横坐标有什么特点
x 轴上的点的纵坐标有什么特点
x 轴上的点,纵坐标为0.
y轴上的点,横坐标为0.
记( X,0)
记( 0,y)
课内练习
如图
(1)写出图中六边形各个顶点的坐标,他们各在哪个象限内或坐标轴上,哪些点的横坐标相同,哪些点的纵坐标相同。
(2)作出点G(-2,-1),H(-3,5),M(0,3),N(5,-2),并判断这些点中哪些在六边形内,哪些在六边形外?
巩固练习
巩固练习
这节课我的收获是……
我还有哪些疑惑……
课堂小结
1.平面直角坐标系概念
O
y
x
(+,+)
(-,+)
(-,-)
(+,-)
x轴上的点,纵坐标为0,记(x,0);
y轴上的点,横坐标为0,记(0,y).
{
2.已知点写坐标;
3.已知坐标找点.
}
依据
4.2 平面直角坐标系
同学们,你们知道这幅图描述的地点是在哪儿吗?
小Z同学每天早上从古塘丽景小区北门出发去古塘中学上学,他所走的路线是这样的:出小区门向左走30米,再右转向北走30米,
你能用有序数对描述校门的位置吗?
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系。简称直角坐标系,坐标系所在的平面就叫做坐标平面。
①两条数轴 ②互相垂直 ③公共原点
x
y
原点
第一象限
第四象限
第三象限
第二象限
注 意:坐标轴不属于任何象限。
o
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
(3,2)
·
C
(-4,1)
方法:先横后纵
B(2,3)
D
E
(-3,-3)
(5,-4)
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3, 2)
记作:A(3,2)
·
B
(-2,0)
(0,-2.5)
F
G
(0,0)
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y)和它对应。
这个有序实数对(x,y)就是这个点的坐标。
反之,对于任意一个有序数对(x,y),
都可以用平面内唯一的一个点来表示.
笛卡尔(1596-1660)
笛卡尔和直角坐标系
笛卡尔,法国数学家、科学家和哲学家。早在1637年以前,他受到了经纬度的启发。(地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上看可以看成平面内互相垂直的两条线.)发明了平面直角坐标系,又称笛卡尔坐标系。
例1(1)写出平面直角坐标系中点A、B、C、D、E的坐标
(2)在坐标系中画出以下点
(4,3.5)
(-4,-3)
(2,-1)
(-3,-4)
(0,-3)
观察你所求出的这些点的坐标,回答下列问题:
(1)这些点分别位于哪个象限或坐标轴
(-4,4.5)
(0,0)
(-5,0)
(0,2.5)
0 1 2 3 4 5 6
6
5
4
3
2
1
y
x
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
A
B
C
O
E
D
位于第一象限的点有D (4, 3.5)
位于第二象限的点有(-4, 4.5)
位于第三象限的点有A(-4,3)、B(-3,4)
位于第四象限的点有E(2, -1)
位于x轴的点有(-5, 0)和(0,0)
位于y轴的点有 (0, 2.5),C(0,-3)和(0,0)
第一象限
第四象限
第三象限
第二象限
归纳特征
(+,+)
(-,+)
(-,-)
(+,-)
点的位置
在第一象限
横坐标
符号
在第二象限
在第三象限
在第四象限
+
+
+
-
-
+
-
-
纵坐标
符号
探索:根据点所在的位置,用 “+” “-” 填空。
o
y
x
-4 -3 -2 -1 1 2 3 4
3
2
1
-1
-2
-3
(纵轴)
(横轴)
A
B
C
D
E
F
C (4 , 0)
A (- 3, 0)
B (1, 0)
D (0, 3 )
E (0 , 2)
F (0 , -2)
说一说
y 轴上的点的横坐标有什么特点
x 轴上的点的纵坐标有什么特点
x 轴上的点,纵坐标为0.
y轴上的点,横坐标为0.
记( X,0)
记( 0,y)
课内练习
如图
(1)写出图中六边形各个顶点的坐标,他们各在哪个象限内或坐标轴上,哪些点的横坐标相同,哪些点的纵坐标相同。
(2)作出点G(-2,-1),H(-3,5),M(0,3),N(5,-2),并判断这些点中哪些在六边形内,哪些在六边形外?
巩固练习
巩固练习
这节课我的收获是……
我还有哪些疑惑……
课堂小结
1.平面直角坐标系概念
O
y
x
(+,+)
(-,+)
(-,-)
(+,-)
x轴上的点,纵坐标为0,记(x,0);
y轴上的点,横坐标为0,记(0,y).
{
2.已知点写坐标;
3.已知坐标找点.
}
依据
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
