5.1认识不等式[上学期]

课件21张PPT。动脑一刻中山公园中山公园的票
价是：每人5元；一次购票满30张，每张票可少收1元。现在，我们班有27名学生去到公园游玩，班长准备好了零钱到售票处买27张票时，爱动脑筋的同学李敏喊住了，提议买30张票，有人说多买不是浪费吗？究竟提议对不对？是不是真的浪费？
谈谈你们的看法。买27张票，要付款买30张票，要付款显然 120<135我们不妨一起来算一算5×27＝135（元）4×30＝120（元）问题这就是说，买30张票比买27张票付款要少，表面上看是
“浪费”了3张票，而实际上节省了。
在实际生活中除了等量关系外，还存在着很多象上面这样的不等量关系，这节课我们要学习它！引入课题5.1 认识不等式
探究新知下列问题中的数量关系能
用等式表示吗？若不能,
应该用怎样的式子来表示?
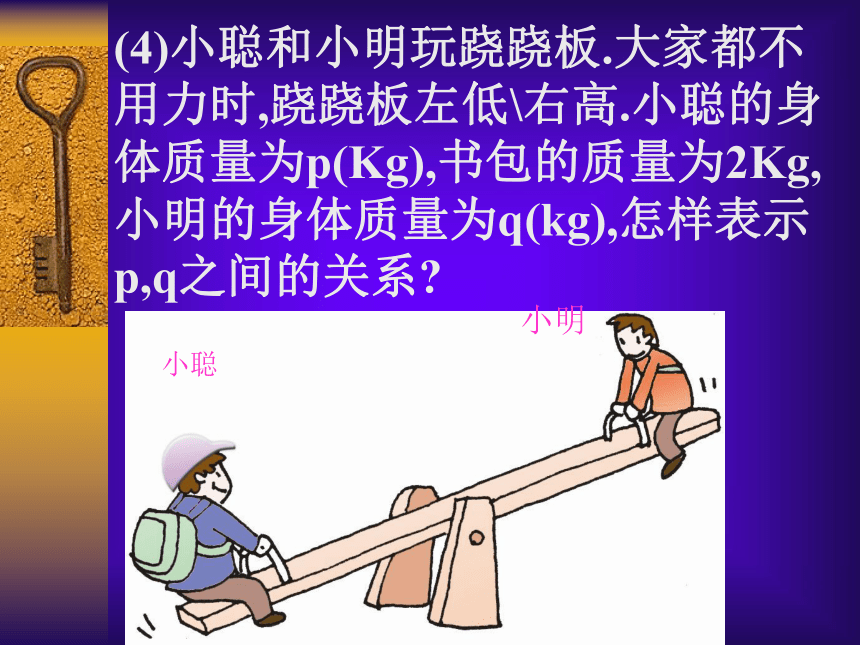
(1)公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(Km/h)表示汽车的速度,怎样表示v和40之间的关系?探究新知(2)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?(3)天平左盘放3个乒乓球,右盘放5克砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?(4)小聪和小明玩跷跷板.大家都不用力时,跷跷板左低右高.小聪的身体质量为p(Kg),书包的质量为2Kg,小明的身体质量为q(kg),怎样表示p,q之间的关系?小明小聪(5)要使代数式 有意义, x的值与3之间有什么关系?
观察由上述5个问题中得到的关系式，它们有什么共同的特点？
X＋3
X－3像上面出现的120<135,q+2>p，v≤40, t≥6000, x≠ 3这样，用符号“<”，（或“>”），“≤”（或 “≥”），“≠ ”连接而成的数学式子，叫做不等式（inequality）。“＞”“＜”“≥”“≤”“ ≠”这样的符号统称用不等号 练习1. P102概括例1:根据下列数量关系列不等式： （1）a是正数 ； （2）y的两倍与6的和比1小； （3）㎡减去10不大于10 （4）设a，b，c为一个三角形的三条边长，两边之和大于第三边解： (1) a>0(2) 2y+6<1(3) ㎡-10 ≤10
(4)a+b>c,,a+c>b,b+c>a练习：1、用不等式表示
（1） x与y的积是正数
（2） x的2.5倍小于-3
（3） 12与x 的2倍的差是正数
（4） t与6的和是非负数
（5） x、y两数的平方差不大于0
（6） y与1的差大于y的45%
（7） x比3小
（8） a不小于1
（9） y的绝对值与-8的和为正数
（10）a与b的差的平方是非负数 xy>0 2.5x<-3 12-2x>0t+6≥ 0 x2-y2≤ 0y-1>45%yx<3a≥ 1|y|-8>0(a-b)2≥ 0（1）已知x1=1,x2=2,请在数轴上表示出x1,x2的位置。（2）x＜1表示怎样的数的全体？做一做猜一猜：怎样在数轴上表示下列不等式： x＜a， x≥a， b＜x＜a（b＜a）x＜a表示小于a的全体实数，在数轴上表示a左边的所有点，不包括a在内（如图5—4） x≥a表示大于或等于a的全体实数，在数轴上表示a右边的所有点，包括a在内（如图5一5）； b＜x＜a（b＜a）表示大干b而小于a的全体实数，在数轴上表示如图5一6. 练习 P102， T3 例2 一座小水电站的水库水位在12~20m(包括12m,20m)时，发电机能正常工作。设水库水位为x(m) . 1、用不等式表示发电机正常工作的水位范围，并把它表示在数轴上； 2、当水位在下列位置时，发电机能正常工作吗? （1）x1=8（2）x2=10（3）x3=15（4）x4=19填空
(1)小于4的正整数有（ ），
不大于3的非负整数有（ ），
绝对值小于3的负整数有（ ）；
(2)若x<1，则-2x+2 01、2、30、1、2、3-1、-2>今天的收获有哪些呢？
今天我们初步认识了不等式，用不等号
“<”或“>”表示不等关系的式子，叫做不等
式。也可以用“≤”、“ ≥ ”、“≠ ”连接，
在表示数量关系时，一定要注意“负数”、
“非负数”、“大于”、“小于”、“不小于”等
关键
性词语，只有真正理解其含义，才能正确列
出不等式。作业
1.见作业本。

2.课本P103 谢谢