一元一次不等式的基本性质[上学期]

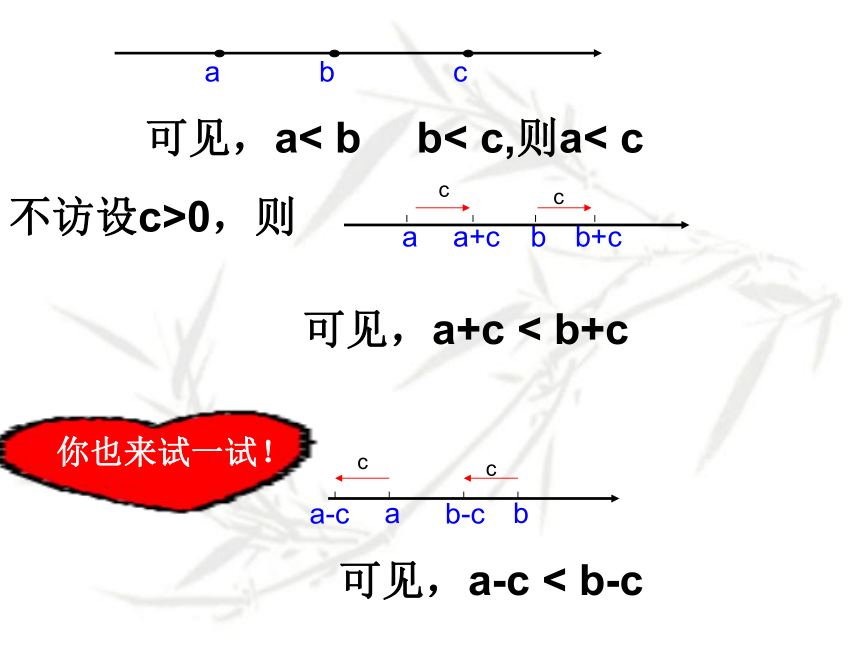
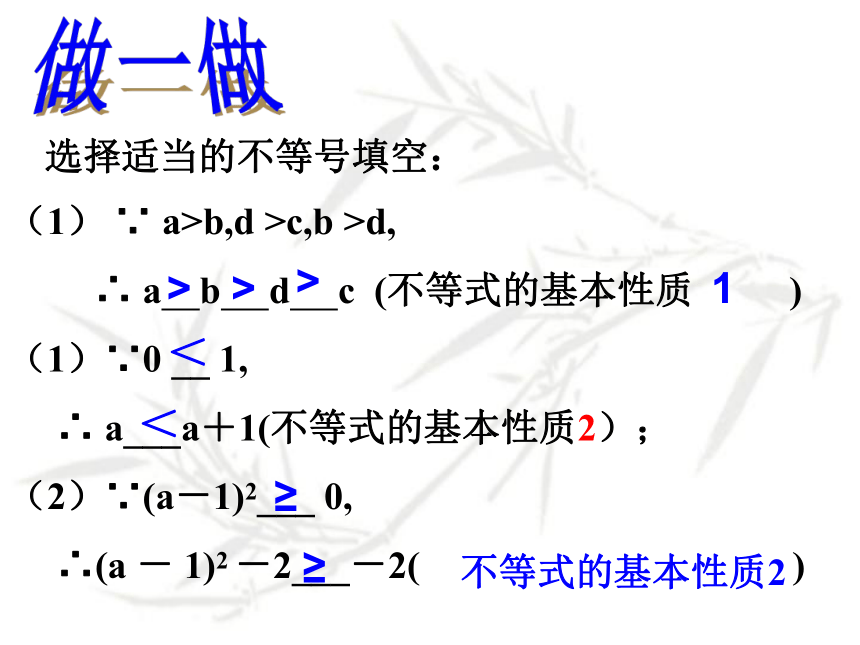
课件17张PPT。5.2不等式的基本性质执教者：何晓英[活动一]请你来帮忙不等式性质1：若a如果a>b，那么a+c>b+c; a-c>b-c以上性质能否用数轴来加以解释呢？abc不访设c>0，则a+cb+c可见，a+c < b+c可见，a-c < b-c你也来试一试！可见，a< b　 b< c,则a< c做一做选择适当的不等号填空：（1） ∵ a>b,d >c,b >d,
∴ a b d c (不等式的基本性质 )
（1）∵0 __ 1,
　∴ a___a＋1(不等式的基本性质2）；
（2）∵(a－1)2___ 0,
　∴(a － 1)2 －2___－2( )＜＜≥≥不等式的基本性质2>>>1[活动二]小军将不等式a ＜ 0进行了如下的变形，
两边都加上a，a+a ＜ a，即2a ＜a
两边都除以a,得2 ＜ 1，
2怎么会小于１呢？
小军可糊涂了……
聪明的同学，这究竟是怎么回事呢？
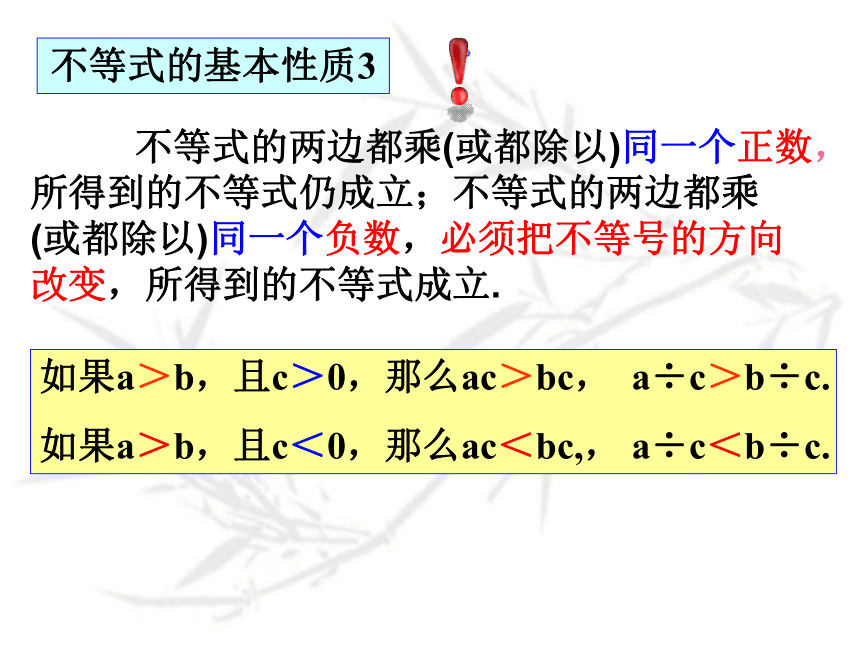
你能尝试着举几个例子吗？有什么结论？ 不等式的两边都乘(或都除以)同一个正数，所得到的不等式仍成立；不等式的两边都乘(或都除以)同一个负数，必须把不等号的方向改变，所得到的不等式成立.如果a＞b，且c＞0，那么ac＞bc， a÷c＞b÷c.
如果a＞b，且c＜0，那么ac＜bc,， a÷c＜b÷c.不等式的基本性质3做一做选择适当的不等号填空：(1)若x+1＞0，两边同加上－1，得____________
(依据:_____________________).
(2)若2x＞－6，两边同除以2，得___________，依据____________________.
(3)若－0.5 x≤1，两边同乘以－2，得________,依据__________________x ＞－1不等式的基本性质2x ＞－3不等式的基本性质3x≥－2不等式的基本性质3例　已知m<0 ，试比较2m与m的大小。解法一：∵ 2＞1，m＜0，
∴ 2m＜m（不等式的基本性质3）解法二：在数轴上分别表示2m和m的点（m＜0），如图.2m位于m的左边，所以2m＜m想一想：还有其他比较2m与m的大小的方法吗？∵ 2m－m=m，又∵ m＜0,
∴ 2m－m＜0,
∴2m-b,则a+b 0;
(2)若-a(3)若-a >-b,则2-a 2-b;
(4)若a(5)若a >0,且(1－b)a <0,则b 1;
相信自己是最棒的！拓展应用　　我国于2001年12月11日正式加入世界贸易组织（WTO）。加入前，产品A的进口税超过产品B的进口税的1倍以上；加入后，这两种产品的进口税都下调了15%。你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗？请说明理由。　 解：　设加入前产品A，B的进口税分别为a美元，b美元。由题意，得，a>2b。加入后A，B两种产品的进口税分别为(1－15%)a，(1－15%)b.由不等式的基本性质3，
∵ a>2b 　1－15%＞0
∴(1－15%)a＞2(1－15%)b
即表示产品A的进口税仍超过产品B的进口税的1倍以上感悟与反思小结一本节重点（1）掌握不等式的三条性质，尤其是性质3；
（2）能正确应用性质对不等式进行变形；小结二 当不等式两边都乘以（或除以）同 一个数时，一定要看清是正数还是负数；对于未给定范围的字母，应分情况讨论。注意事项这节课，你有什么收获，能与我们一起分享吗？ 精选作业作业本(2)谢谢大家再见！拓展提高1、若3-2a <3-2b,比较a与b的大小，并说明理由2、若x > y,比较２－３x与２－３y的大小，并说明理由