不等式的基本性质[上学期]

课件21张PPT。 只要代数同几何分道扬镳，他们的进展都会变的缓慢；但若这两门学科结为伴侣，互相促进得力量无人能敌。

——拉格朗日等式的性质1:
　　等式的两边同时加上或减去同一个数
（或式子），等式仍然成立． 等式的性质2：
　等式的两边同时乘以或除以同一个不为
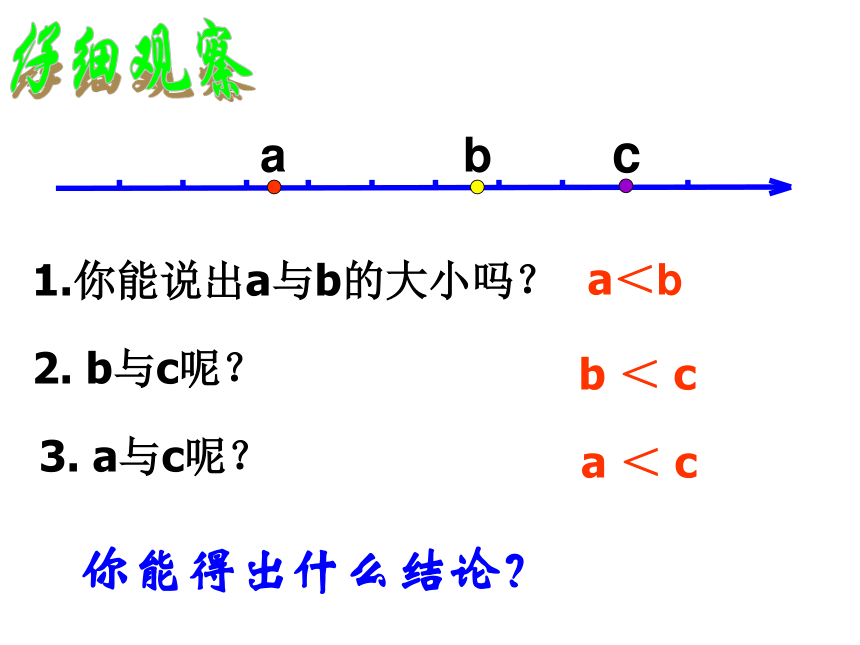
0的数（或式子）， 等式仍然成立．5.2 不等式的基本性质1.你能说出a与b的大小吗？2. b与c呢？3. a与c呢？a＜bb ＜ ca ＜ c你能得出什么结论？仔细观察abc不等式的基本性质1：若a＜b，b＜c，则a＜c。不等式的传递性:1.如果p＞q，q ＞ t，那么p___t.＞2.若a＜b，b＜2c-1，则a____2c-1＜a-cb-ca+cb+c不访设c>0，a＞b，则ab可见，a+c>b+c可见，a-c>b-c-3+2＿＿5+2,-3＿＿5,若a＞b,那么a+c＿＿b+c, a-c＿＿b-c.对于上面数的比较,你发现了什么?＜＜＜＞＞＞＞＞比较大小-3-2＿＿5-2若a＜b,那么a+c＿＿b+c, a-c＿＿b-c.＜＜不等式的基本性质2:如果a＞b,那么a+c＞b+c,a-c＞b-c.
如果a＜b,那么a+c＜b+c,a-c＜b-c. 不等式的两边都加上(或减去)同一个数, 不等号方向不变，所得到的不等式仍成立.学以置用1.选择适当的不等号填空：(1)若a>b,则a+2____b+2;(2)若a<-b,则a+b____0;(3)若-a>-b,则2-a____2-b;＞＜＞＜＜≥≥（不等式的基本性质2）（不等式的基本性质2）从上面的变化,你发现了什么?比较大小6＞26×(-5)____2×(-5)6×5____2×5＞＜＜＞不等式的基本性质3:(1)不等式的两边都乘(或都除以)同一个正数,不等号方向不变，所得到的不等式仍成立;(2)不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得的不等式成立.速记小窍门性质三，不难辨，
乘除正数号不变，
负数是个司令员，
符号见它把头转．及时巩固2.填空：（1）若2x＞ -6 ,两边同除以 2，得 ;
　　(依据：　　　　　　　　　　) （3）若-a ＜ b ,则 a ___ -b；
　　 (依据：　　　　　　　　　　) x ＞-3-2m ＜-3＞不等式的基本性质３不等式的基本性质３不等式的基本性质３不等式的基本性质：性质3：不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立；
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.性质1：若a＜b，b＜c，则a＜c。性质2：不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.（不等号方向不变）（不等号方向不变）（不等号方向改变）（传递性）（6）a＞0，且（1-b）a＜0，则 b____1。3.按下列条件，写出仍成立的不等式。沙场秋点兵27m＞28n3＞1＞1.若a=0，比较a与2a的大小.2.若a＞0，比较a与2a的大小.3.若a＜0，比较a与2a的大小.
4.若a是整数,比较a与2a的大小.变式与思考：a=2aa＜2aa＞2a 一个人一天可以搬运面积为3m2的泥地，要搬完一块面积为100m2的泥地，问至少需要有多少人一天搬完？生活中的应用中考中的应用1.已知 a＜b，那么下列各式中正确的是(?)A. a< – bB. a – 3>b – 8C. a2 < b2D. –3a ＞ – 3bDC(上海市中考题)1.已知 a>b，且c<0那么下面的不等式中
① a+c > b+c　　 ② ac > bc
③ – 　> – 　　　　④ ac2 < bc2.
成立的个数是(?)
A. 1个 B. 2个 C. 3个 D. 4个竞赛中的应用B(第七届“希望杯”试题)竞赛中的应用 2.如果均为有理数a、b,且b＜0，则 a ,a – b，a+b的大小关系是 (?)A. a