一元一次不等式1[上学期]

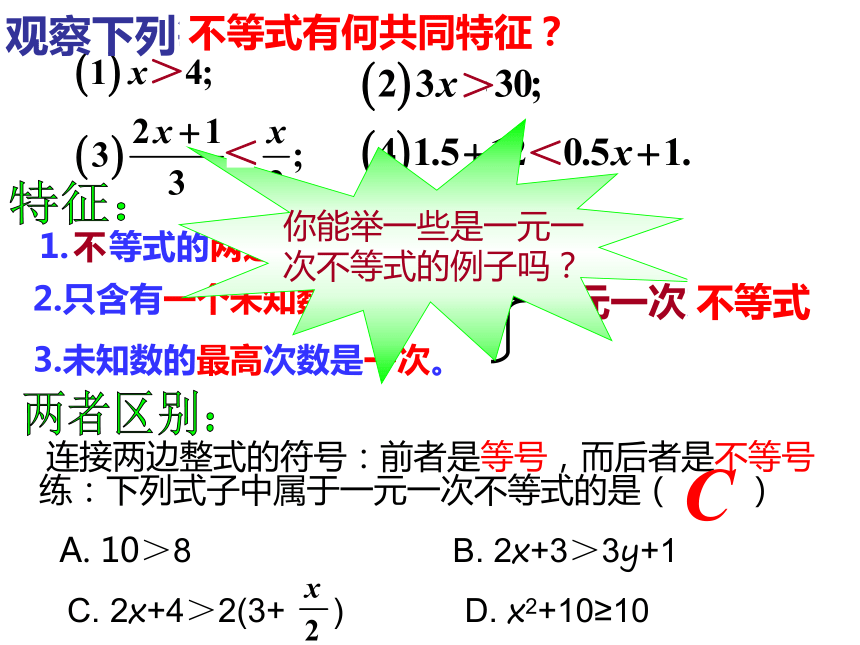
课件10张PPT。5.3一元一次不等式（一）观察下列等式有何共同特征？1. 等式的两边都是整式。2.只含有一个未知数。3.未知数的最高次数是一次。一元一次方程特征：两者区别：连接两边整式的符号：前者是等号，而后者是不等号不等式不不等式有何共同特征？练：下列式子中属于一元一次不等式的是（ ）
A. 10＞8 B. 2x+3＞3y+1
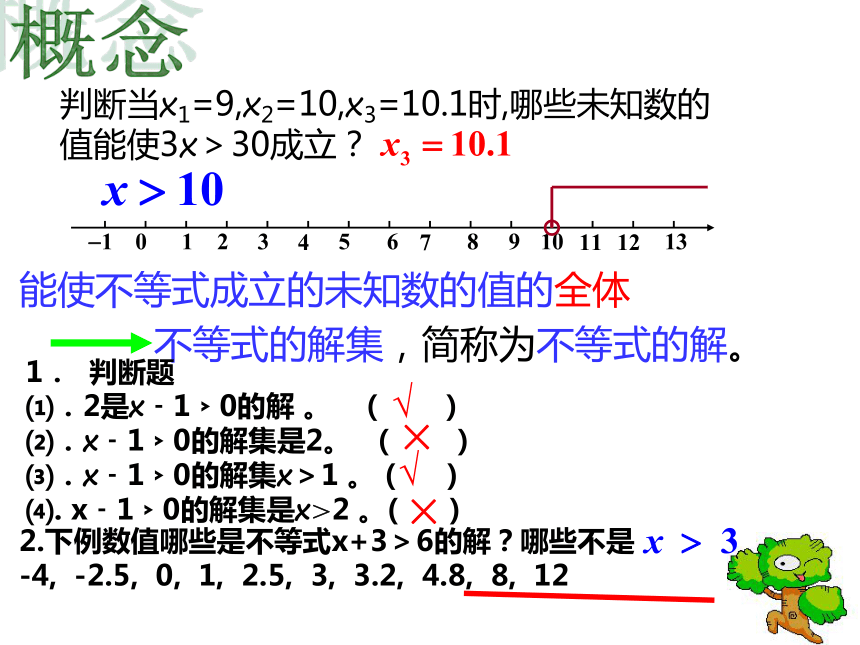
C. 2x+4＞2(3+ ) D. x2+10≥10判断当x1=9,x2=10,x3=10.1时,哪些未知数的值能使3x＞30成立？能使不等式成立的未知数的值的全体不等式的解集，简称为不等式的解。1．? 判断题⑴．2是x﹣1﹥0的解 。 （ ）⑵．x﹣1﹥0的解集是2。 （ ）⑶．x﹣1﹥0的解集x＞1 。 ( )⑷. x﹣1﹥0的解集是x＞2 。( ) √√××2.下例数值哪些是不等式x+3＞6的解？哪些不是-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12概念例1解下列不等式，并把解表示在数轴上：解：两边同除以4，得解：两边同除以 得x≤－2注意1.解不等式就是利用不等式的基本性质，把要
求解的不等式变形成：“x＞a”(或“x≥a”),
“x＜a”(或“x≤a”)2.不等式的两边同乘以（或除以）同一个负数，不等号要改变方向。例2解不等式7x－2≤9x+3，把解表示在数轴上，并求出不等式的负整数解。解 先在不等式的两边同时减去9x，得
7x－9x－2≤3
再在不等式的两边同时加上2，得
7x－9x≤3+2，合并同类项，得
－2x≤5
两边同除以－2，得x≥
由图可得不等式的负整数解是x= -1
和x= -2例2解不等式7x－2≤9x+3，把解表示在数轴上，并求出不等式的负整数解。7x－2≤9x+37x－9x≤3＋2把不等式中的任何一项的符号改变后，从不等号的一边移到另一边，所得到的不等式仍成立。移项法则注意移项时项的符号要改变，不等号的方向不变。课内练习1.下列不等式的解法正确吗？如果不正确，请改正：
（1）－2x＜－4.
解：两边同除以－2，得x＜－2;不正确。应改为x＞2.(2) x+1＞2x－3.
解：移项，得 4＞x,即 x＞4.不正确。应改为x＜4.课内练习2.解下列不等式，并把解表示在数轴上：
(1)1－x＞2; (2)5x－4＞4－3x;
(3) ≤1; (4)6x－1＞9x－4.3.解不等式 ，把解表示在数轴上，
并求出适合不等式的正整数解。作业：
1.课后作业题
2.作业本
再见提高题1.不等式（a+1）x＞ （a+1）的解集是x＜1，则a的取值范围是（ ）
A. a＜0 B. a＜1
C. a＜－1 D. a＞－12.三个连续正奇数之和小于16，则这三个正奇数是_____________________.3.已知y=3x－2，要使y＜x，则x的取值范围是______________。1，3，5或3，5，7