5.4一元一次不等式组(第一课时).[上学期]
文档属性
| 名称 | 5.4一元一次不等式组(第一课时).[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 366.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-03 18:00:00 | ||
图片预览



文档简介
课件14张PPT。小结: (1)一元一次不等式组的概念
(2)一元一次不等式组的解的概念
(3)解一元一次不等式组的步骤和 解的四种情况.作业: (1)作业本5.1(1)
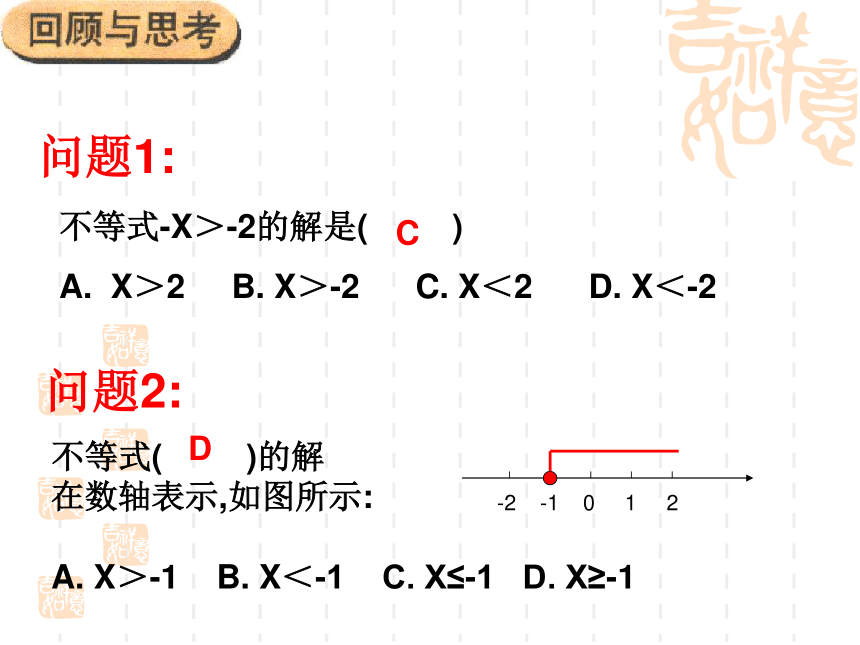
(2)课本中作业题(1)不等式-X>-2的解是( )
A. X>2 B. X>-2 C. X<2 D. X<-2 C问题1:问题2:D作业本(2) P24甲、乙两地的距离在200千米至240千米之间(包括200和240)。一辆汽车的速度为每小时80千米。这辆汽车从甲地出发,需行驶多少时间才能到达乙地?分析:设行驶的时间为x小时,则行驶了多少路程?与200、240又有怎样的不等关系? 80X≥20080X≤240问题3:某单位从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔每桶的单价如图所示,设购买圆珠笔X桶,你能列出几个不等式?问题4:44.9X+34.9(15-X) <580
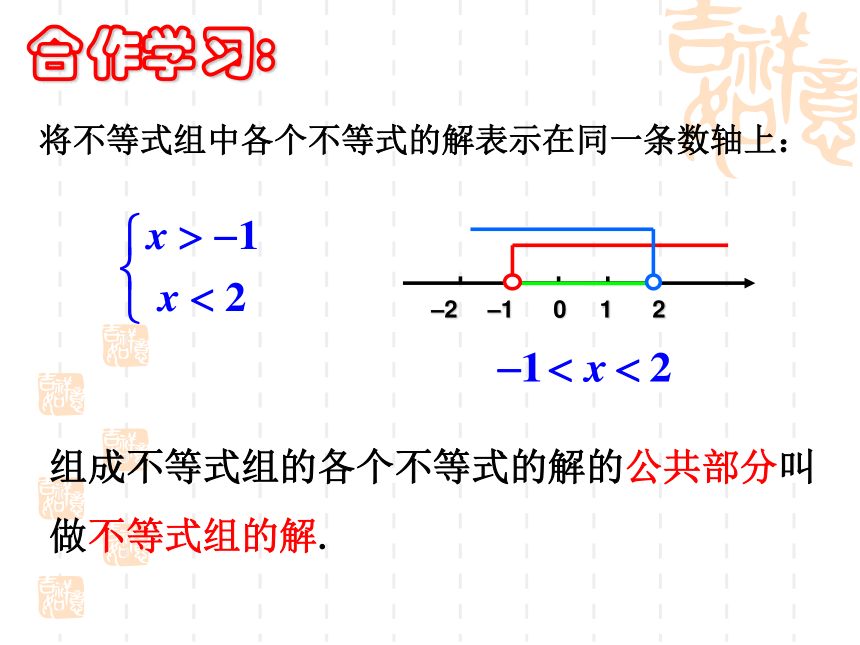
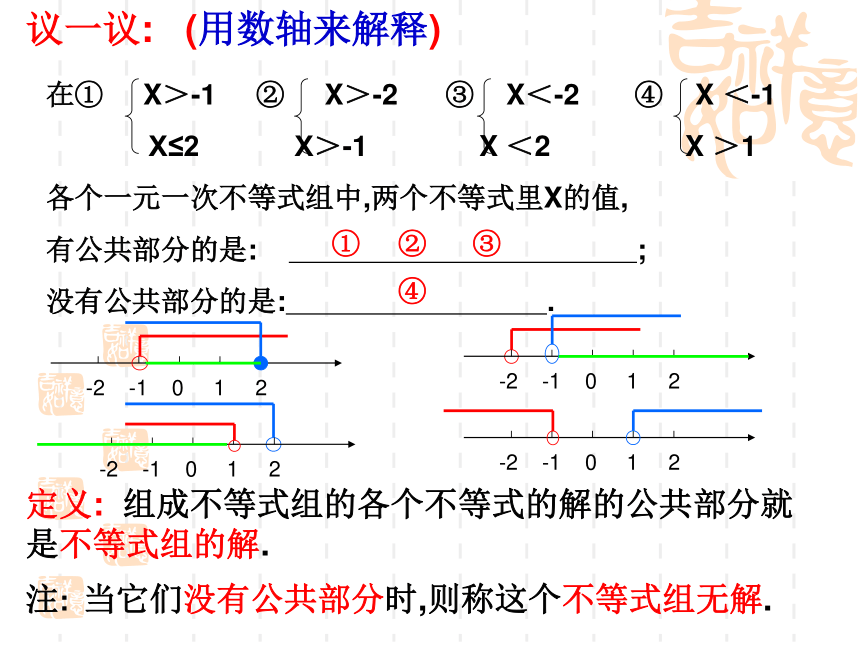
44.9X+34.9(15-X) >570定义: 一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.实际生活还有这样的例子吗?组成不等式组的各个不等式的解的公共部分叫做不等式组的解.合作学习:将不等式组中各个不等式的解表示在同一条数轴上:议一议: (用数轴来解释)在① X>-1 ② X>-2 ③ X<-2 ④ X <-1
X≤2 X>-1 X <2 X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
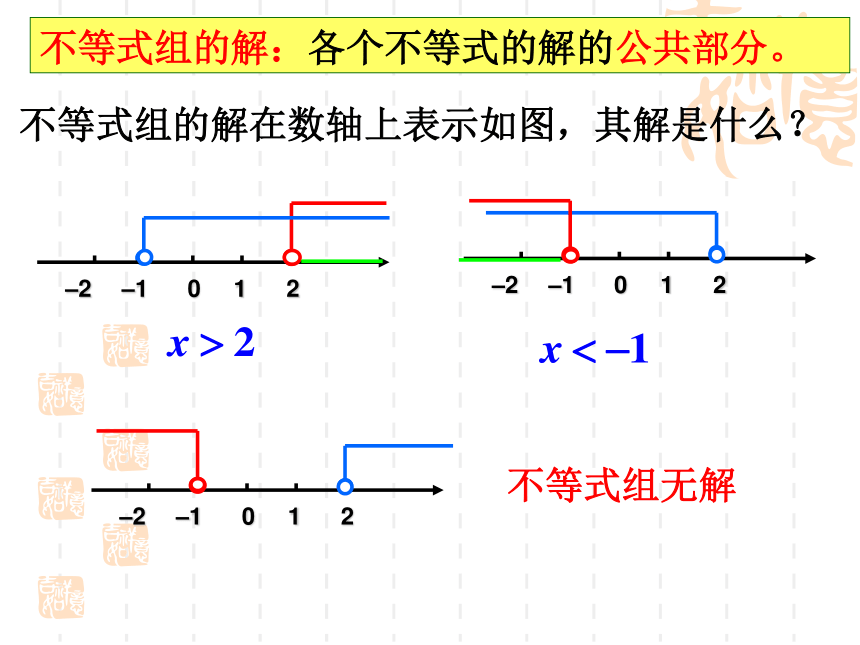
没有公共部分的是: .②④定义: 组成不等式组的各个不等式的解的公共部分就是不等式组的解. ① ③ 注: 当它们没有公共部分时,则称这个不等式组无解.不等式组的解在数轴上表示如图,其解是什么?不等式组无解不等式组的解:各个不等式的解的公共部分。分析: 根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.解一元一次不等式组的步骤:(1)依次求解每个不等式(2)将每个不等式的解表示在同一条数轴上(3)利用数轴找出公共部分(原不等式组的解)例 题 解 析解一元一次不等式组的步骤:(1)依次求解每个不等式(2)将每个不等式的解表示在同一条数轴上(3)利用数轴找出公共部分(原不等式组的解)练一练:1.解下列各一元一次不等式组 2.求出P115节前图中,圆珠笔和墨水笔的桶数.解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?探索研究若m<n,你能说出下列四种情况下,不等式组的解吗?用数轴试一试.(请你与同伴交流)m<x<n ; x>n ; x<m ; 无解大小小大, 大大,取大 小小,取小 小小大大,
取两数之间 无解注: 以上规律建立在最简不等式组的基础上思考题:1.解不等式组: 2-x<x≤6-2xA解为 1<x≤2你有什么收获?
(2)一元一次不等式组的解的概念
(3)解一元一次不等式组的步骤和 解的四种情况.作业: (1)作业本5.1(1)
(2)课本中作业题(1)不等式-X>-2的解是( )
A. X>2 B. X>-2 C. X<2 D. X<-2 C问题1:问题2:D作业本(2) P24甲、乙两地的距离在200千米至240千米之间(包括200和240)。一辆汽车的速度为每小时80千米。这辆汽车从甲地出发,需行驶多少时间才能到达乙地?分析:设行驶的时间为x小时,则行驶了多少路程?与200、240又有怎样的不等关系? 80X≥20080X≤240问题3:某单位从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔每桶的单价如图所示,设购买圆珠笔X桶,你能列出几个不等式?问题4:44.9X+34.9(15-X) <580
44.9X+34.9(15-X) >570定义: 一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.实际生活还有这样的例子吗?组成不等式组的各个不等式的解的公共部分叫做不等式组的解.合作学习:将不等式组中各个不等式的解表示在同一条数轴上:议一议: (用数轴来解释)在① X>-1 ② X>-2 ③ X<-2 ④ X <-1
X≤2 X>-1 X <2 X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
没有公共部分的是: .②④定义: 组成不等式组的各个不等式的解的公共部分就是不等式组的解. ① ③ 注: 当它们没有公共部分时,则称这个不等式组无解.不等式组的解在数轴上表示如图,其解是什么?不等式组无解不等式组的解:各个不等式的解的公共部分。分析: 根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.解一元一次不等式组的步骤:(1)依次求解每个不等式(2)将每个不等式的解表示在同一条数轴上(3)利用数轴找出公共部分(原不等式组的解)例 题 解 析解一元一次不等式组的步骤:(1)依次求解每个不等式(2)将每个不等式的解表示在同一条数轴上(3)利用数轴找出公共部分(原不等式组的解)练一练:1.解下列各一元一次不等式组 2.求出P115节前图中,圆珠笔和墨水笔的桶数.解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?探索研究若m<n,你能说出下列四种情况下,不等式组的解吗?用数轴试一试.(请你与同伴交流)m<x<n ; x>n ; x<m ; 无解大小小大, 大大,取大 小小,取小 小小大大,
取两数之间 无解注: 以上规律建立在最简不等式组的基础上思考题:1.解不等式组: 2-x<x≤6-2xA解为 1<x≤2你有什么收获?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
