5.3 一元一次不等式(2)[上学期]
图片预览





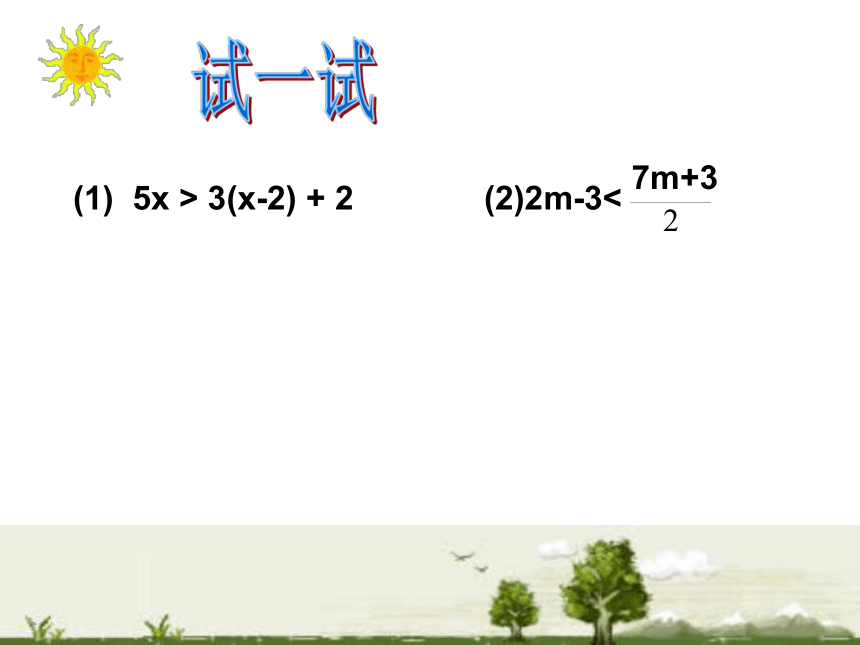
文档简介
课件12张PPT。5.3 一元一次不等式(2)不等式的概念在数轴上表示X<a?在数轴上表示X≥a?在数轴上表示b<X<a(b<a)?回顾性质1:
若a<b,b<c,则a<c。
性质2:
如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b,那么a+c<b+c,a-c<b-c.
性质3:
如果a>b,且c>0,那么ac>bc,a÷c>b÷c.
如果a>b,且c<0,那么ac<bc,a÷c<b÷c.回顾不等式的基本性质先解下列一元一次方程,再思考需要哪几个步骤?3x - (2 - x) = 5x如果系数为分数呢?解一元一次方程的步骤:在方程两边都乘以各分母的最小公倍数等式
性质2不要漏乘不含分母的项一般先去小括号,再去中括号,最后去大括号分配律 去括号法则不要漏乘括号中的每一项把含有未知数的项移到 方 程 一边,其它项都移到 方 程 另一边,注意移项要变号移项法则 1)移动的项一定要变号,
不移的项不变号 2)注意项较多时不要漏项把方程变为ax=b
(a≠0 ) 的最简形式合并同类项法则2)字母和字母的指数不变将方程两边都除以未知数系数a,得解x=b/a等式性质2解的分子,分母位置不要颠倒1)把系数相加一元一次不等式不等式不等式基
本性质3不等式变号问题.不等式不等式不等式基
本性质2 得 ax>b或
ax不等式基
本性质3不等式变号问题.
试一试(1) 5x > 3(x-2) + 2 (2)2m-3<例题讲解例3解不等式 3(1 - x) > 2(1 - 2x) 解:去括号,得 3 - 3x > 2 - 4x 移项,得 - 3x + 4x > 2 - 3合并同类项,得 x > - 1例4解不等式≤并把解在数轴上表示出来.练一练P106 课内练习
1. 3x – 5 < 2(2 + 3x)挑战自我2. 3(5 – x) > 2(x - 2) - 43. ≥4.<通过这节课的学习,你学到了什么?小结谢谢
若a<b,b<c,则a<c。
性质2:
如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b,那么a+c<b+c,a-c<b-c.
性质3:
如果a>b,且c>0,那么ac>bc,a÷c>b÷c.
如果a>b,且c<0,那么ac<bc,a÷c<b÷c.回顾不等式的基本性质先解下列一元一次方程,再思考需要哪几个步骤?3x - (2 - x) = 5x如果系数为分数呢?解一元一次方程的步骤:在方程两边都乘以各分母的最小公倍数等式
性质2不要漏乘不含分母的项一般先去小括号,再去中括号,最后去大括号分配律 去括号法则不要漏乘括号中的每一项把含有未知数的项移到 方 程 一边,其它项都移到 方 程 另一边,注意移项要变号移项法则 1)移动的项一定要变号,
不移的项不变号 2)注意项较多时不要漏项把方程变为ax=b
(a≠0 ) 的最简形式合并同类项法则2)字母和字母的指数不变将方程两边都除以未知数系数a,得解x=b/a等式性质2解的分子,分母位置不要颠倒1)把系数相加一元一次不等式不等式不等式基
本性质3不等式变号问题.不等式不等式不等式基
本性质2 得 ax>b或
ax
本性质3不等式变号问题.
试一试(1) 5x > 3(x-2) + 2 (2)2m-3<例题讲解例3解不等式 3(1 - x) > 2(1 - 2x) 解:去括号,得 3 - 3x > 2 - 4x 移项,得 - 3x + 4x > 2 - 3合并同类项,得 x > - 1例4解不等式≤并把解在数轴上表示出来.练一练P106 课内练习
1. 3x – 5 < 2(2 + 3x)挑战自我2. 3(5 – x) > 2(x - 2) - 43. ≥4.<通过这节课的学习,你学到了什么?小结谢谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
