第4章《相似三角形》单元提升卷(含解析)
文档属性
| 名称 | 第4章《相似三角形》单元提升卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 616.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2022-2023相似三角形提升卷(含解析)
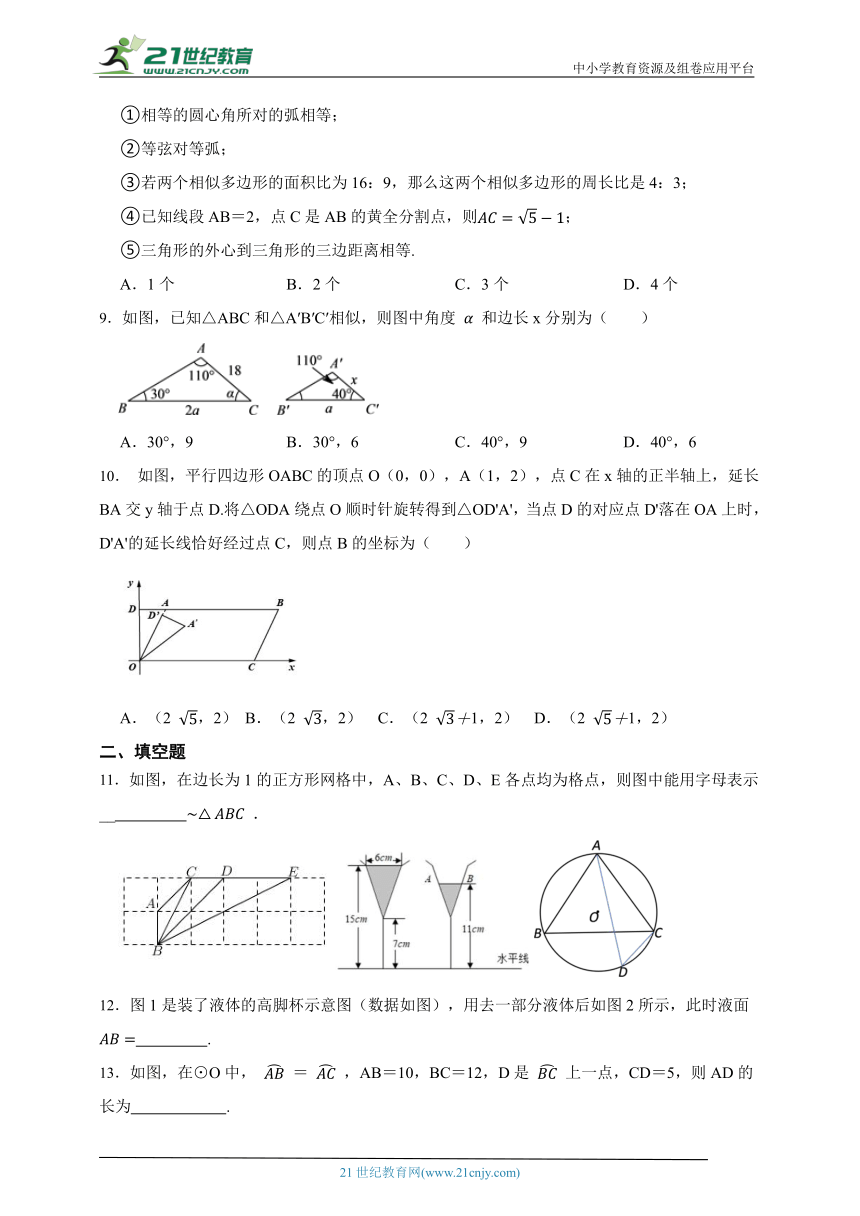
一、单选题
1.若,则的值为( )
A. B. C. D.
2.下列结论中,不正确的是( )
A.若,则 B.若,则
C.若(b﹣d≠0),则 D.若,则a=3,b=4
3.下列格点三角形中,与右侧已知格点相似的是( )
A. B.C. D.
4.若矩形ABCD∽矩形EFGH,相似比为2∶3,已知AB=3 cm,BC=5 cm,则矩形EFGH的周长是( )
A.16 cm B.12 cm C.24 cm D.36 cm
5.如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )
A. B.
C. D.
6.已知的三边长是,,2,则与相似的三角形的三边长可能是( )
A.1,, B.1,, C.1,, D.1,,
7.如图,,直线与这三条平行线分别交于点A、B、C和点D、E、F,若,则DE的长度是( )
A. B. C.6 D.10
8.下列语句中,正确的有( )
①相等的圆心角所对的弧相等;
②等弦对等弧;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3;
④已知线段AB=2,点C是AB的黄全分割点,则;
⑤三角形的外心到三角形的三边距离相等.
A.1个 B.2个 C.3个 D.4个
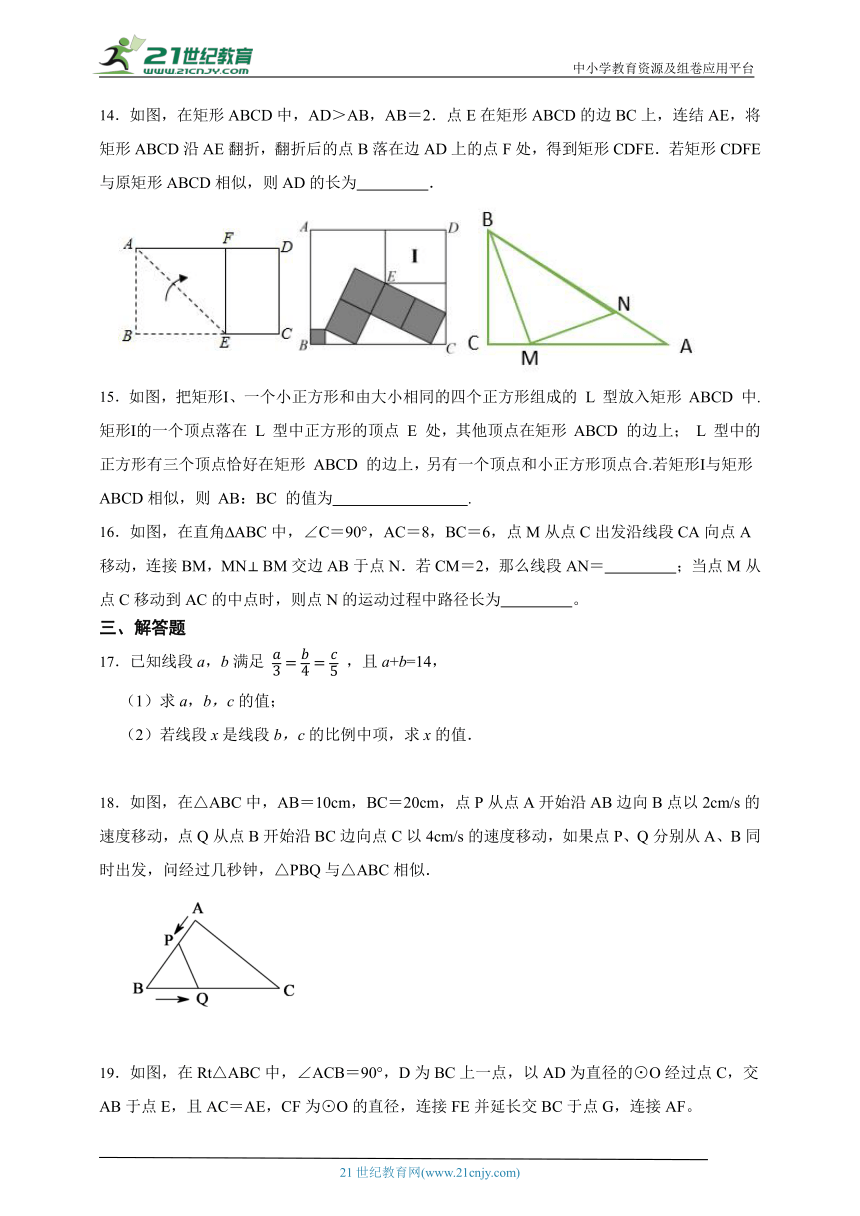
9.如图,已知△ABC和△A′B′C′相似,则图中角度 和边长x分别为( )
A.30°,9 B.30°,6 C.40°,9 D.40°,6
10. 如图,平行四边形OABC的顶点O(0,0),A(1,2),点C在x轴的正半轴上,延长BA交y轴于点D.将△ODA绕点O顺时针旋转得到△OD'A',当点D的对应点D'落在OA上时,D'A'的延长线恰好经过点C,则点B的坐标为( )
A.(2
,2) B.(2
,2) C.(2
1,2) D.(2
1,2)
二、填空题
11.如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示__ .
12.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 .
13.如图,在⊙O中, = ,AB=10,BC=12,D是 上一点,CD=5,则AD的长为 .
14.如图,在矩形ABCD中,AD>AB,AB=2.点E在矩形ABCD的边BC上,连结AE,将矩形ABCD沿AE翻折,翻折后的点B落在边AD上的点F处,得到矩形CDFE.若矩形CDFE与原矩形ABCD相似,则AD的长为 .
15.如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处,其他顶点在矩形 ABCD 的边上; L 型中的正方形有三个顶点恰好在矩形
ABCD 的边上,另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形
ABCD相似,则 AB:BC 的值为 .
16.如图,在直角 ABC中,∠C=90°,AC=8,BC=6,点M从点C出发沿线段CA向点A移动,连接BM,MN BM交边AB于点N.若CM=2,那么线段AN= ;当点M从点C移动到AC的中点时,则点N的运动过程中路径长为 。
三、解答题
17.已知线段a,b满足 ,且a+b=14,
(1)求a,b,c的值;
(2)若线段x是线段b,c的比例中项,求x的值.
18.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.
19.如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的⊙O经过点C,交AB于点E,且AC=AE,CF为⊙O的直径,连接FE并延长交BC于点G,连接AF。
(1)求证:四边形ADGF是平行四边形;
(2)若AF:BC=3:8,BE=4,求⊙O的直径。
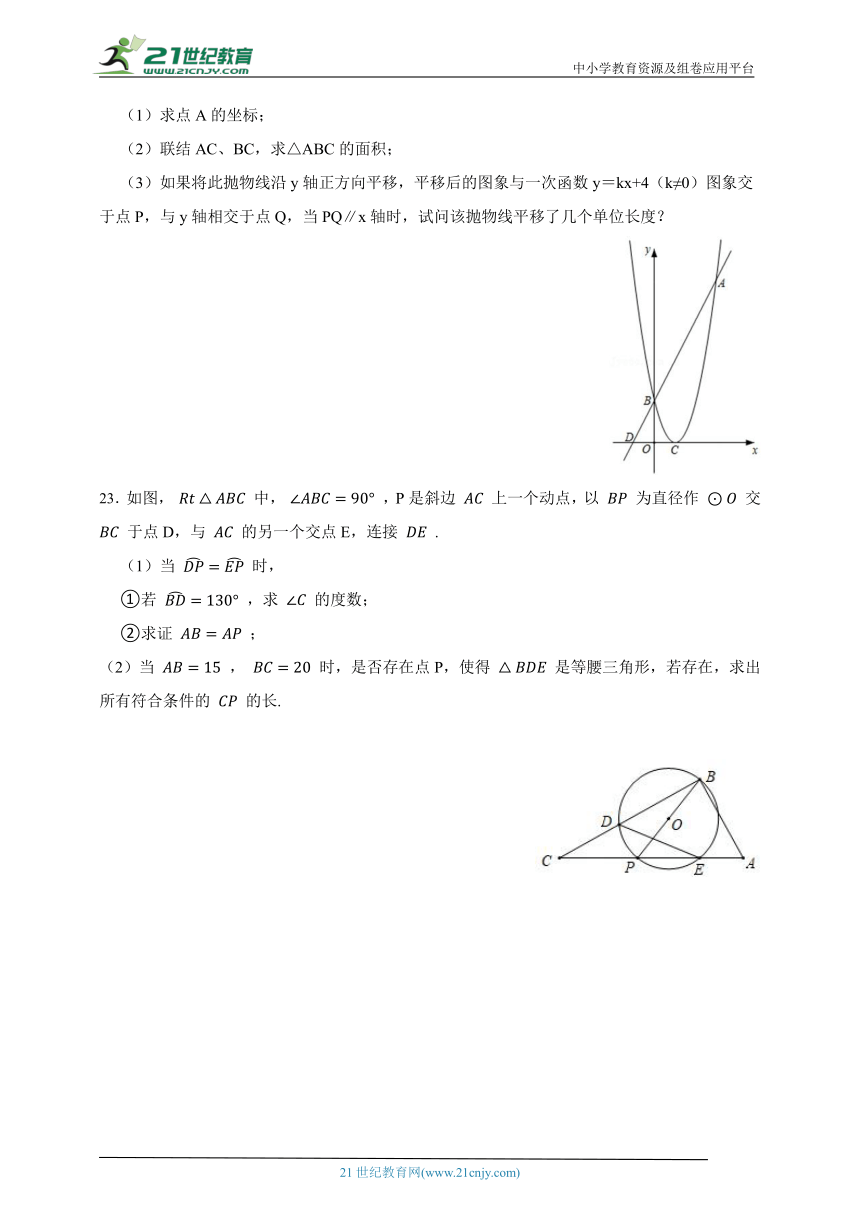
20.在 中, , 垂直平分 ,分别交 于点 .
(1)求证: ;
(2)求证: .
21.在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)用含t的代数式表示:线段PO= cm;OQ= cm.
(2)当t为何值时△POQ的面积为6cm2?
(3)当△POQ与△AOB相似时,求出t的值.
22.如图,已知在平面直角坐标系xOy中,抛物线y=(x﹣2)2的顶点为C,与y轴正半轴交于点B,一次函数y=kx+4(k≠0)图象与抛物线交于点A、点B,与x轴负半轴交于点D,若AB=3BD.
(1)求点A的坐标;
(2)联结AC、BC,求△ABC的面积;
(3)如果将此抛物线沿y轴正方向平移,平移后的图象与一次函数y=kx+4(k≠0)图象交于点P,与y轴相交于点Q,当PQ∥x轴时,试问该抛物线平移了几个单位长度?
23.如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .
(1)当 时,
①若 ,求 的度数;
②求证 ;
(2)当 , 时,是否存在点P,使得 是等腰三角形,若存在,求出所有符合条件的 的长.
24.如图
如图1,把两个相似比为 的矩形ABCD与矩形CEFG拼成如图所示的图案.
(1)(一)问题发现:
请探究AC与CF的位置关系并证明.
(2)求 的值.
(3)(二)拓展应用:
如图2,在四边形ABCF中,已知∠ABC=90°,AB=3,BC=4,CF=10,AF=5 .
连接BF,求BF的长.
答案解析部分
1.【答案】D
【解析】【解答】解:∵,
∴x=y,
∴,
故答案为:D.
【分析】由已知条件可得x=y,然后代入中化简即可.
2.【答案】D
【解析】【解答】解:A、若,则,而,,不合题意;
B、若,则6(a﹣b)=b,故6a=7b,则,不合题意;
C、若(b﹣d≠0),则,则,不合题意;
D、若,设,当k=1时,有a=3,b=4,当k≠1, a,b的值不是3与4,符合题意.
故答案为:D.
【分析】根据比例的性质逐项判断即可。
3.【答案】A
【解析】【解答】解:的三边长分别为:,
,,
∵,
∴为直角三角形,B,C选项不符合题意,排除;
A选项中三边长度分别为:2,4,,
∴,
A选项符合题意,
D选项中三边长度分别为:,,,
∴,
故答案为:A.
【分析】根据相似三角形的判定方法逐项判断即可。
4.【答案】C
【解析】【解答】∵AB=3cm,BC=5cm,
∴矩形ABCD的周长=2×(3+5)=16cm,
∵矩形ABCD∽矩形EFGH,相似比为2:3,
∴矩形ABCD与矩形EFGH的周长比2:3,
∴矩形EFGH的周长为24cm,
故答案为:C.
【分析】先求出矩形ABCD的周长为16cm,再求出矩形ABCD与矩形EFGH的周长比2:3,最后计算求解即可。
5.【答案】C
【解析】【解答】解:∵DE∥BC,
∴ ,
∴ ,故A选项错误,不符合题意;
,故B选项错误,不符合题意;
,故C选项正确,符合题意;
∴ ,故D选项错误,不符合题意.
故答案为:C.
【分析】易证△ADE∽△ABC,然后根据相似三角形的对应边成比例、相似三角形的周长之比等于相似比,面积之比等于相似比的平方进行判断.
6.【答案】A
【解析】【解答】解:∵△ABC三边长是,,2,
∴△ABC三边长的比为:2:=1::,
∴△ABC相似的三角形三边长可能是1::,
故答案为:A.
【分析】根据相似三角形对应边的比相等进行解答即可.
7.【答案】C
【解析】【解答】解:由平行线分线段成比例可知
∴
解得
故答案为:C.
【分析】根据平行线分线段成比例的性质可得,再将数据代入计算即可。
8.【答案】A
【解析】【解答】解:①在同圆或等圆中,相等的圆心角所对的弧相等,原说法错误,故不符合题意;
②在同圆或等圆中,等弦所对的优弧相等,等弦所对的劣弧相等,原说法错误,故不符合题意;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3,原说法正确,故符合题意;
④已知线段AB=2,点C是AB的黄全分割点,
则或,原说法错误,故不符合题意;
⑤三角形的外心到三角形的三个顶点距离相等,原说法错误,故不符合题意.
故答案为:A.
【分析】根据弧、弦、圆心角的关系,相似多边形的性质、黄全分割点、三角形的外心的性质分别进行判断即可.
9.【答案】C
【解析】【解答】解:由题意:△ABC∽△A′B′C′,
∴∠ =∠ =40°,
,即 ,
∴解得 ,
经检验 符合意义,是原方程的解.
故答案为:C.
【分析】根据相似三角形对应角相等可得∠α的度数,根据相似三角形对应边成比例可得x的值.
10.【答案】D
【解析】【解答】解:如图,连接A'C,AD⊥y轴,△ODA绕点O顺时针旋转得到△OD'A',
∴,
,
,
,
∵,
,
,
,
,
,
,
,
∴,
∴,
∴点B的坐标为:
,
故答案为:D.
【分析】连接A'C,AD⊥y轴,△ODA绕点O顺时针旋转得到△OD'A',由同角的余角相等可得∠DOA=∠D'CO,根据有两个角对应相等的两个三角形相似可得△ADO∽△OD'C,则可得比例式
,根据比例式求出CO,由平行四边形的性质得OC=AB,由线段的构成DB=AD+AB求得DB的值,则点B的坐标可求解.
11.【答案】△DEB
【解析】【解答】解:根据题意可得: , , ,
∴ ,
故答案为:△DEB.
【分析】利用相似三角形的判定方法判断求解即可。
12.【答案】3
【解析】【解答】解:依题意,两高脚杯中的液体部分两三角形相似,则
解得 .
故答案为:3.
【分析】依题意可知:两高脚杯中的液体部分两三角形相似,然后根据对应边成比例可得AB.
13.【答案】3+2
【解析】【解答】解:过A作AE⊥BC于E,过C作CF⊥AD于F,则∠AEB=∠CFD=90°,
∵ = , AB=10,
∴∠ACB=∠B=∠D,AB=AC=10,
∵AE⊥BC,BC=12,
∴BE=CE=6,
∴ ,
∵∠B=∠D,∠AEB=∠CFD=90°,
∴△ABE∽△CDF,
∴ ,
∵AB=10,CD=5,BE=6,AE=8,
∴ ,
解得:DF=3,CF=4,
在Rt△AFC中,∠AFC=90°,AC=10,CF=4,
则 ,
∴AD=DF+AF=3+2 .
故答案为:3+2 .
【分析】过A作AE⊥BC于E,过C作CF⊥AD于F,则∠AEB=∠CFD=90°,根据同弧或等弧所对的圆周角相等可得∠ACB=∠B=∠D,根据等弧所对的弦相等得AB=AC=10,由等腰三角形的三线合一得BE=CE=6, 利用勾股定理可得AE,证明△ABE∽△CDF,根据相似三角形的性质可得DF、CF,利用勾股定理求出AF,然后根据AD=DF+AF进行计算.
14.【答案】
【解析】【解答】∵矩形CDFE∽矩形ADCB,
∴ = ,即 = ,
整理得,AD2﹣2AD﹣4=0,
解得,AD1=1﹣ (舍去),AD2= ,
故答案为: .
【分析】根据矩形CDFE∽矩形ADCB,可得 = ,再将数据代入计算可得AD2﹣2AD﹣4=0,最后解一元二次方程即可。
15.【答案】 或
【解析】【解答】解:设大小相同的四个正方形的边长为a,DF=x,即GH=IJ=KJ=a,IH=EG=2a,
在Rt△IJH中,JH=
a,
∵四边形ABCD和四边形MEFD是矩形,四边形NBLK是矩形,
4个完全相同的小正方形组成的L型模板如图放置,
∴∠B=∠C=∠KLJ=∠EFG=∠JIH=90°,
∴∠LKJ+∠LJK=∠IJH+∠IHJ=∠GHC+∠HGC=∠EGF+∠GEF=90°,
∠KJL+∠IJH=∠IHJ+∠GHC=∠EGF+∠HGC=90°,
∴∠KJL=∠IHJ=∠HGC=∠GEF,
∴△KJL≌△HGC,△JHI∽△HGC∽△GEF,
∴BL=KL=HC,LJ=GC,
,
,
即
,
,
∴FG=
,EF=
,BL=KL=HC=
,LJ=GC=
,
∴CD=DF+FG+GC=x+
=
,
BC=BL+LJ+JH+HC=
+
=
,
当矩形MEFD∽矩形 ABCD时,
,即
,
解得:x=
,
AB:BC 的值为
;
当矩形MDFE∽矩形 ABCD时,
,即
,
解得:x=
(负值已舍),
AB:BC 的值为
;
故答案为:
或
.
【分析】设大小相同的四个正方形的边长为a,DF=x,即GH=IJ=KJ=a,IH=EG=2a,由勾股定理得JH= a,根据矩形的性质得∠B=∠C=∠KLJ=∠EFG=∠JIH=90°,由同角的余角相等得∠KJL=∠IHJ=∠HGC=∠GEF,证△KJL≌△HGC,△JHI∽△HGC∽△GEF,根据全等三角形的性质可得BL=KL=HC,LJ=GC,根据相似三角形的性质可得FG、EF,进而得到BL、LJ、CD、BC,根据相似矩形的对应边成比例可得x的值,进而可得AB:BC的值.
16.【答案】;
【解析】【解答】解:(1)如图,作ND⊥AC
易得AB=10
易得
∴
设ND=x,则MD=3x
则AD=AC-CM-MD=6-3x
易得
∴
∴
∴AN=
(2)同(1)理,得出AN=
故答案为:;.
【分析】由三垂直,得出,得出,设出未知数,由平行,得出,得出方程,从而得出结果。
17.【答案】(1)解:设 ,则a=3k,b=4k,c=5k,
∵a+b=14,
∴3k+4k=7k=14,
解得k=2,
∴a=6,b=8,c=10
(2)解:∵b=8,c=10,x是b,c的比例中项,
∴x2=8×10=80,
解得
【解析】【分析】(1)利用已知条件a=3k,b=4k,c=5k,根据a+b=14,可求出k的值,然后求出a,b,c的值.
(2)利用x是b,c的比例中项, 可得到x2=bc,代入可得到关于x的方程,解方程求出x的值.
18.【答案】解:设经过t秒后,△PBQ与△ABC相似,则有,,,
当时,,
即,
解得秒;
当时,,
即,
解得秒.
∴经过2.5秒或1秒时,△PBQ与△ABC相似.
【解析】【分析】分两种情况:①当时,,②当时,,再将数据代入求解即可。
19.【答案】(1)证明:连接CE.
∵AC=AE,
∴ ,
∴AD⊥CE,
∵CF是直径,
∴∠CEF=90°,
∴FG⊥CE,
∴AD∥FG,
∵CF,AD是直径,
∴∠ACD=∠CAF=90°,
∴∠CAF+∠ACD=180°,
∴AF∥BC,
∴四边形ADGF是平行四边形.
(2)解:∵∠AOF=∠COD,
∴ ,
∴AF=CD,
∵四边形ADGF是平行四边形,
∴AF=DG,
∵AF:BC=3:8,
∴BG:DG=2:3,
∵EG∥AD,
∴ ,
∵BE=4,
∴AE=AC=6,
∴AB=10,BC= =8,
∵CD=DG,BG:DG=2:3,
∴CD=GD=3,BG=2,
∴AD= =3 ,
∴⊙O的直径为3
【解析】【分析】(1)根据垂径定理得出AD⊥CE,然后根据圆周角定理求出FG⊥CE,可得AD∥FG,根据直径所对的圆周角是直角求出∠CAF+∠ACD=180°,可得AF∥BC,从而证出四边形ADGF是平行四边形.
(2) 根据平行四边形的性质和圆心角和弦的关系求出AF=CD=DG,可得BG:DG=2: 3,利用平行线分线段成比例定理求出AE、AC,再利用勾股定理求出BC、CD,即可求出结果.
20.【答案】(1)证明: ,
,
垂直平分 AB ,
,
,
,
,
;
(2)解:证明:由(1)知 ,
,
,
,
,
,
.
【解析】【分析】(1)根据等腰三角形的性质以及内角和定理可得∠ABC=∠C=72°,根据垂直平分线的性质可得AE=BE,根据等腰三角形的性质可得∠ABE=∠A=36°,推出∠BEC=∠C,据此证明;
(2)易证△BEC∽△ABC,然后根据相似三角形的性质证明即可.
21.【答案】(1)2t;(5﹣t)
(2)解:由(1)知,OP=2t cm,OQ=(5-t)cm,
∵△POQ的面积为6cm2,
∴6=×2t×(5-t),
∴t=2或3,
∴当t=2或3时,三角形POQ的面积为6cm2;
(3)解:∵△POQ与△AOB相似,∠POQ=∠AOB=90°,
∴△POQ∽△AOB或△POQ∽△BOA,
∴或,
当,则,
∴t=;
当时,则,
∴t=1,
∴当t=或1时,△POQ与△AOB相似.
【解析】【解答】(1)解:由题意知,OP=2t cm,BQ=t cm,
∴OQ=(5-t)cm,
故答案为:2t,(5-t);
【分析】(1)由题意知,OP=2t cm,BQ=t cm,则OQ=(5-t)cm;
(2)由(1)可得S==6 ,解之可得t;
(3)由题意可知 △POQ与△AOB相似分为两种情况,△POQ∽△AOB和△POQ∽△BOA,可根据相似三角形的性质对应线段成比例求出t的值。
22.【答案】(1)解:作AE⊥x轴与点E,则BO∥AE,
将x=0代入y=(x﹣2)2得y=4,
∴点B坐标为(0.4).
∵AB=3BD,
∴.
∴AE=4BO=16,
将y=16代入y=(x﹣2)2得16=(x﹣2)2,
解得x=6或x=﹣2(舍),
∴点A坐标为(6,16).
(2)作CF∥y轴交AB于点F,
将(6,16)代入y=kx+4得16=6k+4,
解得k=2,
∴y=2x+4,
将x=2代入y=2x+4得y=8,
∴点F坐标为(2,8),
∴FC=8,
∴S△ABC=S△BCF+S△ACF= FC (xC﹣xB)+FC (xA﹣xC)=×8×(2﹣0)+×8×(6﹣2)=24.
(3)设抛物线向上平移m个单位,则点P坐标为(0,4+m),
由题意可得P,Q关于对称轴对称,
∴点Q坐标为(4,4+m),
将(4,4+m)代入y=2x+4得4+m=8+4,
解得m=8,
∴该抛物线平移了8个单位.
【解析】【分析】(1)作AE⊥x轴与点E,先求出点B的坐标为(0,4),再根据平行线分线段成比例定理得出AE=16,再把y=16代入抛物线的解析式求出x的值,即可得出点A的坐标;
(2)作CF∥y轴交AB于点F,利用待定系数法求出直线AB的解析式,再求出点F的坐标,利用 S△ABC=S△BCF+S△ACF列式进行计算,即可得出答案;
(3)设抛物线向上平移m个单位,得出点P坐标为(0,4+m),从而得出点Q坐标为(4,4+m),再把点Q的坐标代入直线AB的解析式,求出m的值,即可得出答案.
23.【答案】(1)解:①如图,连接PD,
∵PB为直径,
∴∠PDB=90°,
∠BPD=65°,
∴∠PBD=90°-∠BPD=25°,
∵ ,
∴,
∴,
∴∠C=∠BPE-∠PBD=65°-25°=40°;
② 证明:∵,
∴∠CBP=∠EBP,
∵∠ABE+∠A=∠C+∠A=90°,
∴∠C=∠ABE,
∴∠ABP=∠ABE+∠EBP,∠APB=∠C+∠CBP,
∴∠ABP=∠APB,
∴AP=AB;
(2)解:存在,
如图,连接PD,
由AB=15,BC= 20,
由勾股定理得: AC= = =25,
∵AB.BC=AC.BE ,
即×15×20=×25×BE,
∴ BE=12,
∵BP是直径,
∴∠PDB =90° ,
∵∠ABC =90° ,
∴PD∥AB ,
∴△DCP∽△BCA ,
∴,
∴,
△BDE是等腰角形,分三种情况:
当BD= BE时,BD=BE=12,
∴CD=BC-BD=20-12=8,
∴ CP=CD=x8=10,
当BD= ED时,可知点D是Rt△CBE斜边的中线,
∴CD=BC=10,
∴CP=CD=×10=,
当DE=BE时,作EH⊥BC, 则H是BD中点,EH//AB, 如图,
AE== =9,
:.CE=AC-AE=25-9=16, CH=BC-BH=20-BH ,
∵EH∥AB,
∴,
即,
解得: BH= ,
∴BD=2BH=,
∴CD= BC-BD=20-=,
∴CP=CD=,
综上所述,△BDE 是等腰三角形,符合条件的CP的长为10或或7.
【解析】【分析】(1)如图,连接PD,
① 根据直径所对的圆周角是直角,结合求得∠BPD的大小,则度数可求,从而求出的度数,最后利用三角形外角的性质求出∠C的度数即可;
② 由弧相等得角相等,再由余角的性质得∠C=∠ABE,于是角的关系即可得出∠ABP=∠APB,从而证出AP=AB;
(2)由勾股定理得AC=25,由面积公式得出AB BC=AC BE,求出BE=12,连接DP,则PD∥AB,得出△DCP∽△BCA,求出CP==,CD,
△BDE是等腰三角形,分三种情况讨论,当BD=BE时,BD=BE=12,CD=BC-BD=8,
CP=2CD=10; 当BD= ED时,可知点D是Rt△CBE斜边的中线,得出CD=BC=10,CP=CD=,当DE=BE时,作EH⊥BC,则H是BD中点, EH∥AB ,求出AE==9, CE=AC-AE=16,CH=20-BH,由EH∥AB, 根据平行线分线段成比例求出BH=,BD=2BH=, CD=BC- BD= , 则CP=CD=7.
24.【答案】(1)解:AC⊥CF
证明:∵矩形ABCD∽矩形CEFG
∴ ,
∵∠B=∠E=90°,
∴△ABC∽△CEF,
∴∠ACB=∠CFE,
∵∠CFE+∠FCE=90°,
∴∠ACB+∠FCE=90°,
∴∠ACF=90°,
∴AC⊥CF
(2)解:∵△ABC∽△CEF,
∴
(3)解:连接AC,
∵∠ABC=90°,AB=3,BC=4,
∴AC= ,
∵CF=10,AF=5 ,
∴ ,
∴∠ACF=90°,
tan∠AFC=
(4)解:过点F作FD⊥BC,交BC延长线于点D,
∵∠ACB+∠BAC=90°,∠ACB+∠FCD=90°,
∴∠BAC=∠FCD,
∵∠ABC=∠D,
∴△ABC∽△CDF,
∴ ,
∵AB=3,BC=4,AC=5,CF=10,
∴CD=6,FD=8,BD=10,
BF=
【解析】【分析】(1)先证出 △ABC∽△CEF, 得到 ∠ACB=∠CFE, 即可得出 AC⊥CF ;
(2)由(1)列出比例式即可求出比值为;
(3)连接AC,勾股定理求出AC,用勾股定理逆定理证明△ACF是直角三角形,按照三角函数的意义求值即可;
(4)过点F作FD⊥BC,交BC延长线于点D, 求出DF、CD即可求出BF。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2022-2023相似三角形提升卷(含解析)
一、单选题
1.若,则的值为( )
A. B. C. D.
2.下列结论中,不正确的是( )
A.若,则 B.若,则
C.若(b﹣d≠0),则 D.若,则a=3,b=4
3.下列格点三角形中,与右侧已知格点相似的是( )
A. B.C. D.
4.若矩形ABCD∽矩形EFGH,相似比为2∶3,已知AB=3 cm,BC=5 cm,则矩形EFGH的周长是( )
A.16 cm B.12 cm C.24 cm D.36 cm
5.如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )
A. B.
C. D.
6.已知的三边长是,,2,则与相似的三角形的三边长可能是( )
A.1,, B.1,, C.1,, D.1,,
7.如图,,直线与这三条平行线分别交于点A、B、C和点D、E、F,若,则DE的长度是( )
A. B. C.6 D.10
8.下列语句中,正确的有( )
①相等的圆心角所对的弧相等;
②等弦对等弧;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3;
④已知线段AB=2,点C是AB的黄全分割点,则;
⑤三角形的外心到三角形的三边距离相等.
A.1个 B.2个 C.3个 D.4个
9.如图,已知△ABC和△A′B′C′相似,则图中角度 和边长x分别为( )
A.30°,9 B.30°,6 C.40°,9 D.40°,6
10. 如图,平行四边形OABC的顶点O(0,0),A(1,2),点C在x轴的正半轴上,延长BA交y轴于点D.将△ODA绕点O顺时针旋转得到△OD'A',当点D的对应点D'落在OA上时,D'A'的延长线恰好经过点C,则点B的坐标为( )
A.(2
,2) B.(2
,2) C.(2
1,2) D.(2
1,2)
二、填空题
11.如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示__ .
12.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 .
13.如图,在⊙O中, = ,AB=10,BC=12,D是 上一点,CD=5,则AD的长为 .
14.如图,在矩形ABCD中,AD>AB,AB=2.点E在矩形ABCD的边BC上,连结AE,将矩形ABCD沿AE翻折,翻折后的点B落在边AD上的点F处,得到矩形CDFE.若矩形CDFE与原矩形ABCD相似,则AD的长为 .
15.如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处,其他顶点在矩形 ABCD 的边上; L 型中的正方形有三个顶点恰好在矩形
ABCD 的边上,另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形
ABCD相似,则 AB:BC 的值为 .
16.如图,在直角 ABC中,∠C=90°,AC=8,BC=6,点M从点C出发沿线段CA向点A移动,连接BM,MN BM交边AB于点N.若CM=2,那么线段AN= ;当点M从点C移动到AC的中点时,则点N的运动过程中路径长为 。
三、解答题
17.已知线段a,b满足 ,且a+b=14,
(1)求a,b,c的值;
(2)若线段x是线段b,c的比例中项,求x的值.
18.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.
19.如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的⊙O经过点C,交AB于点E,且AC=AE,CF为⊙O的直径,连接FE并延长交BC于点G,连接AF。
(1)求证:四边形ADGF是平行四边形;
(2)若AF:BC=3:8,BE=4,求⊙O的直径。
20.在 中, , 垂直平分 ,分别交 于点 .
(1)求证: ;
(2)求证: .
21.在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)用含t的代数式表示:线段PO= cm;OQ= cm.
(2)当t为何值时△POQ的面积为6cm2?
(3)当△POQ与△AOB相似时,求出t的值.
22.如图,已知在平面直角坐标系xOy中,抛物线y=(x﹣2)2的顶点为C,与y轴正半轴交于点B,一次函数y=kx+4(k≠0)图象与抛物线交于点A、点B,与x轴负半轴交于点D,若AB=3BD.
(1)求点A的坐标;
(2)联结AC、BC,求△ABC的面积;
(3)如果将此抛物线沿y轴正方向平移,平移后的图象与一次函数y=kx+4(k≠0)图象交于点P,与y轴相交于点Q,当PQ∥x轴时,试问该抛物线平移了几个单位长度?
23.如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .
(1)当 时,
①若 ,求 的度数;
②求证 ;
(2)当 , 时,是否存在点P,使得 是等腰三角形,若存在,求出所有符合条件的 的长.
24.如图
如图1,把两个相似比为 的矩形ABCD与矩形CEFG拼成如图所示的图案.
(1)(一)问题发现:
请探究AC与CF的位置关系并证明.
(2)求 的值.
(3)(二)拓展应用:
如图2,在四边形ABCF中,已知∠ABC=90°,AB=3,BC=4,CF=10,AF=5 .
连接BF,求BF的长.
答案解析部分
1.【答案】D
【解析】【解答】解:∵,
∴x=y,
∴,
故答案为:D.
【分析】由已知条件可得x=y,然后代入中化简即可.
2.【答案】D
【解析】【解答】解:A、若,则,而,,不合题意;
B、若,则6(a﹣b)=b,故6a=7b,则,不合题意;
C、若(b﹣d≠0),则,则,不合题意;
D、若,设,当k=1时,有a=3,b=4,当k≠1, a,b的值不是3与4,符合题意.
故答案为:D.
【分析】根据比例的性质逐项判断即可。
3.【答案】A
【解析】【解答】解:的三边长分别为:,
,,
∵,
∴为直角三角形,B,C选项不符合题意,排除;
A选项中三边长度分别为:2,4,,
∴,
A选项符合题意,
D选项中三边长度分别为:,,,
∴,
故答案为:A.
【分析】根据相似三角形的判定方法逐项判断即可。
4.【答案】C
【解析】【解答】∵AB=3cm,BC=5cm,
∴矩形ABCD的周长=2×(3+5)=16cm,
∵矩形ABCD∽矩形EFGH,相似比为2:3,
∴矩形ABCD与矩形EFGH的周长比2:3,
∴矩形EFGH的周长为24cm,
故答案为:C.
【分析】先求出矩形ABCD的周长为16cm,再求出矩形ABCD与矩形EFGH的周长比2:3,最后计算求解即可。
5.【答案】C
【解析】【解答】解:∵DE∥BC,
∴ ,
∴ ,故A选项错误,不符合题意;
,故B选项错误,不符合题意;
,故C选项正确,符合题意;
∴ ,故D选项错误,不符合题意.
故答案为:C.
【分析】易证△ADE∽△ABC,然后根据相似三角形的对应边成比例、相似三角形的周长之比等于相似比,面积之比等于相似比的平方进行判断.
6.【答案】A
【解析】【解答】解:∵△ABC三边长是,,2,
∴△ABC三边长的比为:2:=1::,
∴△ABC相似的三角形三边长可能是1::,
故答案为:A.
【分析】根据相似三角形对应边的比相等进行解答即可.
7.【答案】C
【解析】【解答】解:由平行线分线段成比例可知
∴
解得
故答案为:C.
【分析】根据平行线分线段成比例的性质可得,再将数据代入计算即可。
8.【答案】A
【解析】【解答】解:①在同圆或等圆中,相等的圆心角所对的弧相等,原说法错误,故不符合题意;
②在同圆或等圆中,等弦所对的优弧相等,等弦所对的劣弧相等,原说法错误,故不符合题意;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3,原说法正确,故符合题意;
④已知线段AB=2,点C是AB的黄全分割点,
则或,原说法错误,故不符合题意;
⑤三角形的外心到三角形的三个顶点距离相等,原说法错误,故不符合题意.
故答案为:A.
【分析】根据弧、弦、圆心角的关系,相似多边形的性质、黄全分割点、三角形的外心的性质分别进行判断即可.
9.【答案】C
【解析】【解答】解:由题意:△ABC∽△A′B′C′,
∴∠ =∠ =40°,
,即 ,
∴解得 ,
经检验 符合意义,是原方程的解.
故答案为:C.
【分析】根据相似三角形对应角相等可得∠α的度数,根据相似三角形对应边成比例可得x的值.
10.【答案】D
【解析】【解答】解:如图,连接A'C,AD⊥y轴,△ODA绕点O顺时针旋转得到△OD'A',
∴,
,
,
,
∵,
,
,
,
,
,
,
,
∴,
∴,
∴点B的坐标为:
,
故答案为:D.
【分析】连接A'C,AD⊥y轴,△ODA绕点O顺时针旋转得到△OD'A',由同角的余角相等可得∠DOA=∠D'CO,根据有两个角对应相等的两个三角形相似可得△ADO∽△OD'C,则可得比例式
,根据比例式求出CO,由平行四边形的性质得OC=AB,由线段的构成DB=AD+AB求得DB的值,则点B的坐标可求解.
11.【答案】△DEB
【解析】【解答】解:根据题意可得: , , ,
∴ ,
故答案为:△DEB.
【分析】利用相似三角形的判定方法判断求解即可。
12.【答案】3
【解析】【解答】解:依题意,两高脚杯中的液体部分两三角形相似,则
解得 .
故答案为:3.
【分析】依题意可知:两高脚杯中的液体部分两三角形相似,然后根据对应边成比例可得AB.
13.【答案】3+2
【解析】【解答】解:过A作AE⊥BC于E,过C作CF⊥AD于F,则∠AEB=∠CFD=90°,
∵ = , AB=10,
∴∠ACB=∠B=∠D,AB=AC=10,
∵AE⊥BC,BC=12,
∴BE=CE=6,
∴ ,
∵∠B=∠D,∠AEB=∠CFD=90°,
∴△ABE∽△CDF,
∴ ,
∵AB=10,CD=5,BE=6,AE=8,
∴ ,
解得:DF=3,CF=4,
在Rt△AFC中,∠AFC=90°,AC=10,CF=4,
则 ,
∴AD=DF+AF=3+2 .
故答案为:3+2 .
【分析】过A作AE⊥BC于E,过C作CF⊥AD于F,则∠AEB=∠CFD=90°,根据同弧或等弧所对的圆周角相等可得∠ACB=∠B=∠D,根据等弧所对的弦相等得AB=AC=10,由等腰三角形的三线合一得BE=CE=6, 利用勾股定理可得AE,证明△ABE∽△CDF,根据相似三角形的性质可得DF、CF,利用勾股定理求出AF,然后根据AD=DF+AF进行计算.
14.【答案】
【解析】【解答】∵矩形CDFE∽矩形ADCB,
∴ = ,即 = ,
整理得,AD2﹣2AD﹣4=0,
解得,AD1=1﹣ (舍去),AD2= ,
故答案为: .
【分析】根据矩形CDFE∽矩形ADCB,可得 = ,再将数据代入计算可得AD2﹣2AD﹣4=0,最后解一元二次方程即可。
15.【答案】 或
【解析】【解答】解:设大小相同的四个正方形的边长为a,DF=x,即GH=IJ=KJ=a,IH=EG=2a,
在Rt△IJH中,JH=
a,
∵四边形ABCD和四边形MEFD是矩形,四边形NBLK是矩形,
4个完全相同的小正方形组成的L型模板如图放置,
∴∠B=∠C=∠KLJ=∠EFG=∠JIH=90°,
∴∠LKJ+∠LJK=∠IJH+∠IHJ=∠GHC+∠HGC=∠EGF+∠GEF=90°,
∠KJL+∠IJH=∠IHJ+∠GHC=∠EGF+∠HGC=90°,
∴∠KJL=∠IHJ=∠HGC=∠GEF,
∴△KJL≌△HGC,△JHI∽△HGC∽△GEF,
∴BL=KL=HC,LJ=GC,
,
,
即
,
,
∴FG=
,EF=
,BL=KL=HC=
,LJ=GC=
,
∴CD=DF+FG+GC=x+
=
,
BC=BL+LJ+JH+HC=
+
=
,
当矩形MEFD∽矩形 ABCD时,
,即
,
解得:x=
,
AB:BC 的值为
;
当矩形MDFE∽矩形 ABCD时,
,即
,
解得:x=
(负值已舍),
AB:BC 的值为
;
故答案为:
或
.
【分析】设大小相同的四个正方形的边长为a,DF=x,即GH=IJ=KJ=a,IH=EG=2a,由勾股定理得JH= a,根据矩形的性质得∠B=∠C=∠KLJ=∠EFG=∠JIH=90°,由同角的余角相等得∠KJL=∠IHJ=∠HGC=∠GEF,证△KJL≌△HGC,△JHI∽△HGC∽△GEF,根据全等三角形的性质可得BL=KL=HC,LJ=GC,根据相似三角形的性质可得FG、EF,进而得到BL、LJ、CD、BC,根据相似矩形的对应边成比例可得x的值,进而可得AB:BC的值.
16.【答案】;
【解析】【解答】解:(1)如图,作ND⊥AC
易得AB=10
易得
∴
设ND=x,则MD=3x
则AD=AC-CM-MD=6-3x
易得
∴
∴
∴AN=
(2)同(1)理,得出AN=
故答案为:;.
【分析】由三垂直,得出,得出,设出未知数,由平行,得出,得出方程,从而得出结果。
17.【答案】(1)解:设 ,则a=3k,b=4k,c=5k,
∵a+b=14,
∴3k+4k=7k=14,
解得k=2,
∴a=6,b=8,c=10
(2)解:∵b=8,c=10,x是b,c的比例中项,
∴x2=8×10=80,
解得
【解析】【分析】(1)利用已知条件a=3k,b=4k,c=5k,根据a+b=14,可求出k的值,然后求出a,b,c的值.
(2)利用x是b,c的比例中项, 可得到x2=bc,代入可得到关于x的方程,解方程求出x的值.
18.【答案】解:设经过t秒后,△PBQ与△ABC相似,则有,,,
当时,,
即,
解得秒;
当时,,
即,
解得秒.
∴经过2.5秒或1秒时,△PBQ与△ABC相似.
【解析】【分析】分两种情况:①当时,,②当时,,再将数据代入求解即可。
19.【答案】(1)证明:连接CE.
∵AC=AE,
∴ ,
∴AD⊥CE,
∵CF是直径,
∴∠CEF=90°,
∴FG⊥CE,
∴AD∥FG,
∵CF,AD是直径,
∴∠ACD=∠CAF=90°,
∴∠CAF+∠ACD=180°,
∴AF∥BC,
∴四边形ADGF是平行四边形.
(2)解:∵∠AOF=∠COD,
∴ ,
∴AF=CD,
∵四边形ADGF是平行四边形,
∴AF=DG,
∵AF:BC=3:8,
∴BG:DG=2:3,
∵EG∥AD,
∴ ,
∵BE=4,
∴AE=AC=6,
∴AB=10,BC= =8,
∵CD=DG,BG:DG=2:3,
∴CD=GD=3,BG=2,
∴AD= =3 ,
∴⊙O的直径为3
【解析】【分析】(1)根据垂径定理得出AD⊥CE,然后根据圆周角定理求出FG⊥CE,可得AD∥FG,根据直径所对的圆周角是直角求出∠CAF+∠ACD=180°,可得AF∥BC,从而证出四边形ADGF是平行四边形.
(2) 根据平行四边形的性质和圆心角和弦的关系求出AF=CD=DG,可得BG:DG=2: 3,利用平行线分线段成比例定理求出AE、AC,再利用勾股定理求出BC、CD,即可求出结果.
20.【答案】(1)证明: ,
,
垂直平分 AB ,
,
,
,
,
;
(2)解:证明:由(1)知 ,
,
,
,
,
,
.
【解析】【分析】(1)根据等腰三角形的性质以及内角和定理可得∠ABC=∠C=72°,根据垂直平分线的性质可得AE=BE,根据等腰三角形的性质可得∠ABE=∠A=36°,推出∠BEC=∠C,据此证明;
(2)易证△BEC∽△ABC,然后根据相似三角形的性质证明即可.
21.【答案】(1)2t;(5﹣t)
(2)解:由(1)知,OP=2t cm,OQ=(5-t)cm,
∵△POQ的面积为6cm2,
∴6=×2t×(5-t),
∴t=2或3,
∴当t=2或3时,三角形POQ的面积为6cm2;
(3)解:∵△POQ与△AOB相似,∠POQ=∠AOB=90°,
∴△POQ∽△AOB或△POQ∽△BOA,
∴或,
当,则,
∴t=;
当时,则,
∴t=1,
∴当t=或1时,△POQ与△AOB相似.
【解析】【解答】(1)解:由题意知,OP=2t cm,BQ=t cm,
∴OQ=(5-t)cm,
故答案为:2t,(5-t);
【分析】(1)由题意知,OP=2t cm,BQ=t cm,则OQ=(5-t)cm;
(2)由(1)可得S==6 ,解之可得t;
(3)由题意可知 △POQ与△AOB相似分为两种情况,△POQ∽△AOB和△POQ∽△BOA,可根据相似三角形的性质对应线段成比例求出t的值。
22.【答案】(1)解:作AE⊥x轴与点E,则BO∥AE,
将x=0代入y=(x﹣2)2得y=4,
∴点B坐标为(0.4).
∵AB=3BD,
∴.
∴AE=4BO=16,
将y=16代入y=(x﹣2)2得16=(x﹣2)2,
解得x=6或x=﹣2(舍),
∴点A坐标为(6,16).
(2)作CF∥y轴交AB于点F,
将(6,16)代入y=kx+4得16=6k+4,
解得k=2,
∴y=2x+4,
将x=2代入y=2x+4得y=8,
∴点F坐标为(2,8),
∴FC=8,
∴S△ABC=S△BCF+S△ACF= FC (xC﹣xB)+FC (xA﹣xC)=×8×(2﹣0)+×8×(6﹣2)=24.
(3)设抛物线向上平移m个单位,则点P坐标为(0,4+m),
由题意可得P,Q关于对称轴对称,
∴点Q坐标为(4,4+m),
将(4,4+m)代入y=2x+4得4+m=8+4,
解得m=8,
∴该抛物线平移了8个单位.
【解析】【分析】(1)作AE⊥x轴与点E,先求出点B的坐标为(0,4),再根据平行线分线段成比例定理得出AE=16,再把y=16代入抛物线的解析式求出x的值,即可得出点A的坐标;
(2)作CF∥y轴交AB于点F,利用待定系数法求出直线AB的解析式,再求出点F的坐标,利用 S△ABC=S△BCF+S△ACF列式进行计算,即可得出答案;
(3)设抛物线向上平移m个单位,得出点P坐标为(0,4+m),从而得出点Q坐标为(4,4+m),再把点Q的坐标代入直线AB的解析式,求出m的值,即可得出答案.
23.【答案】(1)解:①如图,连接PD,
∵PB为直径,
∴∠PDB=90°,
∠BPD=65°,
∴∠PBD=90°-∠BPD=25°,
∵ ,
∴,
∴,
∴∠C=∠BPE-∠PBD=65°-25°=40°;
② 证明:∵,
∴∠CBP=∠EBP,
∵∠ABE+∠A=∠C+∠A=90°,
∴∠C=∠ABE,
∴∠ABP=∠ABE+∠EBP,∠APB=∠C+∠CBP,
∴∠ABP=∠APB,
∴AP=AB;
(2)解:存在,
如图,连接PD,
由AB=15,BC= 20,
由勾股定理得: AC= = =25,
∵AB.BC=AC.BE ,
即×15×20=×25×BE,
∴ BE=12,
∵BP是直径,
∴∠PDB =90° ,
∵∠ABC =90° ,
∴PD∥AB ,
∴△DCP∽△BCA ,
∴,
∴,
△BDE是等腰角形,分三种情况:
当BD= BE时,BD=BE=12,
∴CD=BC-BD=20-12=8,
∴ CP=CD=x8=10,
当BD= ED时,可知点D是Rt△CBE斜边的中线,
∴CD=BC=10,
∴CP=CD=×10=,
当DE=BE时,作EH⊥BC, 则H是BD中点,EH//AB, 如图,
AE== =9,
:.CE=AC-AE=25-9=16, CH=BC-BH=20-BH ,
∵EH∥AB,
∴,
即,
解得: BH= ,
∴BD=2BH=,
∴CD= BC-BD=20-=,
∴CP=CD=,
综上所述,△BDE 是等腰三角形,符合条件的CP的长为10或或7.
【解析】【分析】(1)如图,连接PD,
① 根据直径所对的圆周角是直角,结合求得∠BPD的大小,则度数可求,从而求出的度数,最后利用三角形外角的性质求出∠C的度数即可;
② 由弧相等得角相等,再由余角的性质得∠C=∠ABE,于是角的关系即可得出∠ABP=∠APB,从而证出AP=AB;
(2)由勾股定理得AC=25,由面积公式得出AB BC=AC BE,求出BE=12,连接DP,则PD∥AB,得出△DCP∽△BCA,求出CP==,CD,
△BDE是等腰三角形,分三种情况讨论,当BD=BE时,BD=BE=12,CD=BC-BD=8,
CP=2CD=10; 当BD= ED时,可知点D是Rt△CBE斜边的中线,得出CD=BC=10,CP=CD=,当DE=BE时,作EH⊥BC,则H是BD中点, EH∥AB ,求出AE==9, CE=AC-AE=16,CH=20-BH,由EH∥AB, 根据平行线分线段成比例求出BH=,BD=2BH=, CD=BC- BD= , 则CP=CD=7.
24.【答案】(1)解:AC⊥CF
证明:∵矩形ABCD∽矩形CEFG
∴ ,
∵∠B=∠E=90°,
∴△ABC∽△CEF,
∴∠ACB=∠CFE,
∵∠CFE+∠FCE=90°,
∴∠ACB+∠FCE=90°,
∴∠ACF=90°,
∴AC⊥CF
(2)解:∵△ABC∽△CEF,
∴
(3)解:连接AC,
∵∠ABC=90°,AB=3,BC=4,
∴AC= ,
∵CF=10,AF=5 ,
∴ ,
∴∠ACF=90°,
tan∠AFC=
(4)解:过点F作FD⊥BC,交BC延长线于点D,
∵∠ACB+∠BAC=90°,∠ACB+∠FCD=90°,
∴∠BAC=∠FCD,
∵∠ABC=∠D,
∴△ABC∽△CDF,
∴ ,
∵AB=3,BC=4,AC=5,CF=10,
∴CD=6,FD=8,BD=10,
BF=
【解析】【分析】(1)先证出 △ABC∽△CEF, 得到 ∠ACB=∠CFE, 即可得出 AC⊥CF ;
(2)由(1)列出比例式即可求出比值为;
(3)连接AC,勾股定理求出AC,用勾股定理逆定理证明△ACF是直角三角形,按照三角函数的意义求值即可;
(4)过点F作FD⊥BC,交BC延长线于点D, 求出DF、CD即可求出BF。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
