期末专题复习图形与坐标[上学期]

期末专题复习五图形与坐标
【知识导航】
1． 确定平面上物体位置的方法：坐标法、方位与距离法、经纬度法
2． 根据坐标描出点的位置，由点的位置写出它的坐标
3． 在同一直角坐标系中，感受图形变换后点的坐标的变化
【例题分析】
1．在图4的直角坐标系中画出△ABC关于y轴对称的△A'B'C' (不写画法)，并将点A'的坐标填写在下面的横线上。
答：点A'的坐标是 。
( http: / / )
(第1题)
2．如图2，在平面直角坐标系中，三角形②、③是由三角形①依次旋转后所得的图形．
（1）在图中标出旋转中心P的位置，并写出它的坐标；
（2）在图上画出再次旋转后的三角形④．
3.如图是一张传说中的“藏宝图”,图上除标明了A﹑B﹑C三点的位置以外,并没有直接标出”宝藏”的位置,但图上注
有寻找“宝藏”的方法:把直角△ABC补
成矩形，使矩形的面积是ABC的2倍，
“宝藏”就在矩形未知的顶点处，那么
“宝藏”的位置可能是________________
_______________________(用坐标表示)
4．在平面直角坐标系中描出下列各点A（2，1），B（0，1），C（），D（6，），并将各点用线段一次连接构成一个四边形ABCD。
（1）四边形ABCD时什么特殊的四边形？
（2）在四边形ABCD内找一点P，使得△APB、△BPC、△CPD、△APD都是等腰三角形，请写出P点的坐标。
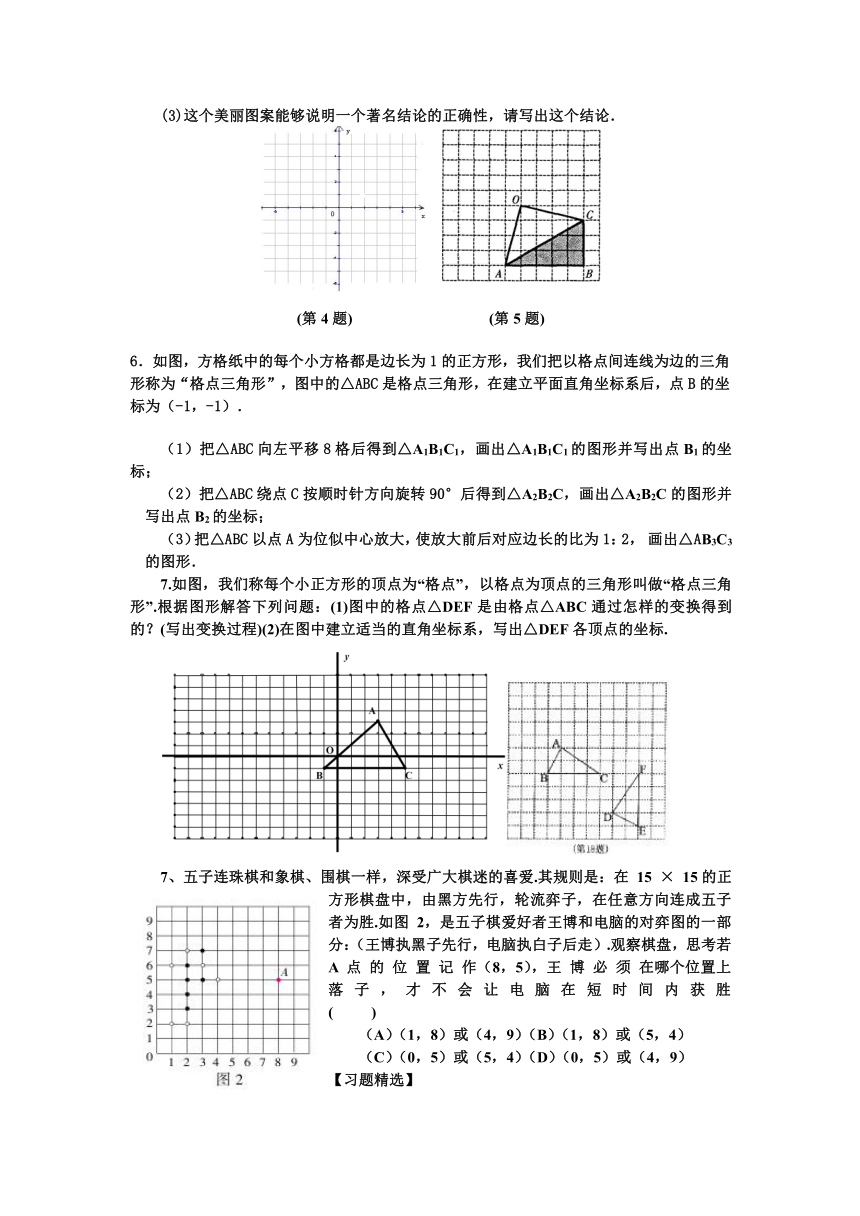
5． 如图，在网格中有一个四边形图案．
(1)请你画出此图案绕点D顺时针方向旋转900，1800，2700的图案，你会得到一个美丽的图案，千万不要将阴影位置涂错；
(2)若网格中每个小正方形的边长为l，旋转后点A的对应点依次为A1、A2、A3，求四边形AA1A2A3的面积；
(3)这个美丽图案能够说明一个著名结论的正确性，请写出这个结论．
( http: / / )
(第4题) (第5题)
6．如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC是格点三角形，在建立平面直角坐标系后，点B的坐标为（-1，-1）．
（1）把△ABC向左平移8格后得到△A1B1C1，画出△A1B1C1的图形并写出点B 1的坐标；
（2）把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C，画出△A2B2C的图形并写出点B2的坐标；
（3）把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，画出△AB 3C3的图形．
7.如图，我们称每个小正方形的顶点为“格点”，以格点为顶点的三角形叫做“格点三角形”.根据图形解答下列问题：(1)图中的格点△DEF是由格点△ABC通过怎样的变换得到的？(写出变换过程)(2)在图中建立适当的直角坐标系，写出△DEF各顶点的坐标.
HYPERLINK "http://"
7、五子连珠棋和象棋、围棋一样，深受广大棋迷的喜爱.其规则是：在 15 × 15的正方形棋盘中，由黑方先行，轮流弈子，在任意方向连成五子者为胜.如图 2，是五子棋爱好者王博和电脑的对弈图的一部分：（王博执黑子先行，电脑执白子后走）.观察棋盘，思考若 A 点 的 位 置 记 作（8，5），王 博 必 须 在哪个位置上落子，才不会让电脑在短时间内获胜 ( )
（A）（1，8）或（4，9）（B）（1，8）或（5，4）
（C）（0，5）或（5，4）（D）（0，5）或（4，9）
【习题精选】
1.在平面直角坐标系中，□ABCD的顶点A、B、D
的坐标分别是(0,0)，(5,0)，(2,3)，则顶点C的
坐标是--------------------------------（ ）
A.（3，7） B.（5，3） C.(7,3) D.(3,5)
2．如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连结OB，将纸片OABC沿OB折叠，使点A落在A’的位置上．若OB=，，求点A’的坐标为_______________．
(第2题) (第3题)
3.一青蛙在如图8×8的正方形（每个小正方形的边长为1）网格的格点（小正方形的顶点）上跳跃，青蛙每次所跳的最远距离为，青蛙从点A开始连续跳六次正好跳回到点A，则所构成的封闭图形的最大面积是 ．
4、在平面内，将一个图形沿某个方向移动一定距离，这样的图形变换为平移，如图，将网格中的三条线段沿网格线的方向（水平或垂直）平移后组成一个首位依次相接的三角形，至少需要移动
A.12格 B.11格 C.9格 D.8格
(第4题) (第5题)
5.如图，已知平面直角坐标系，A、B两点的坐标分别为A（2，－3），B（4，－1）。
（1）若P（p，0）是x轴上的一个动点，则当p=____时，△PAB的周长最短；
（2）若C（a，0），D（a+3，0）是x轴上的两个动点，则当a=____时，四边形ABDC的周长最短；
（3）设M，N分别为x轴和y轴上的动点，请问：是否存在这样的点M（m，0）、N（0，n），使四边形ABMN的周长最短？若存在，请求出m=____,n=___（不必写解答过程）；若不存在，请说明理由。
6. 如图，直角坐标系中，已知点A(2，4)，B(5，0)，动点P从B点出发沿BO向终点O运动，动点O从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了s．
(1)Q点的坐标为(＿＿＿，＿＿＿)（用含x的代数式表示）
(2)当x为何值时，△APQ是一个以AP为腰的等腰三角形
(3)记PQ的中点为G．请你探求点G随点P，Q运动所形成的图形，并说明理由.
7．如图,在10×10的正方形网格纸中,线段AB、CD的长均等于5．则图中到AB和CD所在直线的距离相等的网格点的个数有
A．2个 B．3个 C． 4个 D．5个
8．如图11，点O、B坐标分别为(0， 0)、(3， 0)，将△OAB绕O点按逆时针方向旋转90°到OA′B′；⑴画出△OA′B′；
⑵点A′的坐标为________________；⑶求BB′的长．
9.如图，在平面直角坐标系中，A点坐标为（3，4），将OA绕原点 O逆时针旋转900得到OA ，则点A 的坐标是（ ）
A、（-4，3） B、（-3，4） C、（3，-4） D、（4，-3）
y A
x
（第2题）
C(0,0)
B(0, )
(-2,0) A
A
D
C
B
第7题图