7.4 一次函数的图象(1)[上学期]
文档属性
| 名称 | 7.4 一次函数的图象(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 549.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-28 00:00:00 | ||
图片预览





文档简介
课件13张PPT。7.4 一次函数的图象金山学校 吴国凤创设情境为迎接校运动会,甲、乙两位
学生进行跑步训练。右边的图
象表示的是甲、乙两人在一次
赛跑中路程s与时间t的函数图
象。根据图象回答下列问题:o25100501263xy(1)这是一次几百米的赛跑?(2)甲、乙两人中谁先到达终点?(3)乙在这次赛跑中的速度是多少?探究新知 以右图图象甲为例:
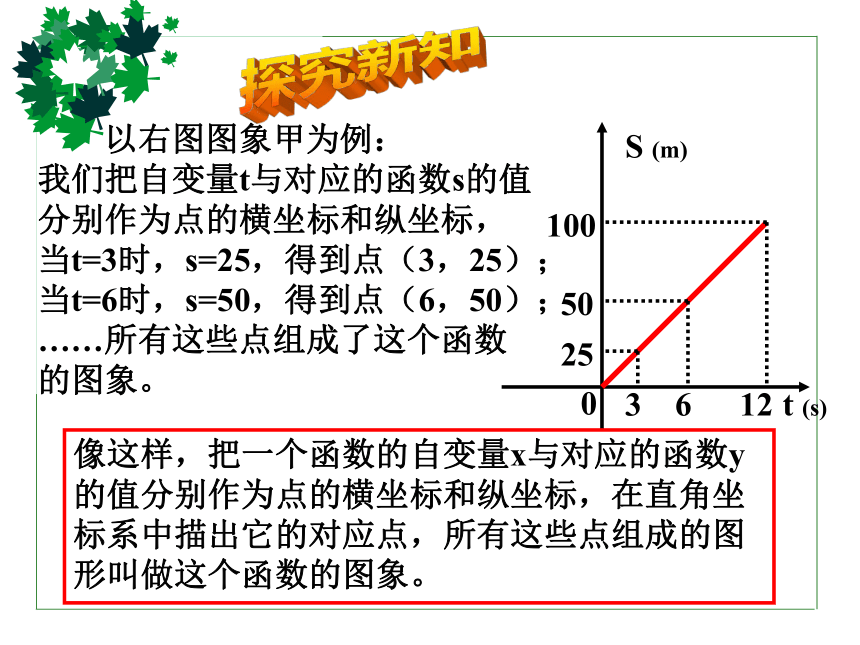
我们把自变量t与对应的函数s的值分别作为点的横坐标和纵坐标,当t=3时,s=25,得到点(3,25);当t=6时,s=50,得到点(6,50);
……所有这些点组成了这个函数的图象。036122550100t (s)S (m)像这样,把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象。活动一:作一次函数y=2x的图象。 根据概念作如下探究:
(1)分别选择若干对自变量与函数的对应值,
列成下表:- 4- 2024(2)分别以表中的x值作点的横坐标,对应的
y值作纵坐标得到一组点:
(- 2 , - 4 ), ( - 1, - 2 ), ( 0 , 0 ), ( 1 , 2 ) ,( 2, 4 )(3)画直角坐标系,并在直角坐标系中画出相应的点(4)观察所画的点,发现了什么?把你的发现与同
伴交流。要求师生共同完成活动二:作一次函数y=2x+1的图象。请同学们根据上面的画图步骤,自己动手尝试作一次函数y=2x+1的图象。
(要求与一次函数y=2x的图象在同一直角坐标系内)活动三:议一议(1)如右图,坐标满足一次函数y=2x的各点(-2, -4), ( -1, -2 ), ( 0, 0), ( 1,2) , ( 2, 4 )……都在直线上 l1上吗?坐标满足y=2x+1的各点(-2,-3),(-1,-1 ),( 0,1),( 1,3 ),( 2,5 )
……都在直线上 l2上吗?xy012345-1-2-3-4-512345-1-2-3-4-5反过来,在直线l1上取一些点,这些点的坐标都分别满足y=2x吗?在直线l2上取一些点,这些点的坐标都分别满足y=2x+1吗?归纳新知一次函数y=kx+b(k,b都为常数,k≠0)可以用直角坐标系中的一条直线来表示,这条直线叫做一次函数y=kx+b的图象。应用新知例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标系。
y =3x , y= -3x + 2问题1:y=3x , y=-3x+2两函数的图象是什么图象?问题2:在平面直角系中确定一条直线需要几个点?问题3:你会找哪两个点?和你的同学讨论,取哪些点画图时比较方便?xy例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标系。
y =3x , y= -3x + 2书山求道0123123-3-2-1-1-24(0,0)(1,3)(0,2)(1,-1)想一想你能直接利用函数解析式
求函数图象与坐标轴交点的坐标吗?y =3xy= -3x + 2随堂练习1、函数y=2x+3的图象是( )
(A)过点(0,3 ),(0, )的直线。
(B)过点(0, ),(1, 5)的直线。
(C)过点( ,0),(-1, 1)的直线。
(D)过点( 0,3),( ,0)的直线。2、在同一直角坐标系中画出下列函数的图象,并标出它们与坐标轴的交点:
y= x , y= x+2 , y= x+2 感悟反思知识整理1、如何画函数的图象?画函数的图象的一般步骤是什么?2、一次函数的图象是什么?如何简便地画出一次函数的图象?3、函数的图象是研究和处理有关函数问题的重要工具,也是数形结合思想的充分体现。这节课,你有什么收获,能与我们一起分享吗? 精选作业1、作业本
2、课后作业
学生进行跑步训练。右边的图
象表示的是甲、乙两人在一次
赛跑中路程s与时间t的函数图
象。根据图象回答下列问题:o25100501263xy(1)这是一次几百米的赛跑?(2)甲、乙两人中谁先到达终点?(3)乙在这次赛跑中的速度是多少?探究新知 以右图图象甲为例:
我们把自变量t与对应的函数s的值分别作为点的横坐标和纵坐标,当t=3时,s=25,得到点(3,25);当t=6时,s=50,得到点(6,50);
……所有这些点组成了这个函数的图象。036122550100t (s)S (m)像这样,把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象。活动一:作一次函数y=2x的图象。 根据概念作如下探究:
(1)分别选择若干对自变量与函数的对应值,
列成下表:- 4- 2024(2)分别以表中的x值作点的横坐标,对应的
y值作纵坐标得到一组点:
(- 2 , - 4 ), ( - 1, - 2 ), ( 0 , 0 ), ( 1 , 2 ) ,( 2, 4 )(3)画直角坐标系,并在直角坐标系中画出相应的点(4)观察所画的点,发现了什么?把你的发现与同
伴交流。要求师生共同完成活动二:作一次函数y=2x+1的图象。请同学们根据上面的画图步骤,自己动手尝试作一次函数y=2x+1的图象。
(要求与一次函数y=2x的图象在同一直角坐标系内)活动三:议一议(1)如右图,坐标满足一次函数y=2x的各点(-2, -4), ( -1, -2 ), ( 0, 0), ( 1,2) , ( 2, 4 )……都在直线上 l1上吗?坐标满足y=2x+1的各点(-2,-3),(-1,-1 ),( 0,1),( 1,3 ),( 2,5 )
……都在直线上 l2上吗?xy012345-1-2-3-4-512345-1-2-3-4-5反过来,在直线l1上取一些点,这些点的坐标都分别满足y=2x吗?在直线l2上取一些点,这些点的坐标都分别满足y=2x+1吗?归纳新知一次函数y=kx+b(k,b都为常数,k≠0)可以用直角坐标系中的一条直线来表示,这条直线叫做一次函数y=kx+b的图象。应用新知例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标系。
y =3x , y= -3x + 2问题1:y=3x , y=-3x+2两函数的图象是什么图象?问题2:在平面直角系中确定一条直线需要几个点?问题3:你会找哪两个点?和你的同学讨论,取哪些点画图时比较方便?xy例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标系。
y =3x , y= -3x + 2书山求道0123123-3-2-1-1-24(0,0)(1,3)(0,2)(1,-1)想一想你能直接利用函数解析式
求函数图象与坐标轴交点的坐标吗?y =3xy= -3x + 2随堂练习1、函数y=2x+3的图象是( )
(A)过点(0,3 ),(0, )的直线。
(B)过点(0, ),(1, 5)的直线。
(C)过点( ,0),(-1, 1)的直线。
(D)过点( 0,3),( ,0)的直线。2、在同一直角坐标系中画出下列函数的图象,并标出它们与坐标轴的交点:
y= x , y= x+2 , y= x+2 感悟反思知识整理1、如何画函数的图象?画函数的图象的一般步骤是什么?2、一次函数的图象是什么?如何简便地画出一次函数的图象?3、函数的图象是研究和处理有关函数问题的重要工具,也是数形结合思想的充分体现。这节课,你有什么收获,能与我们一起分享吗? 精选作业1、作业本
2、课后作业
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
