７．４一次函数的图象[上学期]

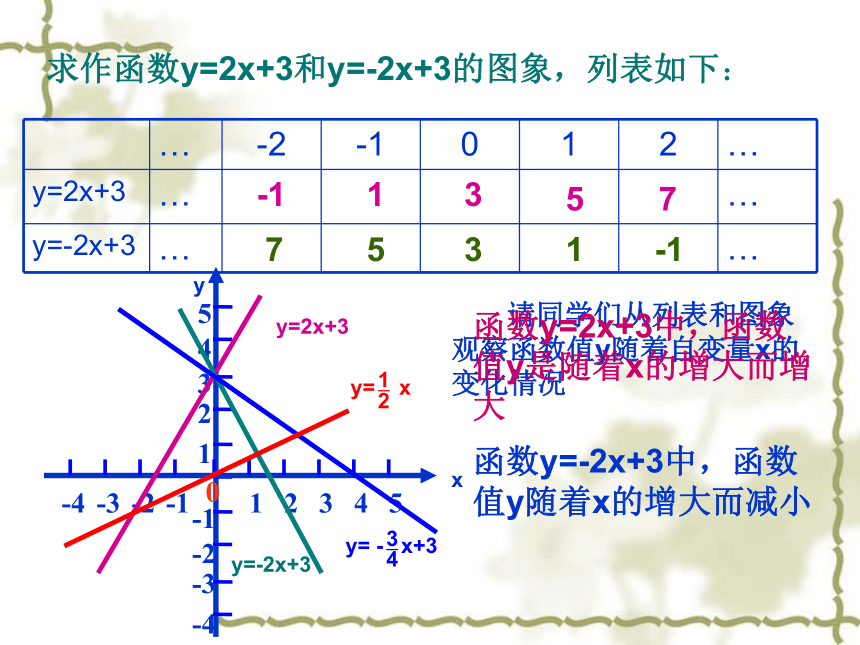
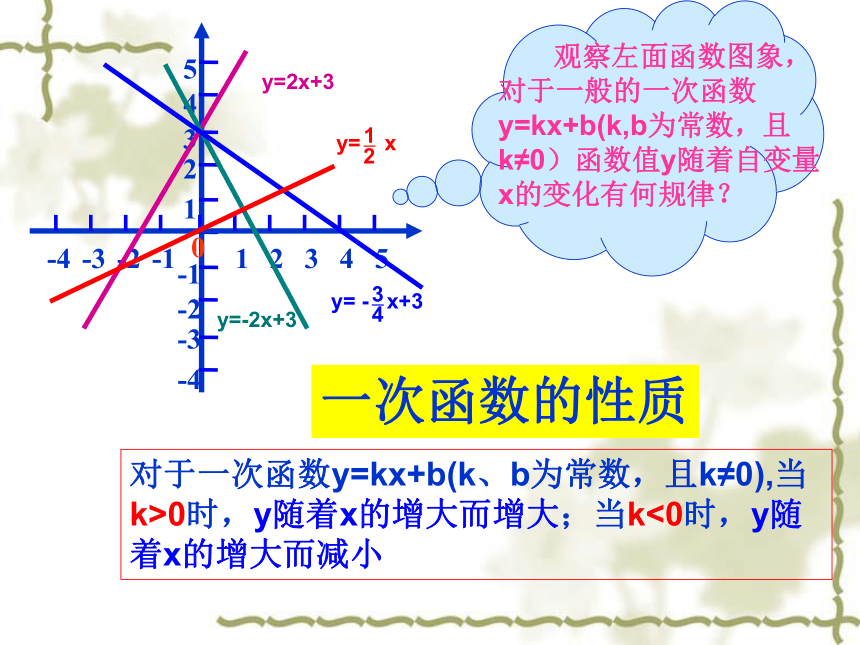
课件29张PPT。7.4一次函数的图象（二）求作函数y=2x+3和y=-2x+3的图象，列表如下：y=2x+3y=-2x+3 请同学们从列表和图象观察函数值y随着自变量x的变化情况-113577531-1函数y=2x+3中，函数值y是随着x的增大而增大函数y=-2x+3中，函数值y随着x的增大而减小yx一次函数的性质对于一次函数y=kx+b(k、b为常数，且k≠0),当k>0时，y随着x的增大而增大；当k<0时，y随着x的增大而减小y=2x+3y=-2x+3学 以 致 用下列函数,y的值随着x值的增大如何变化？做一做1.设下列两个函数当 x = x1时，y = y1；
当x = x 2时，y = y2，用“<”或“>”号填空
①对于函数y= x,若x2>x1,则y2___y1
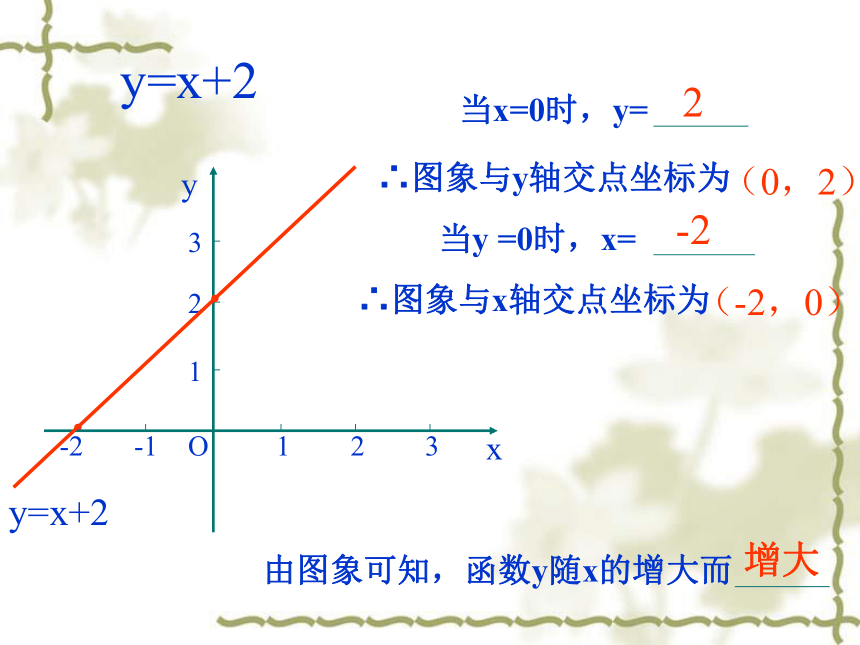
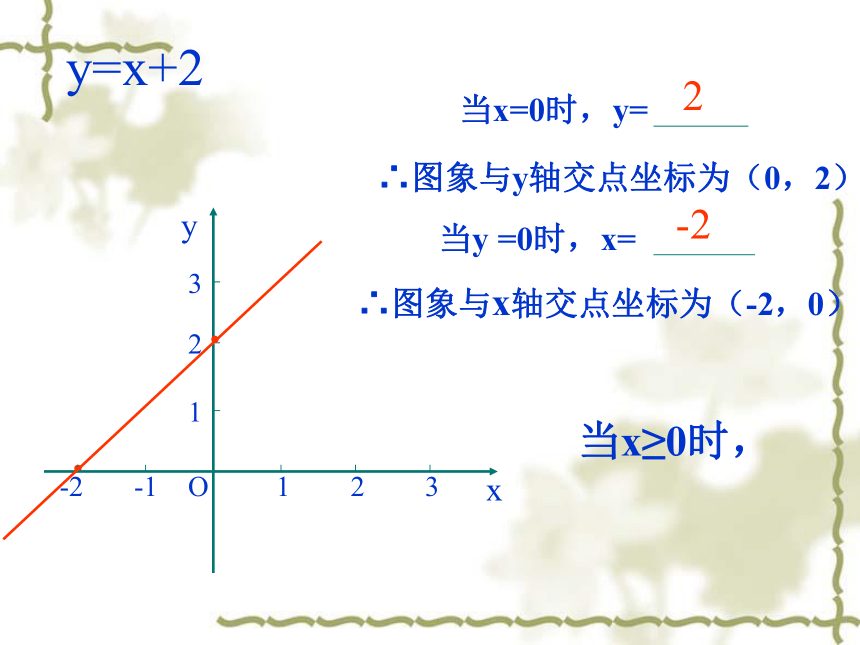
②对于函数y= - x+3,若x2___x1,则y2>（３）直线y= 　　x+m上有点A(-1, y1 ),B( ,y2),C(1,y3)则y1, y2,y3的大小 ___ 做一做：y=x+2··∴图象与y轴交点坐标为∴图象与x轴交点坐标为2-2增大（0，2）（-2，0）y=x+2··∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当x≥0时，2-2y=x+2··∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当x≥0时，2-2y=x+2·xyO123123-1-2·∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当x≤2时，2-24·y=x+2·xyO123123-1-2·∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当0 ≤x≤2时，2-245·y=x+2·xyO123123-1-2·∴图象与y轴交点坐标为（0，2）∴图象与x轴交点坐标为（-2，0）当0 ≤x≤2时，2-245·例1：已知一次函数 的函数值y随自变量x的增大而增大，求m的取值范围。y=(m-1)xm2-31、一次函数y=(2m+1)x+2m的图象不
经过第二象限，求m的取值范围.2.已知：一次函数y=kx+(k2-3)的图象过点（０，３）且y随x的增大而减少，求k的取值范围.
2.函数y=kx+1的图象如图所示，则 k____0xy10则m是（ ）(A). M<-1 ( B). M>-1 (C). M=1 (D). M<1A做一做：某函数具有下列两个性质：
（1）它的图象是经过点（－1，2）的一条直线；（2）函数值随自变量的增大而减小；请写出符合上述条件的一个函数解析式：___________已知：一次函数y=kx-5的图象与两坐标轴围成的面积为13，且函数y的值随x的增大而增大，求此一次函数的解析式。2.小明参加100米短跑训练，一星期内训练天数与成绩的关系如图所示（1）小明训练3天后，它的成绩是多少？提高了还是降低了？（2）这7天中的最好的成绩是多少？9631215182124y/cml2468101214t/天3.某植物栽种t天后的高度为ycm,图中的l 反映了y与t之间的关系，根据图象回答下列问题：(1)植物刚栽的时候多高？（2）3天后该植物高度为多少？（3）几天后植物高度可达21cm?0我国的水资源丰富，并且得到了较好的开发，电力充足，某供电公司为了鼓励居民用电，采用分段计费的方法计算电费，月用电量x度与相应电费y元之间的函数关系的图象如图所示（1）月用电量为100度时，应交电费是多少？（2）当x≥ 100时，y与x之间的函数关系式是什么？（3）月用电量为260度时，应交电费多少元？一次函数的图象和性质小结：过(0,b)的直线
过(0,0)的直线
k＞0
k＜0y随x的增大而增大
y随x的增大而减小
4、一次函数y=kx+b的图象如图所示，则
k 0,b 0 挑 战 自 己xyo<<挑 战 自 己1、y=x+1与坐标轴的交点坐标？
2、y=(-3 k+1) x+2 k-1的图象
经过原点，确定k的值？3、写出m的3个值，使相应的一次
函数y=(2m-1)x+2的值都是随着x值
的增大而减小.例2 我国某地区现有人工造林面积12万公顷，规划今后10年新增造林61000～62000公顷，请估算6年后该地区的造林总面积达到多少万公顷思考(1)：从题目的已知条件中，假设P表示今后10年平均每年造林的公顷数，则P的取值范围是___________6100≤P≤6200思考(2):假设6年后造林总面积为S（公顷），那么如何用P来表示S呢？S=6P+120000思考(3)： S=6P+120000 这是一个一次函数。那么函数值s随着自变量p的增大而增大？还是增大而减小？ ∵k=6>0 ∴ y随着x的增大而增大6×6100+120000≤s≤6×6200+120000思考(4): 6年后该地区的造林总面积由什么来决定？例2 我国某地区现有人工造林面积12万公顷，规划今后10年新增造林61000～62000公顷，请估算6年后该地区的造林总面积达到多少万公顷解：设P表示今后10年平均每年造林的公顷数，则 6100≤P≤6200。设6年后该地区的造林面积为S公顷，则 S=6P+120000∴K=6>0 ，s随着p的增大而增大∵ 6100≤P≤6200∴6×6100+120000≤s≤6×6200+120000即：156600≤s≤157200答： 6年后该地区的造林面积达到15.66～15.72万公顷（1）对于函数y=-2x+5，当-1 A（0，-8），B（1，2）两点，求当1 函数值y的变化范围巩固练习：课堂小结： 在这节课，你的收获是什么？
（1）一次函数的性质（2）利用一次函数的性质解简单实际问题