7.4（2）一次函数的图象[上学期]

课件19张PPT。
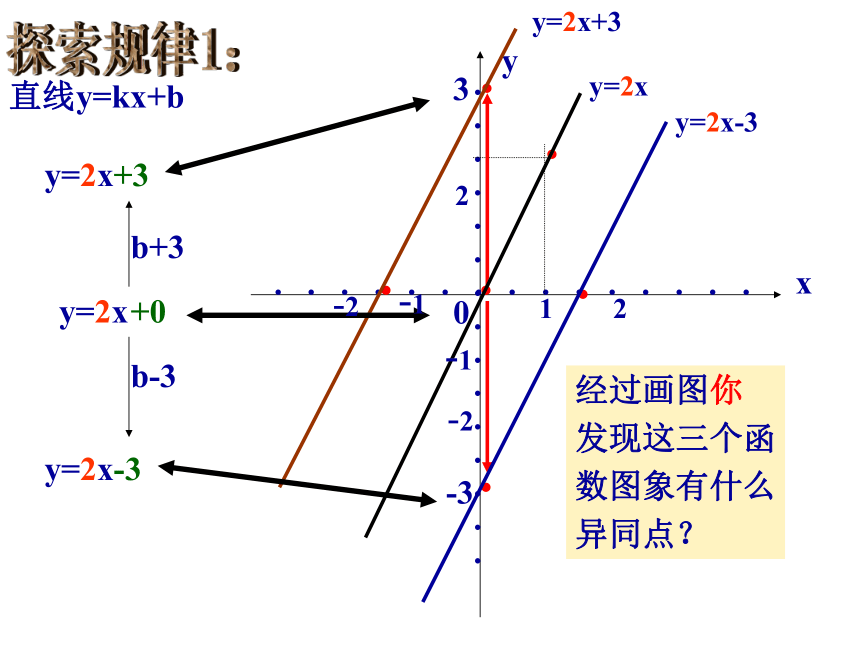
一次函数的图象和性质直线y=kx+b经过画图你
发现这三个函
数图象有什么
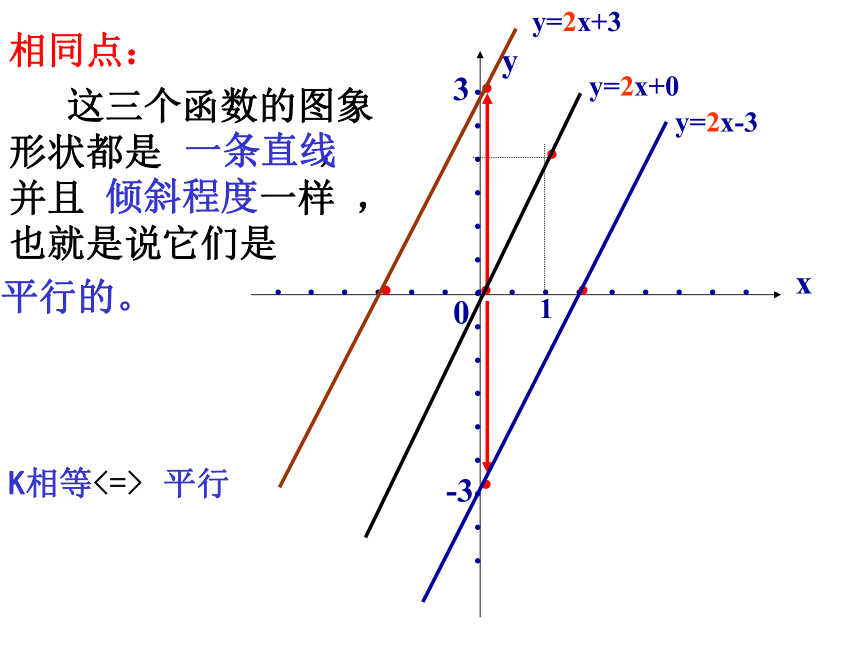
异同点？+01-33探索规律1：22-1-2-1-21-33相同点： 这三个函数的图象形状都是 ，并且 一样 ，也就是说它们是一条直线 倾斜程度平行的。K相等<=>平行1-33不同点：1.函数y=2x的图象过 (0,0) ；
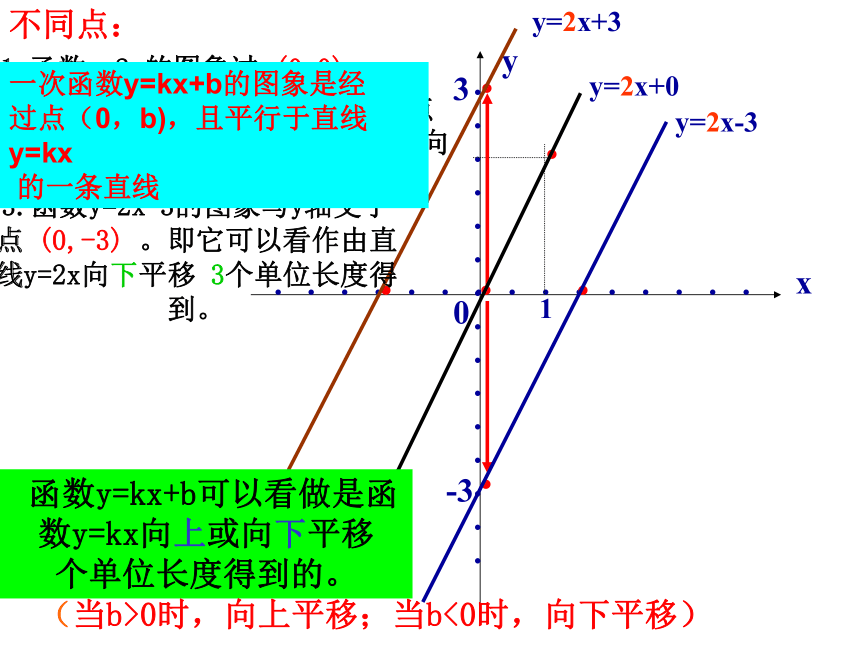
2.函数y=2x+3的图象与y轴交于点 (0,3) ，即它可以看作由直线y=2x向上平移 个单位长度得到。33.函数y=2x-3的图象与y轴交于点 (0,-3) 。即它可以看作由直线y=2x向下平移 3个单位长度得到。 函数y=kx+b可以看做是函数y=kx向上或向下平移 个单位长度得到的。（当b>0时，向上平移；当b<0时，向下平移）
一次函数y=kx+b的图象是经
过点（0，b)，且平行于直线y=kx
的一条直线巩固练习 1．把直线 的图象先向上平移
3个单位 ，得到一次函数 y = 的图
象，再向下平行移动5个单位，得到一次
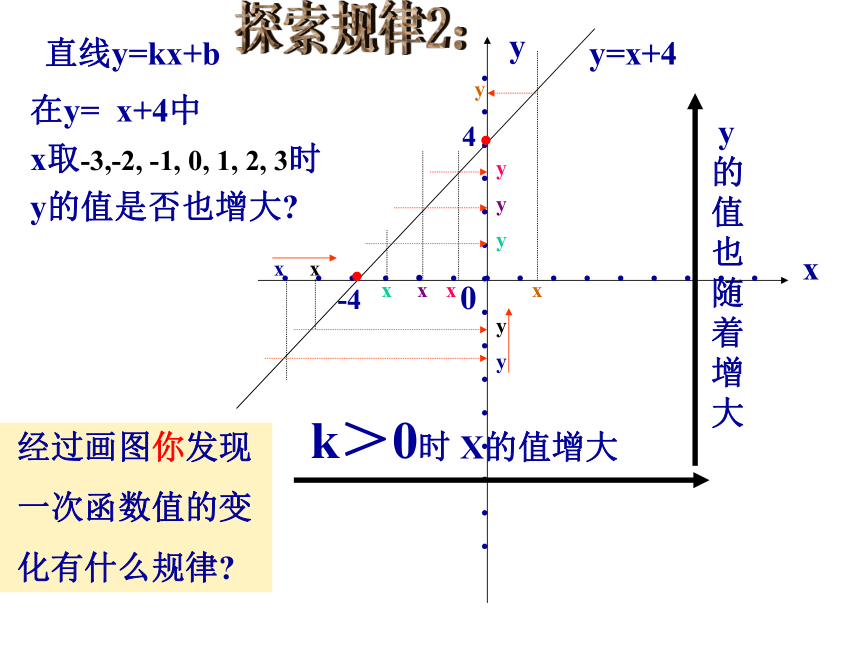
函数 y = 的图象． 2.已知直线y=(2m-1)x+m与直线y=x-2平行，且与直线y=-1/3x+2n-3交y轴于同一点，则m= ____,n=___。123.如果要通过平移直线 得到 的图象，那么直线 必须向___平移___个 单位下巩固练习直线y=kx+b在y= x+4中
x取-3,-2, -1, 0, 1, 2, 3时
y的值是否也增大?
经过画图你发现
一次函数值的变
化有什么规律?探索规律2：直线y=kx+by=-x+4
取-3,-2, -1, 0, 1, 2, 3时
y的值是否也增大?
··经过画图你发现
一次函数值的变
化有什么规律?44探索规律2：y=kx+b
(k≠0) x 取
一切实数k＞0k＜0 当k＜0时，y 随x 的增大而减小 当k＞0时，y 随x 的增大而增大
正比例函数y=kx (k≠0)y=2xy=-2x1．图象都经过原点2． 当k＞0时，图象经过第一、三象限，y随x的增大而增大 当k＜0时，图象经过第二、四象限，y随x的增大而减小探索规律3：1．图象都经过原点2． 当k＞0时，图象经过第一、三象限，y随x的增大而增大 当k＜0时，图象经过第二、四象限，y随x的增大而减小y=2x +3y=2x-3y=-2x +3y=-2x -3k>0b>0k>0b<0k<0b>0k<0b<0探索规律3： y=kx
(k≠0) 一条直线
该直线经过（0，0），
（1，k)两点 当k＜0时，图象经过第二、四象限，y随x的增大而减小y=kx+b
(k≠0) 该直线经过点（0，b），
且平行于直线 y=kx 当k＞0时，y 随x 的增大而增大
当k＜0时，y 随x 的增大而减小1．图象都经过原点2． 当k＞0时，图象经过第一、三象限，y随x的增大而增大一条直线正比例
函数一次函数1、一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。1 一次函数y=ax+b中，a＜0，b＞0，则它的图象可能是（ ） B 课堂练习： 2、看图象，确定一次函数y=kx+b(k≠0)
中k,b的符号。k<0
b<0k>0
b>0
k<0
b=0课堂练习： 课堂练习： 3 对于函数y=5x+6,y的值随x的值减小而______。减少4 函数y=2x－1经过 象限一、三、四B6 点A(-3,y1）、点B（2，y2)都在直线y=-4x+3上，则y1与y2的关系是（ ）
A y1 ≤y2　　B y1＝y2　　C y1< y2　D y1 ＞y2D-24xyo6yo24x6x6yo-24xyo6247 拖拉机开始工作时，油箱有油24升，若每时耗油
4升，则油箱中剩油量y(升)与工作时间x（时）之间的
函数关系式和图象是（ ）ABCDD课堂练习： 8．一次函数 的图象与 y 轴的交点
坐标（0，1），且平行于直线 ，求这
个一次函数的解析式． 解：∵　　　　　　 平行于直线　　又∵ 图象与 y 轴的交点坐标（0，1）课堂练习： 3、知道在直线y=k1x+b1和直线y=k2x+b2中，如果
k1=k2，那么这两条直线________，并且其中一
条直线可以看作是由另一条直线_______得到的，平行平移4、函数y = kx + b的增减性与函数y = kx 相同。同学们，本节课有那些收获？当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减少。5、k ，b的符号决定了图象的位置。2、一次函数y=kx+b(k≠0)的图象是经过点(0,b)
且平行于直线y=kx (k≠0)的一条直线。1、正比例函数y=kx (k≠0)的图象是经过点(0,0)
的一条直线。