一次函数的简单应用[上学期]

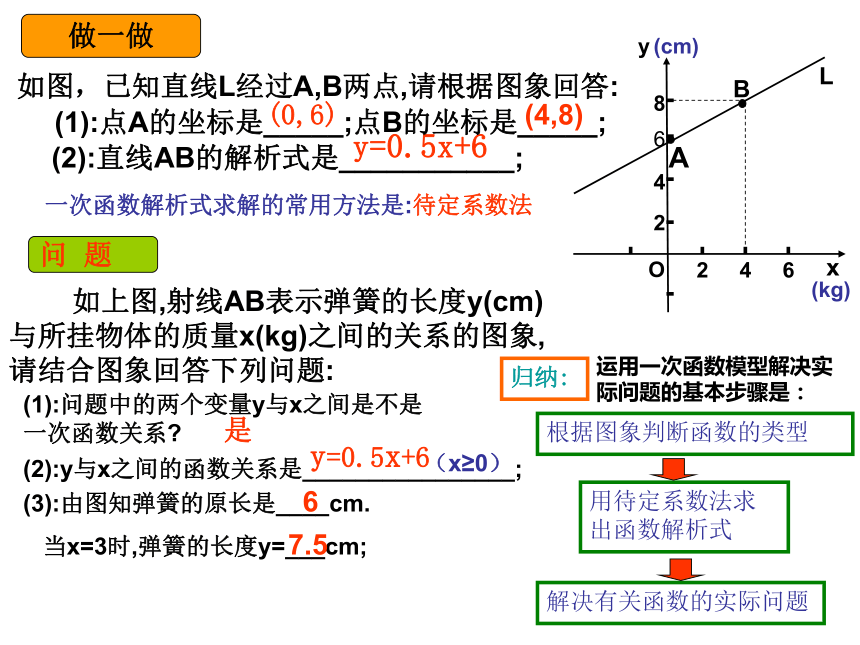
课件13张PPT。一次函数的应用 如图，已知直线L经过A,B两点,请根据图象回答:
xyO2462846ABL 如上图,射线AB表示弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系的图象,请结合图象回答下列问题:(1):问题中的两个变量y与x之间是不是一次函数关系?(2):y与x之间的函数关系是________________;(3):由图知弹簧的原长是____cm.
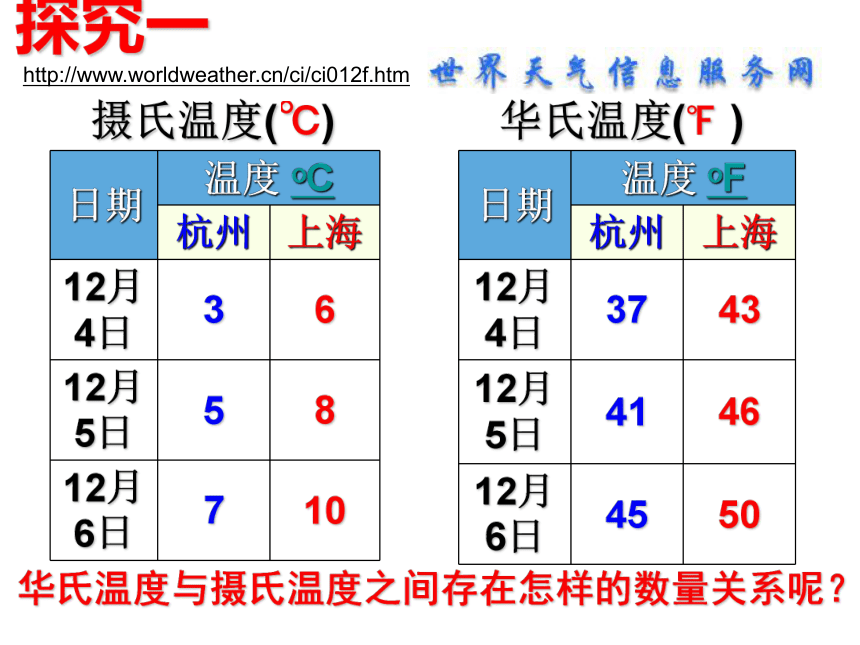
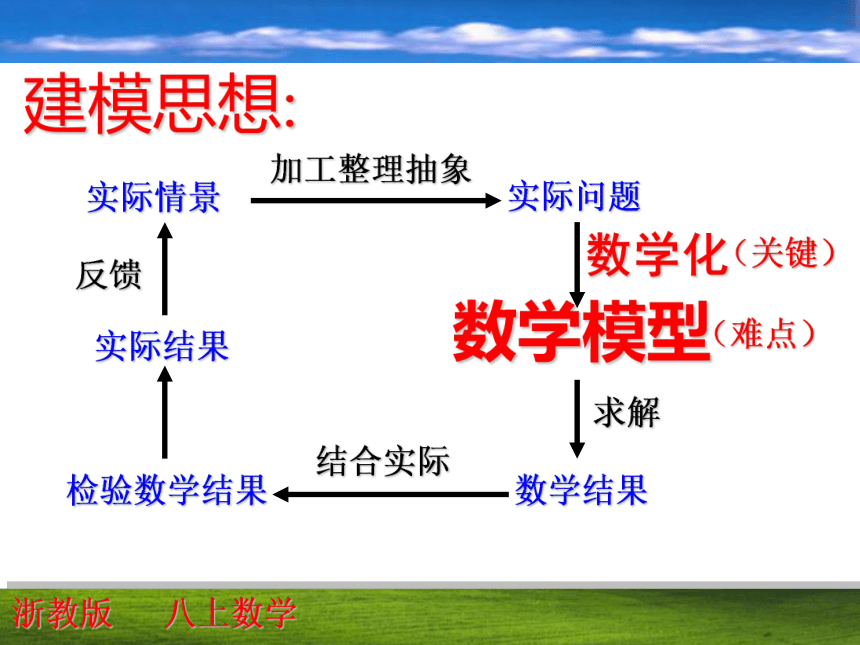
当x=3时,弹簧的长度y=___cm; (0,6)(4,8)y=0.5x+6(kg)(cm)是y=0.5x+67.5一次函数解析式求解的常用方法是:待定系数法归纳:运用一次函数模型解决实际问题的基本步骤是：6根据图象判断函数的类型用待定系数法求出函数解析式解决有关函数的实际问题（x≥0）(1):点A的坐标是_____;点B的坐标是_____;(2):直线AB的解析式是___________;做一做问 题理一理通过实验获得数据根据数据画出函数的图象根据图象判断函数的类型用待定系数法求出函数解析式解决有关函数的实际问题寻找数据间的规律得出函数的解析式运用一次函数的模型解决实际问题过程摄氏温度(℃)华氏温度(℉)http://www.worldweather.cn/ci/ci012f.htm华氏温度与摄氏温度之间存在怎样的数量关系呢？探究一建模思想:实际情景加工整理抽象数学化求解数学模型实际问题结合实际反馈检验数学结果实际结果数学结果（关键）（难点）浙教版 八上数学 实际问题数据获得描点画图猜想类型求解验证描点连线近似猜测 求解析式代入验证写出结论获取数据基本步骤： 生物学家测得7条成熟的雄性鲸的全长y和吻尖
到喷水孔的长度x的数据如下表(单位：m)：问能否用一次函数刻画这两个变量y和x的关系? 转炉炼钢产生的棕红色烟尘会污染大气，某
装置可通过回收棕红色烟尘中的氧化铁从而降低
污染，该装置的氧化铁回收率（y）与其通过的
电流（x）有关，现经过试验得到下列数据：请探究这两个变量y和x的函数关系. 富阳市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.(1):分别写出0≤x≤15和x>15时,y与x的函数关系式;
(2):若某用户该月用水21吨,则应交水费多少元?典型例题分析解题思路：关键是识别自变量在不同的取值范围内所对应函数的类型用待定系数法分别求出不同范围内的函数解析式分段函数10 20 30 40 50 60 Ot(分)S(km)12 周末小明从家里骑车去大润发超市购物，然后从超市返回家中。小明离家的路程s(km)和所经过的时间t（分）之间的函数关系如图所示，请根据图象回答下列问题：
(1):小明去超市途中的速度是多少？回家途中的速度是多少？小明在超市逗留了多少时间？(2):用恰当的方式表示小明回家的路程s(km)和所经过的时间t(分)之间的函数关系。0.2km/分0.1km/分30分钟AC∴s=- 0.1t+6(40≤t≤60)尝试园地2(3):如图,折线OABC是S与t之间的函数关系的图象,请用函数关系式表示;B 为了绿化校园,富春街道给我校送来了一棵山毛榉和一棵枫树，山毛榉高2.4m，枫树高0.9m。山毛榉的平均生长速度是每年长高0.15m，枫树的平均生长速度是每年长高0.3m.请根据上述回答下列问题:枫树山毛榉思考: 本题能否借助于一次函数的图象来解决?拓展与提高(1):分别求出枫树的生长高度y1(米) 、山毛榉的生长高度y2(米)与时间x(年)的函数关系式. (2):多少年后,两种树的树高相同?(3):多少年后枫树将比山毛榉高？图象法 如图,在边长为2的正方形ABCD的一边BC上有一点P 从B点开始运动到C点,设BP=x,四边形APDC的面积为y.(1):求y关于x的函数关系式,并写出自变量x的取值范围;(2):当x为何值时,四边形APCD的面积等于3?(3):当P点由B向C运动时,四边形APCD的面积是越来越大,还是越来越小?(4):你能说出函数y的最大值和最小值吗?ABCDP2x2-x