浙教版数学七年级上册6.8余角和补角 课件(共14张PPT)
文档属性
| 名称 | 浙教版数学七年级上册6.8余角和补角 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 644.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-27 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
6.8余角和补角
问题1:有两堵围墙,有人想测地面上形成的∠AOB 的度数,但人又不能进入围墙,只能站在墙外,怎么测量呢?
延长BO到C(延长AO到D)
只要测出∠AOC 的度数,
即可求出∠AOB 的大小.
A
O
B
C
D
α
问题2:如图:一个破损的直角三角形,已知一个角为α,求另一个锐角的度数.
2
1
A
B
O
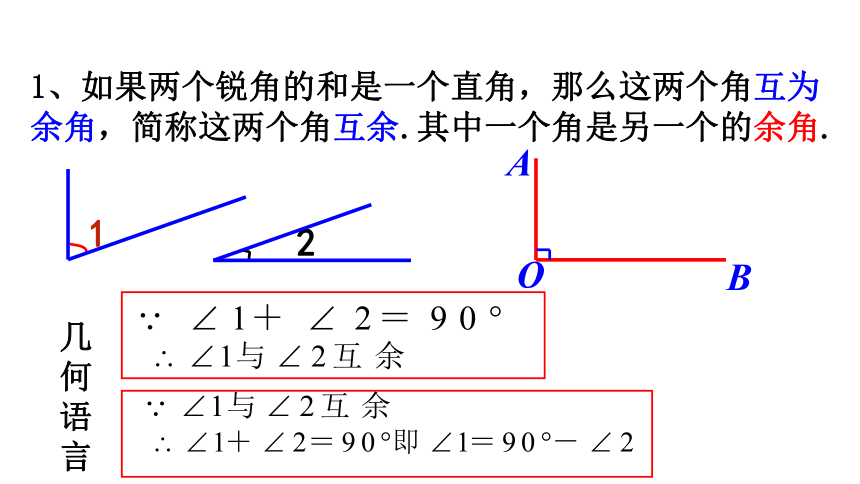
1、如果两个锐角的和是一个直角,那么这两个角互为余角,简称这两个角互余.其中一个角是另一个的余角.
几何语言
1
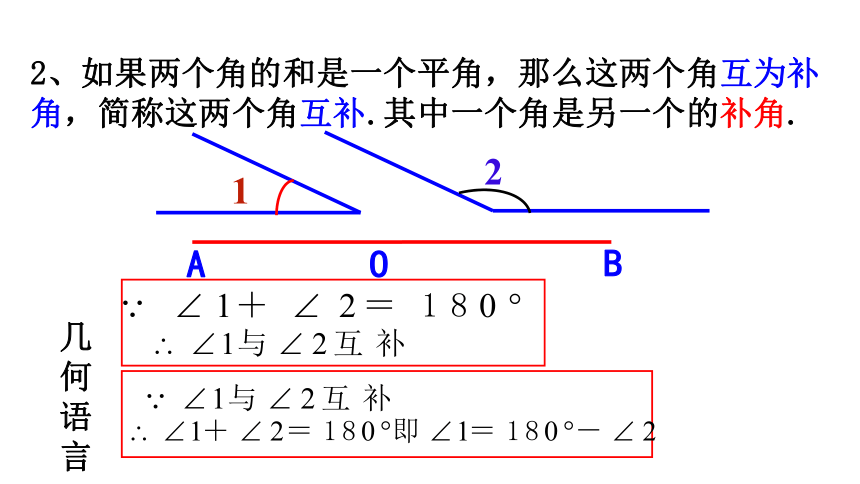
2、如果两个角的和是一个平角,那么这两个角互为补角,简称这两个角互补.其中一个角是另一个的补角.
A
B
O
几何语言
2
做一做:
(1)试举出互余、互补角的例子.
(2)30°与60°是互余的两角,能说30°是余角吗?
(3)∠1+∠2+∠3=90°,那么∠1、∠2、∠3互余,对吗?
(4)如果∠3+∠4=180°,那么∠3与∠4互余吗?
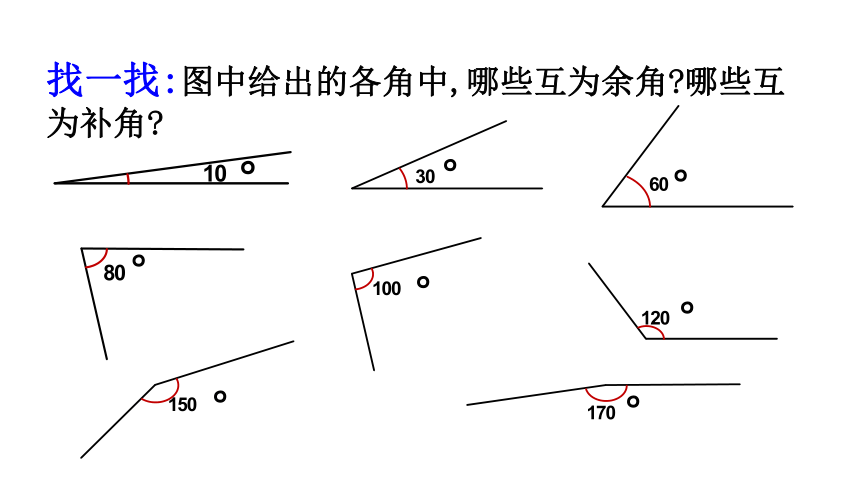
找一找:图中给出的各角中,哪些互为余角 哪些互为补角
°
°
°
°
°
°
°
°
填一填:
的锐角 的补角
85°
27°
140°
22°
34°25′
想一想:一个锐角的余角与它的补角有什么关系?
1.若∠α=20°,则∠α的余角=_______.
若∠β=20°,则∠β的余角=_______.
70°
70°
2.若∠α=50°,则∠α的余角=_______.
若∠β=50°,则∠β的余角=_______.
40°
40°
同角或等角的余角相等.
3.∠α的补角=180°-______ .
∠β的补角=_____- ∠β.
∠α
180°
同角或等角的补角相等.
例1:如图、已知∠AOC= ∠BOD=Rt ∠.指出图中还有哪些角相等, 并说明理由.
理由:
解:
∠COD +∠BOC=Rt ∠
∴ ∠AOB +∠BOC=Rt ∠
即∠AOB与 ∠COD都是∠BOC的余角
∠AOB=∠COD (同角的余角相等)
∠AOB= ∠COD
∵ ∠AOC= ∠BOD=Rt ∠
B
A
D
C
O
例2 已知一个角的补角是这个角的余角的4倍,
求这个角的度数.
解:设这个角为x度
根据题意180— x = 4(90—x)
解得 x=60(度)
求这个角的余角的度数.
方法1:直接求出:90°— 60°= 30°
方法2:设这个角的余角为x°,它的补角为(90+x)°
列出方程为: 90 + x = 4x
x = 30°
典例 · 精析区
以题说法 互动探究
练习1 如图,点O为直线AB上一点,∠BOC=Rt∠,OD是∠AOC内的一条射线,图中有哪几对角互余?哪几对角互补?
解:∵∠AOD+∠DOC=90°,
∴∠AOD与∠DOC互余.
∵∠AOD+∠DOB=180°,
∴∠AOD与∠DOB互补.
∵∠AOC+∠COB=180°,
∴∠AOC与∠COB互补.
随堂 · 检测区
即时演练 查漏补缺
练习2 如图,∠AOB、∠COD都是直角,请猜想∠AOD与∠COB在数量上是相等、
互余还是互补关系?请说明理由.
解:∠AOD与∠COB在数量上是互补关系.
∵∠AOD+∠COB=(∠AOB+∠BOD)+∠COB
=∠AOB+(∠BOD+∠COB)=90°+90°=180°,
∴∠AOD与∠COB互补.
典例 · 精析区
以题说法 互动探究
变式训练1 如图,O在直线AE上,CO平分∠AOE,∠DOB是直角.
(1)∠1的余角是______________,∠AOB的余角是______________,∠DOE的补角________.
(2)若∠COB=65°,求∠DOE的度数____________
∠DOE=65°
∠COB和∠DOE
∠BOC和∠DOE
∠AOD
学了这节课你有什么收获
谈一谈:
6.8余角和补角
问题1:有两堵围墙,有人想测地面上形成的∠AOB 的度数,但人又不能进入围墙,只能站在墙外,怎么测量呢?
延长BO到C(延长AO到D)
只要测出∠AOC 的度数,
即可求出∠AOB 的大小.
A
O
B
C
D
α
问题2:如图:一个破损的直角三角形,已知一个角为α,求另一个锐角的度数.
2
1
A
B
O
1、如果两个锐角的和是一个直角,那么这两个角互为余角,简称这两个角互余.其中一个角是另一个的余角.
几何语言
1
2、如果两个角的和是一个平角,那么这两个角互为补角,简称这两个角互补.其中一个角是另一个的补角.
A
B
O
几何语言
2
做一做:
(1)试举出互余、互补角的例子.
(2)30°与60°是互余的两角,能说30°是余角吗?
(3)∠1+∠2+∠3=90°,那么∠1、∠2、∠3互余,对吗?
(4)如果∠3+∠4=180°,那么∠3与∠4互余吗?
找一找:图中给出的各角中,哪些互为余角 哪些互为补角
°
°
°
°
°
°
°
°
填一填:
的锐角 的补角
85°
27°
140°
22°
34°25′
想一想:一个锐角的余角与它的补角有什么关系?
1.若∠α=20°,则∠α的余角=_______.
若∠β=20°,则∠β的余角=_______.
70°
70°
2.若∠α=50°,则∠α的余角=_______.
若∠β=50°,则∠β的余角=_______.
40°
40°
同角或等角的余角相等.
3.∠α的补角=180°-______ .
∠β的补角=_____- ∠β.
∠α
180°
同角或等角的补角相等.
例1:如图、已知∠AOC= ∠BOD=Rt ∠.指出图中还有哪些角相等, 并说明理由.
理由:
解:
∠COD +∠BOC=Rt ∠
∴ ∠AOB +∠BOC=Rt ∠
即∠AOB与 ∠COD都是∠BOC的余角
∠AOB=∠COD (同角的余角相等)
∠AOB= ∠COD
∵ ∠AOC= ∠BOD=Rt ∠
B
A
D
C
O
例2 已知一个角的补角是这个角的余角的4倍,
求这个角的度数.
解:设这个角为x度
根据题意180— x = 4(90—x)
解得 x=60(度)
求这个角的余角的度数.
方法1:直接求出:90°— 60°= 30°
方法2:设这个角的余角为x°,它的补角为(90+x)°
列出方程为: 90 + x = 4x
x = 30°
典例 · 精析区
以题说法 互动探究
练习1 如图,点O为直线AB上一点,∠BOC=Rt∠,OD是∠AOC内的一条射线,图中有哪几对角互余?哪几对角互补?
解:∵∠AOD+∠DOC=90°,
∴∠AOD与∠DOC互余.
∵∠AOD+∠DOB=180°,
∴∠AOD与∠DOB互补.
∵∠AOC+∠COB=180°,
∴∠AOC与∠COB互补.
随堂 · 检测区
即时演练 查漏补缺
练习2 如图,∠AOB、∠COD都是直角,请猜想∠AOD与∠COB在数量上是相等、
互余还是互补关系?请说明理由.
解:∠AOD与∠COB在数量上是互补关系.
∵∠AOD+∠COB=(∠AOB+∠BOD)+∠COB
=∠AOB+(∠BOD+∠COB)=90°+90°=180°,
∴∠AOD与∠COB互补.
典例 · 精析区
以题说法 互动探究
变式训练1 如图,O在直线AE上,CO平分∠AOE,∠DOB是直角.
(1)∠1的余角是______________,∠AOB的余角是______________,∠DOE的补角________.
(2)若∠COB=65°,求∠DOE的度数____________
∠DOE=65°
∠COB和∠DOE
∠BOC和∠DOE
∠AOD
学了这节课你有什么收获
谈一谈:
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
