7.5 一次函数的应用(2)[上学期]
文档属性
| 名称 | 7.5 一次函数的应用(2)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 793.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-06 22:15:00 | ||
图片预览


文档简介
课件15张PPT。7.5一次函数的应用(2)用一次函数解决实际问题的基本步骤是:
(1)先判断问题中的两个变量之间是不是一次函数关系。
(2)求得函数解析式。
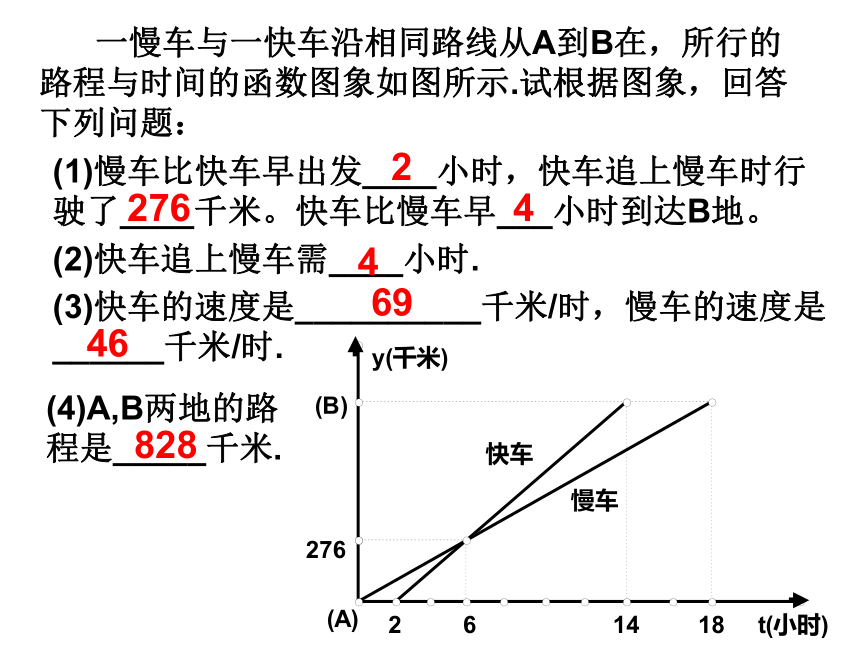
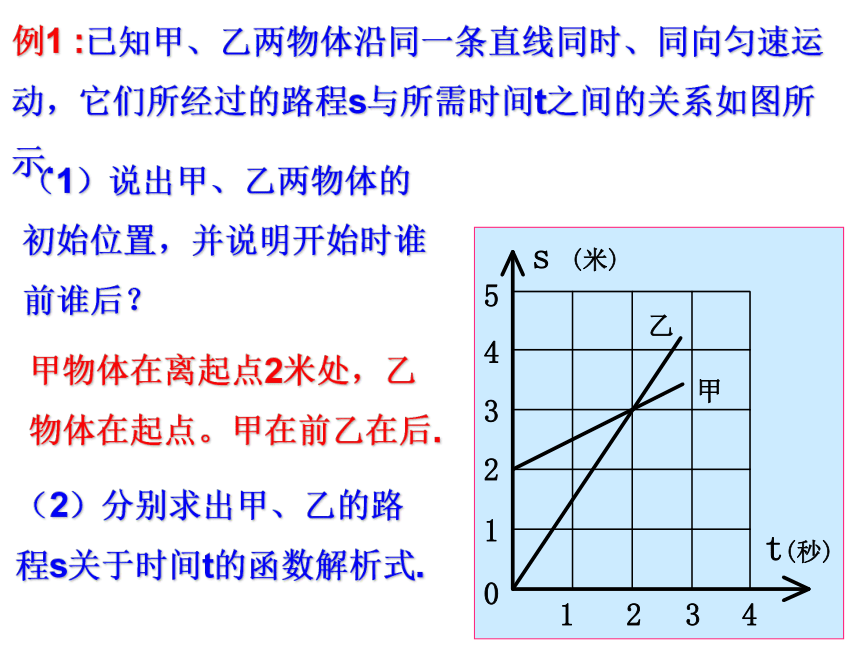
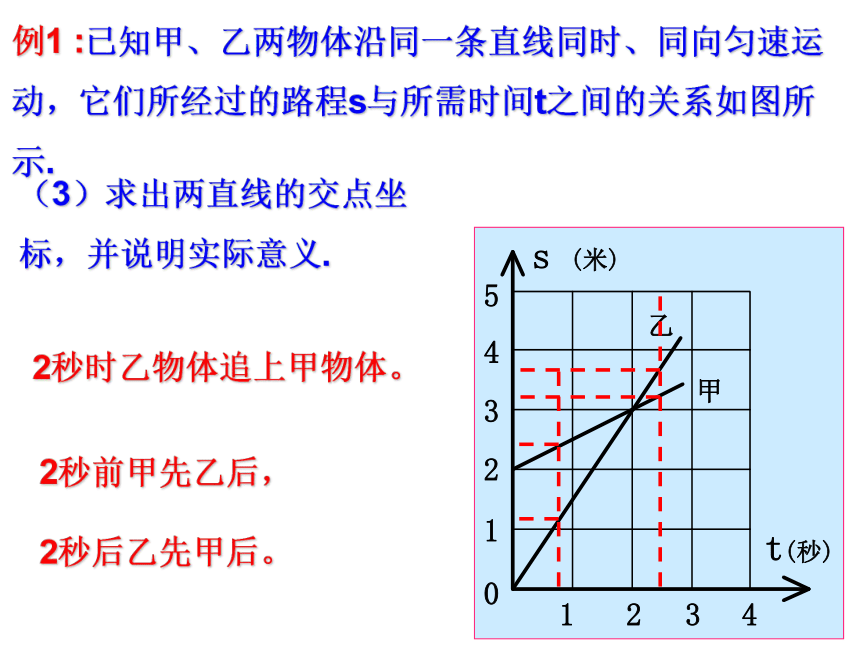
(3)利用函数解析式或其图象解决实际问题。 一慢车与一快车沿相同路线从A到B在,所行的路程与时间的函数图象如图所示.试根据图象,回答下列问题:(1)慢车比快车早出发____小时,快车追上慢车时行驶了____千米。快车比慢车早___小时到达B地。(2)快车追上慢车需____小时.(4)A,B两地的路程是_____千米.227644(3)快车的速度是__________千米/时,慢车的速度是______千米/时.6946828(1)说出甲、乙两物体的初始位置,并说明开始时谁前谁后?例1 :已知甲、乙两物体沿同一条直线同时、同向匀速运动,它们所经过的路程s与所需时间t之间的关系如图所示.(2)分别求出甲、乙的路程s关于时间t的函数解析式.甲物体在离起点2米处,乙物体在起点。甲在前乙在后.例1 :已知甲、乙两物体沿同一条直线同时、同向匀速运动,它们所经过的路程s与所需时间t之间的关系如图所示.(3)求出两直线的交点坐标,并说明实际意义.2秒时乙物体追上甲物体。2秒前甲先乙后,
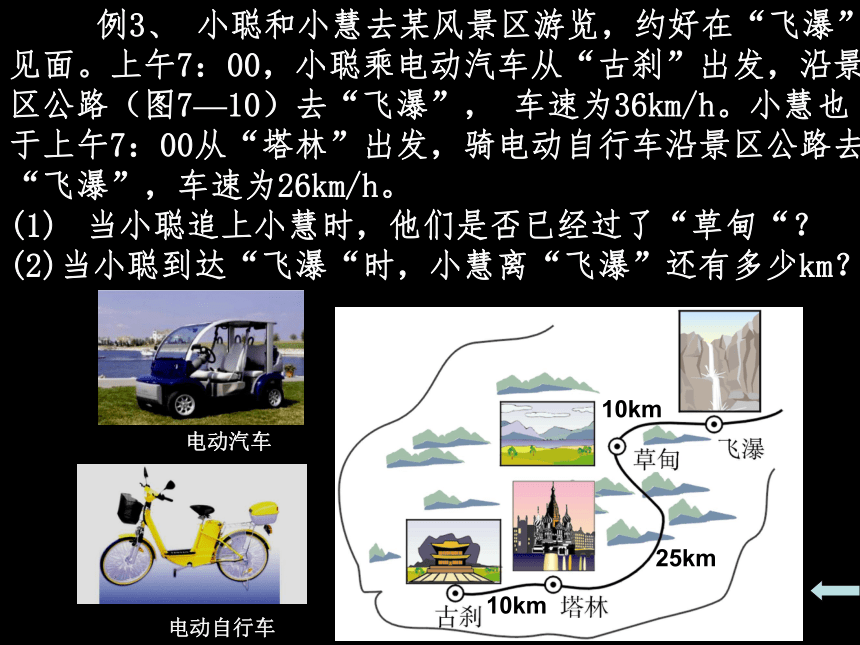
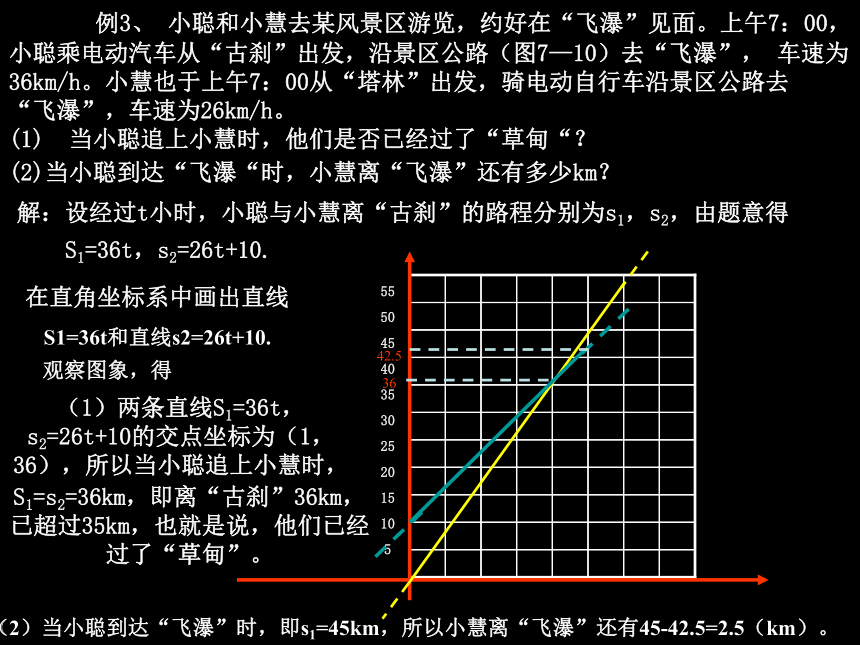
2秒后乙先甲后。 例3、 小聪和小慧去某风景区游览,约好在“飞瀑”
见面。上午7:00,小聪乘电动汽车从“古刹”出发,沿景
区公路(图7—10)去“飞瀑”, 车速为36km/h。小慧也
于上午7:00从“塔林”出发,骑电动自行车沿景区公路去
“飞瀑”,车速为26km/h。
(1)? 当小聪追上小慧时,他们是否已经过了“草甸“?
(2)当小聪到达“飞瀑“时,小慧离“飞瀑”还有多少km? 电动汽车电动自行车10km25km10km在直角坐标系中画出直线
S1=36t和直线s2=26t+10.解:设经过t小时,小聪与小慧离“古刹”的路程分别为s1,s2,由题意得S1=36t,s2=26t+10.观察图象,得0.25 0.5 0.75 1 1.25 1.5 1.75 2 55
50
45
40
35
30
25
20
15
10
53642.5(2)当小聪到达“飞瀑”时,即s1=45km,所以小慧离“飞瀑”还有45-42.5=2.5(km)。(1)两条直线S1=36t,s2=26t+10的交点坐标为(1,36),所以当小聪追上小慧时,S1=s2=36km,即离“古刹”36km,已超过35km,也就是说,他们已经过了“草甸”。 例3、 小聪和小慧去某风景区游览,约好在“飞瀑”见面。上午7:00,小聪乘电动汽车从“古刹”出发,沿景区公路(图7—10)去“飞瀑”, 车速为36km/h。小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去
“飞瀑”,车速为26km/h。
(1)? 当小聪追上小慧时,他们是否已经过了“草甸“?
(2)当小聪到达“飞瀑“时,小慧离“飞瀑”还有多少km? 达测深化做一做:
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。-6 -4 -22 4 6246-2-4-6利用一次函数的图象,求下列二元一次
方程组的解(或近似解):
(1) (2) 1,一次招聘会上,A,B两公司都在招聘销售人员。A公司给出的工资待遇是:每月1000元基本工资,另加销售额的2﹪作为奖金;B公司给出的工资待遇是:每月600元基本工资,另加销售额的4%作为奖金。如果你去应聘,那么你将怎样选择?探究活动: 2,某商场要印制商品宣传材料,甲印刷厂的
收费标准是:每份材料收1元印刷费,另收 1500元制版费;乙印刷厂的收费标准是:每份 材料收2.5元印制费,不收制版费。
(1)分别写出两厂的收费y(元)与印制数量x (份)之间的关系式;
(2)在同一直角坐标系中画出它们的图象。
(3)根据图象回答下列问题:
印制800份宣传材料时,选择哪一家印刷厂比较 合算?商场计划花费3000元用于印刷宣传材料,
找哪一家印刷厂能印刷宣传材料多一些?1.直角坐标系中两条直线(不平行于坐标轴)的交点坐标与两条直线的函数解析式所组成的二元一次方程组的解之间的关系。
2.会用一次函数的图象求二元一次
方程组的解(包括近似解)。今天的收获: 1,已知一次函数y=1.5x+m和y=-0.2x+n的图像都经过点A(4,3),则m=____,n=____.练习:2,函数y=2x+5,当x____时,函数值y=0,当x___时,函数值y>0,当x____时,函数值y<0.3,直线y=-2x+b,与x轴交于(-1,0),则不等式-2x+b<0的解集是______。4,已知关于x的函数ax+2=0的解为-6,则一次函数y=ax+2的图像不通过第___象限。5,托运行李x千克(x为整数)的费用为y元,已知托运一件行李的手续费为5元,每千克运费为1.2元,则y与x的关系式为__________。
(1)先判断问题中的两个变量之间是不是一次函数关系。
(2)求得函数解析式。
(3)利用函数解析式或其图象解决实际问题。 一慢车与一快车沿相同路线从A到B在,所行的路程与时间的函数图象如图所示.试根据图象,回答下列问题:(1)慢车比快车早出发____小时,快车追上慢车时行驶了____千米。快车比慢车早___小时到达B地。(2)快车追上慢车需____小时.(4)A,B两地的路程是_____千米.227644(3)快车的速度是__________千米/时,慢车的速度是______千米/时.6946828(1)说出甲、乙两物体的初始位置,并说明开始时谁前谁后?例1 :已知甲、乙两物体沿同一条直线同时、同向匀速运动,它们所经过的路程s与所需时间t之间的关系如图所示.(2)分别求出甲、乙的路程s关于时间t的函数解析式.甲物体在离起点2米处,乙物体在起点。甲在前乙在后.例1 :已知甲、乙两物体沿同一条直线同时、同向匀速运动,它们所经过的路程s与所需时间t之间的关系如图所示.(3)求出两直线的交点坐标,并说明实际意义.2秒时乙物体追上甲物体。2秒前甲先乙后,
2秒后乙先甲后。 例3、 小聪和小慧去某风景区游览,约好在“飞瀑”
见面。上午7:00,小聪乘电动汽车从“古刹”出发,沿景
区公路(图7—10)去“飞瀑”, 车速为36km/h。小慧也
于上午7:00从“塔林”出发,骑电动自行车沿景区公路去
“飞瀑”,车速为26km/h。
(1)? 当小聪追上小慧时,他们是否已经过了“草甸“?
(2)当小聪到达“飞瀑“时,小慧离“飞瀑”还有多少km? 电动汽车电动自行车10km25km10km在直角坐标系中画出直线
S1=36t和直线s2=26t+10.解:设经过t小时,小聪与小慧离“古刹”的路程分别为s1,s2,由题意得S1=36t,s2=26t+10.观察图象,得0.25 0.5 0.75 1 1.25 1.5 1.75 2 55
50
45
40
35
30
25
20
15
10
53642.5(2)当小聪到达“飞瀑”时,即s1=45km,所以小慧离“飞瀑”还有45-42.5=2.5(km)。(1)两条直线S1=36t,s2=26t+10的交点坐标为(1,36),所以当小聪追上小慧时,S1=s2=36km,即离“古刹”36km,已超过35km,也就是说,他们已经过了“草甸”。 例3、 小聪和小慧去某风景区游览,约好在“飞瀑”见面。上午7:00,小聪乘电动汽车从“古刹”出发,沿景区公路(图7—10)去“飞瀑”, 车速为36km/h。小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去
“飞瀑”,车速为26km/h。
(1)? 当小聪追上小慧时,他们是否已经过了“草甸“?
(2)当小聪到达“飞瀑“时,小慧离“飞瀑”还有多少km? 达测深化做一做:
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。-6 -4 -22 4 6246-2-4-6利用一次函数的图象,求下列二元一次
方程组的解(或近似解):
(1) (2) 1,一次招聘会上,A,B两公司都在招聘销售人员。A公司给出的工资待遇是:每月1000元基本工资,另加销售额的2﹪作为奖金;B公司给出的工资待遇是:每月600元基本工资,另加销售额的4%作为奖金。如果你去应聘,那么你将怎样选择?探究活动: 2,某商场要印制商品宣传材料,甲印刷厂的
收费标准是:每份材料收1元印刷费,另收 1500元制版费;乙印刷厂的收费标准是:每份 材料收2.5元印制费,不收制版费。
(1)分别写出两厂的收费y(元)与印制数量x (份)之间的关系式;
(2)在同一直角坐标系中画出它们的图象。
(3)根据图象回答下列问题:
印制800份宣传材料时,选择哪一家印刷厂比较 合算?商场计划花费3000元用于印刷宣传材料,
找哪一家印刷厂能印刷宣传材料多一些?1.直角坐标系中两条直线(不平行于坐标轴)的交点坐标与两条直线的函数解析式所组成的二元一次方程组的解之间的关系。
2.会用一次函数的图象求二元一次
方程组的解(包括近似解)。今天的收获: 1,已知一次函数y=1.5x+m和y=-0.2x+n的图像都经过点A(4,3),则m=____,n=____.练习:2,函数y=2x+5,当x____时,函数值y=0,当x___时,函数值y>0,当x____时,函数值y<0.3,直线y=-2x+b,与x轴交于(-1,0),则不等式-2x+b<0的解集是______。4,已知关于x的函数ax+2=0的解为-6,则一次函数y=ax+2的图像不通过第___象限。5,托运行李x千克(x为整数)的费用为y元,已知托运一件行李的手续费为5元,每千克运费为1.2元,则y与x的关系式为__________。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
