一次函数复习课[上学期]

课件18张PPT。制作人：平阳昆阳二中陈春莲一次函数复习课在一个过程中，可以取不同数值的量称为变 量： 在一个过程中，固定不变的量称为常 量：小王家离学校800米；小王步行速度100米/分钟时间（X）和小王离学校的距离（Y）一次函数复习　　1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。正比例函数是一次函数的特殊情况。kx ＋b≠０=０≠０kx★理解一次函数概念应注意下面两点：
⑴、解析式中自变量x的次数是___次，
⑵、比例系数_____。1K≠0 2、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的_________。
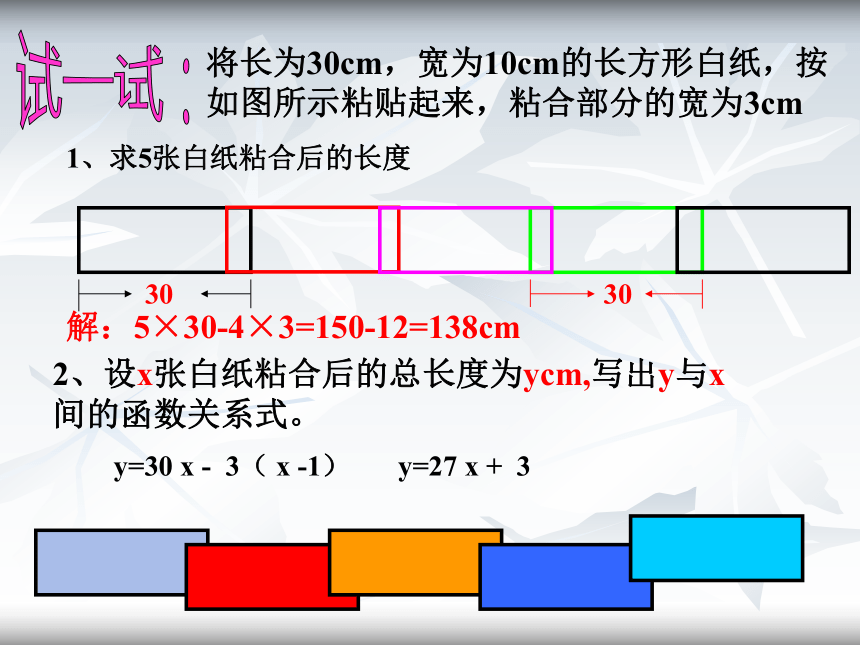
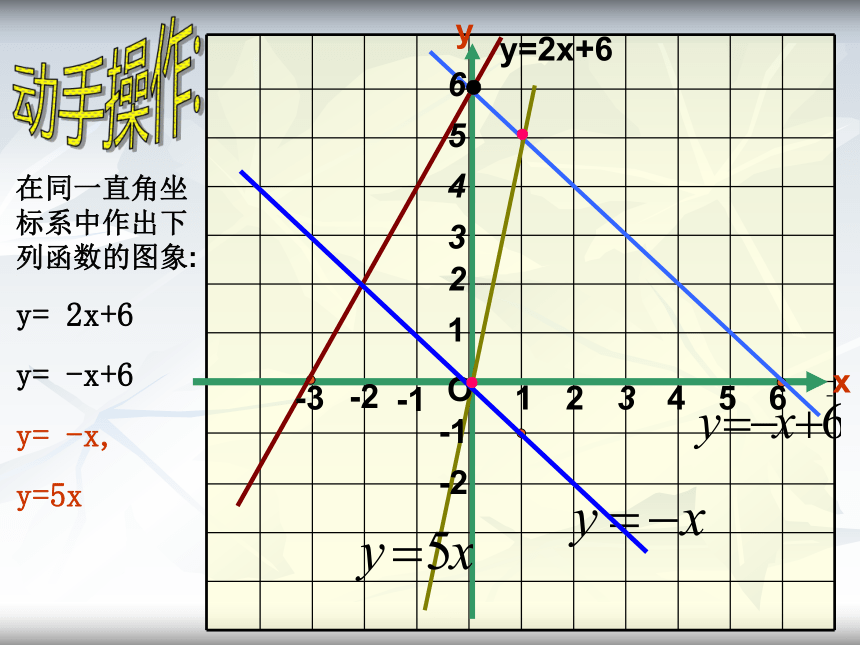
3、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。0，01，k 一条直线b一条直线一、知识要点：将长为30cm，宽为10cm的长方形白纸，按如图所示粘贴起来，粘合部分的宽为3cm1、求5张白纸粘合后的长度解：5×30-4×3=150-12=138cm2、设x张白纸粘合后的总长度为ycm,写出y与x间的函数关系式。试一试：y=30 x - 3（ x -1）y=27 x + 3在同一直角坐标系中作出下列函数的图象:
y= 2x+6
y= -x+6
y= -x,
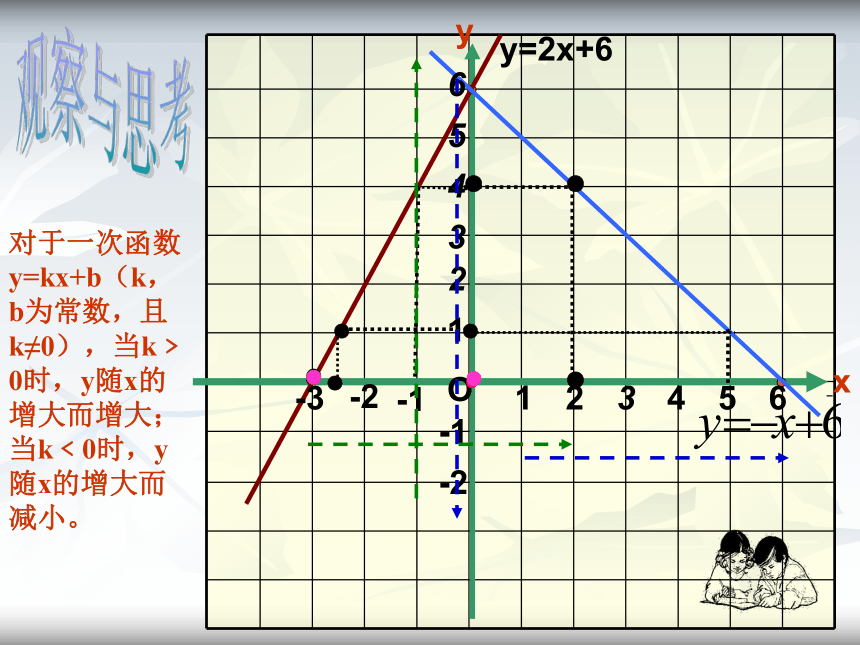
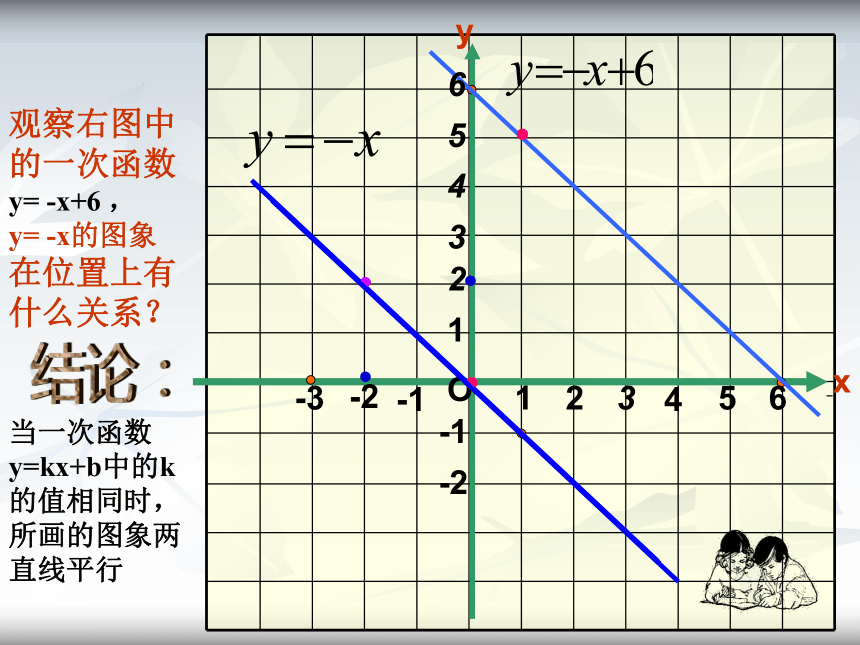
y=5xO21-1-121y=2x+6-23654354-3-26 xy●●动手操作:●O21-1-121y=2x+6-23654354-3-26 xy●观察与思考●●●●●●●●●对于一次函数y=kx+b（k，b为常数，且k≠0），当k﹥0时，y随x的增大而增大；当k﹤0时，y随x的增大而减小。O21-1-121-23654354-3-26 xy●●???观察右图中的一次函数y= -x+6 ，
y= -x的图象
在位置上有什么关系？结论：当一次函数y=kx+b中的k的值相同时，所画的图象两直线平行 1、在下列函数中， x是自变量， y是函数， 那些是一次函数？那些是正比例函数？
y=2x y=－3x+1 y=x22、某函数具有下列两条性质
（1）它的图像是经过原点（0，0）的一条直线；
（2）y的值随x值的增大而增大。
请你举出一个满足上述条件的函数（用关系式表示）3、函数 的图像与x轴交点坐标为________,
与y轴的交点坐标为____________。 ② 因为两个点（3，5）和（- 4，-9）都在函数图象上，所以都满足这个函数解析式，代入得：5=3k+b
-9=-4k+bk=2
b=-1例1：已知函数的图象过点（3，5）与（-4，-9），求这个一次函数的解析式。所以函数的解析式为：y=2x-1.解： ①设这个函数的解析式为 (1)先设出函数解析式用待定系数法求函数解析式步骤：（２）根据条件建立含k,b的两个方程（３）解方程组求出待定字母例2：某一次函数的图象与 x轴，y轴的交点分别是（4，0）和（0，-3），求出函数图象与两坐标轴构成的三角形的面积。解：如图所示：函数图象与坐标轴围成的三角形为△AOB●●OAB例３、已知y与x－1成正比例，x=8时，y=6，写出y与x之间函数关系式，并分别求出x=4和x=-3时y的值。解：∵ y与x－1成正比例 ∴y=k（x-1）
∵ 当x=8时，y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是：y= （x-1）当x=4时，y= ×（4－1）=当x=-3时，y= ×（-3－1）= 　　例4、　柴油机在工作时油箱中的余油量Q(千克）
与工作时间t（小时）成一次函数关系，当工作开始时
油箱中有油40千克，工作3.5小时后，油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式；（2）画出
这个函数的图象。解：（１）设Ｑ＝kt＋b。把t=0，Q=40；t=3.5，Q=22.5，分别代入上式，得解得解析式为：Q＝－５t+40　　(0≤t≤8)（２）、取t=0，得Q=40；取t=８，得Q=０。描出点
Ａ（０，40），B（8，0）。然后连成线段AB即是所
求的图形。注意：
（1）求出函数关系式时，必须找出自变量的取值范围。
（2）画函数图象时，应根据函数自变量的取值范围来确定图象的范围。图象是包括
两端点的线段..AB已知一次函数(1) k为何值时,它的图象经过原 点(2)k 为何值时,它的图象经过点(0, —2)(3)k 为何值时,它的图象平行直线 y=— x(4) k 为何值时, y随x的增大而减 小思维拓展 ２、已知函数 问当m为何值时，它是一次函数？１、在直角坐标系中，一次函数y＝kx＋b的图像经过三
点A（2，0）、B（0，2）、C（m，3），求这个函数
的关系式，并求m的值。延伸与提高小组合作交流　　　这节课你有何收获，
能与大家分享、交流你的感受吗？ 布置作业:见数学作业本中的复习题谢谢合作再见