函数、一次函数的应用[上学期]

课件27张PPT。1、函数的定义：
一般地，在某个变化过程中，有两个变量x和y，如果给定一个x值，相应地就确定另一个变量y的值，那么我们称y是x的函数，其中x是自变量，y是因变量。 2、函数图象的概念：
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它们的对应点，所有这些点组成的图形叫做该函数的图象。3、函数的表示方法
函数是研究现实世界变化规律的一个重要模型，函数的应用十分广泛，它的表示方式有三种，即图象法，表格法，代数表达式法，而且它们之间可以互相转化。2、一次函数，正比例函数的及联系
两个变量x、y间的关系式可以表示成 （ k≠0，k、b常数）的形式，则称称y是x的一次函数。
当b=0， 时，称y是x的正比例函数。4、一次函数 （ k≠0， k，b为常数）图象的特征与性质：
（1）一次函数的图象是过（0，b）、（ ，0）两点的一条直线；
（2）当k＞0时，y随x的增大而增大，k值越大，函数图象与x轴正方向所成的锐角越大；当k＜0时，y随x的增大而减小 正比例函数 图象的特征与性质：
1、正比例函数图象都是过原点（0，0）和（1，k）的一条直线；
2、当k＞0时，y随x的增大而增大，k值越大，函数图象与x轴正方向所成的锐角越大；当k＜0时，y随x的增大而减小。5、确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数，然后设其表达式为
或 。
②把已知点的坐标代入，若是正比例函数则需要一个点，若是一次函数，则需要二个点，组成关于k、b的一个或两个方程。
③解方程（组）得k、b的值。
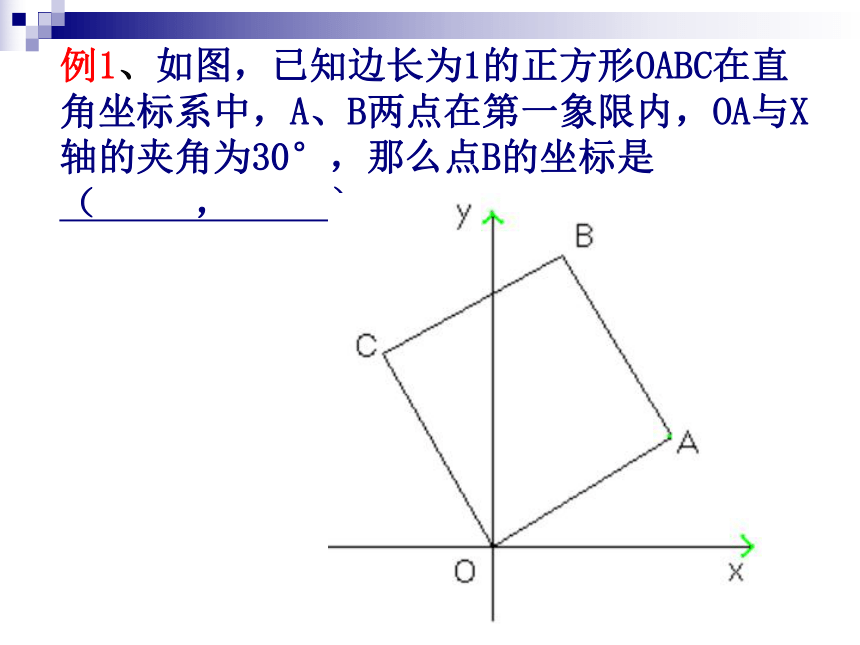
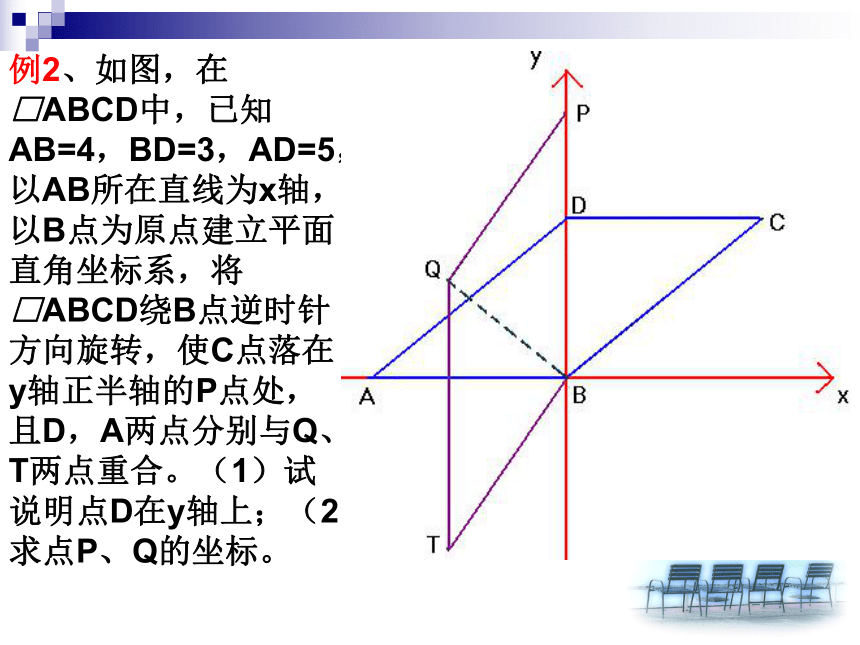
④把k、b代回代到表达式中，得到明朗化的解析式。例1、如图，已知边长为1的正方形OABC在直角坐标系中，A、B两点在第一象限内，OA与X轴的夹角为30°，那么点B的坐标是 （ ， ）。 例2、如图，在□ABCD中，已知AB=4，BD=3，AD=5，以AB所在直线为x轴，以B点为原点建立平面直角坐标系，将□ABCD绕B点逆时针方向旋转，使C点落在y轴正半轴的P点处，且D，A两点分别与Q、T两点重合。（1）试说明点D在y轴上；（2）求点P、Q的坐标。例3、如图，在矩形ABCD中，AB=4，BC=7，P是BC边上与B点不重合的动点，过点P的直线交CD的延长线于R，交AD于Q（Q与D不重合），且∠RPC=45o，设BP=x，梯形ABPQ的面积为y，求y与x之间的函数关系式，并求出自变量x的取值范围。 例4、某工厂加工一批产品,为了提前交货,规定每个工人完成100个以内,按每个产品2元付酬；超过100个，超过部分每个产品付酬增加0.2元；超过200个，超过部分除按以上规定外，每个产品付酬再增加0.3元，求每个工人：
（1）完成100个以内所得报酬y（元）与产品数x（个）之间的函数关系；
（2）完成100个以上但不超过200个，所得报酬y（元）与产品数x（个）之间的函数关系；
（3）完成200个以上所得报酬y（元）与产品数x（个）之间的函数关系。例7、某单位急需用车，但又不准备买车，他们准备和一个体车主或一国营出租车公司其中一家签订月租车合同，设汽车每月行驶x千米，应付给个体车主的月费用 元，应付给出租公司的月租费是 元， 、 分别与x之间的函数关系图象如上图所示，观察图象回答下列问题。
（1）每月行驶的路程在什么范围内时，租国营公司的车合算？
（2）每月行驶的路程等于多少时，租两家的费用相同？
（3）如果这个单位估计每月行驶的路程为2300千米，那么这个单位租哪一家的车合算？例11、观察甲、乙两图，解答下列问题
1、填空：两图中的 （ ）图比较符合传统寓言故事《龟免赛跑》中所描述的情节。3、根据1中所填答案的图象求：
（1）龟免赛跑过程中的函数关系式（要注明各函数的自变量的取值范围）；
（2）乌龟经过多长时间追上了免子，追及地距起点有多远的路程？4、请你根据另一幅图表，充分发挥你的想象，自编一则新的“龟免赛跑”的寓言故事，要求如下：
（1）用简洁明快的语言概括大意，不能超过200字；
（2）图表中能确定的数值，在故事叙述中不得少于3个，且要分别涉及时间、路和速度这三个量。 例12、如图，△ABC为正三角形，点B的坐标为（2，0），过C（-2，0）作直线L交OA于点D，交AB于点E，且使△ADE和△DCO的面积相等，求直线L的函数表达式。例13、（2002年湖北荆州市中考试题）一报刊销售亭从报社订购某晚报的价格是每份0.7元，销售价是每份1元，卖不掉的报纸还可以0.2元的价格退回报社。在一个月内（按30天计算），有20天每天卖出100份，其余10天每天只能卖出60份，但每天报亭从报社订购的份数必须相同。若以报亭每天从报社订购的份数为自变量x，每月所获得的利润y为函数。
（1）写出x与y之间的函数关系式，并指出自变量x的取值范围；
（2）报亭应该每天从报社订购多少份报纸，才能使每月获得的利润最大？最大利润是多少？例14、A市和B市分别有某种库存机器12台和6台，现决定支援C村10台，D村8台，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，从B市调运一台机器到C村和D村的运费分别是300元和500元．
(1)设B市运往C村机器x台，求总运费W关于x的函数关系式；
(2)若要求总运费不超过9000元，共有几种调运方案？
(3)求出总运费最低的调运方案，最低运费是多少元？例15（2003年江苏镇江市中考试题）在举国上下众志成诚，共同抗击非典的非常时期，英雄模范医药器械厂接受了生产一批高质量医用口罩的任务。要求在8天之内（含8天）生产A型和B型两种型号的口罩共5万只，其中A型口罩不得少于是1.8万只，该厂的生产能力是：若生产A型口罩，每天能生产0.6万只；若生产B型口罩，每天能生产0.8万只。已知生产一只A型口罩可获利0.5元，生产一只B型口罩可获利0.3元。
设该厂在此次任务中生产了A型口罩x万只。问：
（1）该厂生产A型口罩可获利润 万元，生产B型口罩可获利润 万元；
（2）设该厂这次生产口罩的总利润是y万元。试写出y关于x的函数关系式，并求出自变量x的取值范围；
（3）如果你是该厂厂长：
①在完成任务的前提下，你如何安排生产A型和B型口罩的只数，使获得的总利润最大？最大利润是多少？
②若要在最短时间内完成任务，你又如何来安排生产A型和B型口罩的只数？最短时间是多少？好好学习，天天向上