7.5一次函数的应用(2)[上学期]

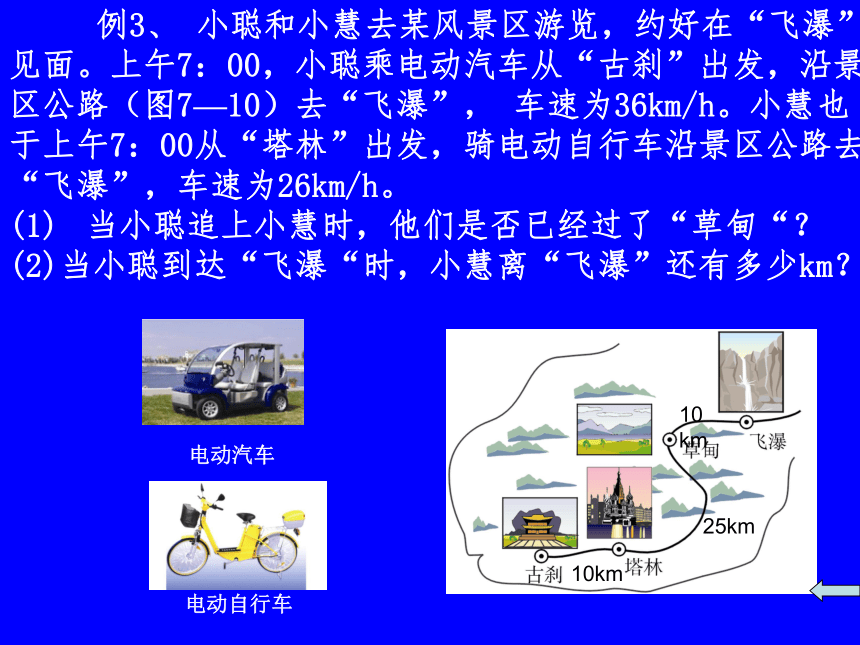
课件13张PPT。7.5一次函数的应用（2） 在运用一次函数解决实际问题时，首先判定问题中的两个变量之间是不是一次函数，当确定是一次函数时，可求出解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果。回顾 例3、 小聪和小慧去某风景区游览，约好在“飞瀑”
见面。上午7：00，小聪乘电动汽车从“古刹”出发，沿景
区公路（图7—10）去“飞瀑”， 车速为36km/h。小慧也
于上午7：00从“塔林”出发，骑电动自行车沿景区公路去
“飞瀑”，车速为26km/h。
(1)? 当小聪追上小慧时，他们是否已经过了“草甸“？
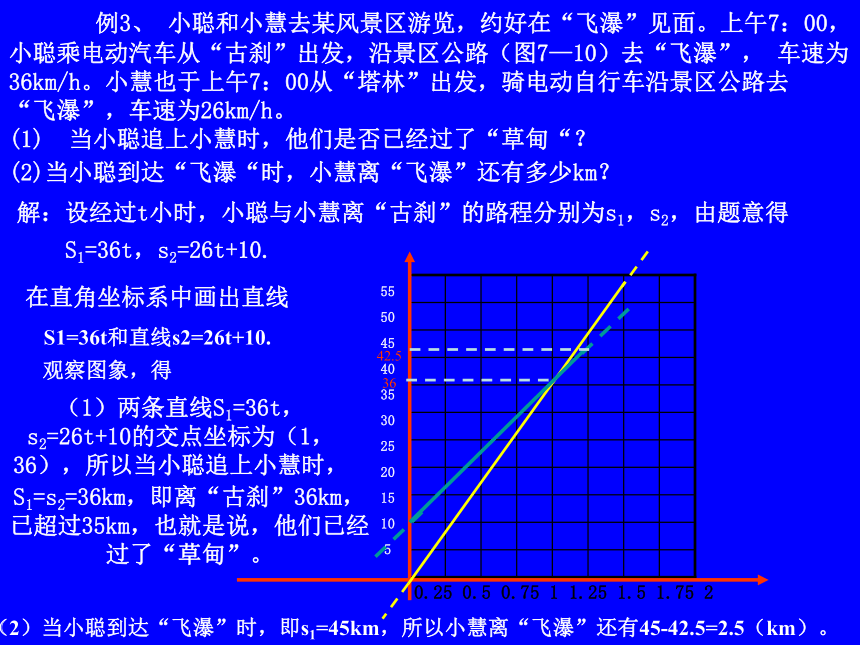
(2)当小聪到达“飞瀑“时，小慧离“飞瀑”还有多少km？ 电动汽车电动自行车10km25km10km10km25km10km在直角坐标系中画出直线
S1=36t和直线s2=26t+10.解：设经过t小时，小聪与小慧离“古刹”的路程分别为s1，s2，由题意得S1=36t，s2=26t+10.观察图象，得0.25 0.5 0.75 1 1.25 1.5 1.75 2 55
50
45
40
35
30
25
20
15
10
53642.5（2）当小聪到达“飞瀑”时，即s1=45km，所以小慧离“飞瀑”还有45-42.5=2.5（km）。（1）两条直线S1=36t，s2=26t+10的交点坐标为（1，36），所以当小聪追上小慧时，S1=s2=36km，即离“古刹”36km，已超过35km，也就是说，他们已经过了“草甸”。 例3、 小聪和小慧去某风景区游览，约好在“飞瀑”见面。上午7：00，小聪乘电动汽车从“古刹”出发，沿景区公路（图7—10）去“飞瀑”， 车速为36km/h。小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去
“飞瀑”，车速为26km/h。
(1)? 当小聪追上小慧时，他们是否已经过了“草甸“？
(2)当小聪到达“飞瀑“时，小慧离“飞瀑”还有多少km？ 达测深化做一做：
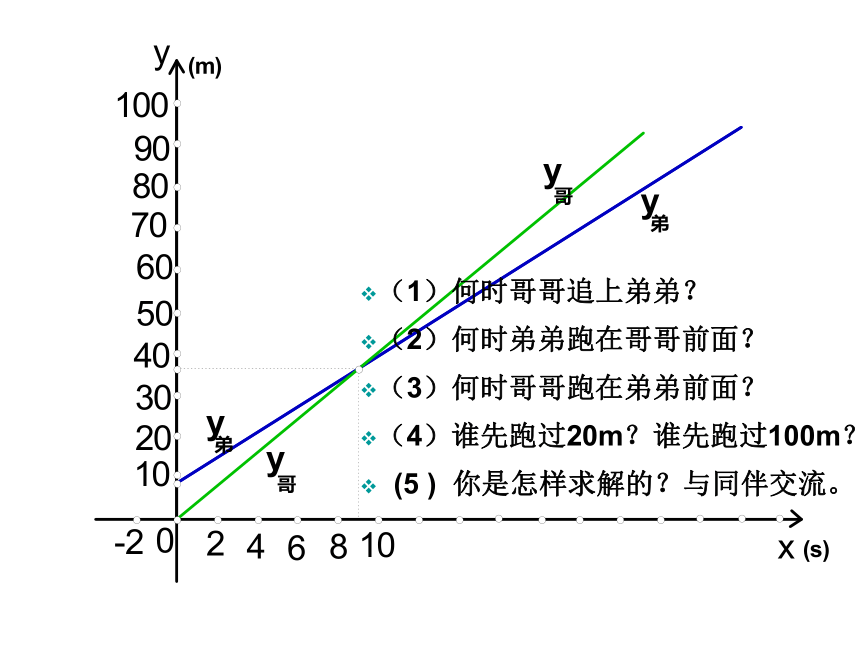
兄弟俩赛跑，哥哥先让弟弟跑9m，然后自己才开始跑。已知弟弟每秒跑3m，哥哥每秒跑4m。列出函数关系式，作出函数图象，观察图象回答下列问题：
（1）何时哥哥追上弟弟？
（2）何时弟弟跑在哥哥前面？
（3）何时哥哥跑在弟弟前面？
（4）谁先跑过20m？谁先跑过100m？
(5 ) 你是怎样求解的？与同伴交流。（1）何时哥哥追上弟弟？
（2）何时弟弟跑在哥哥前面？
（3）何时哥哥跑在弟弟前面？
（4）谁先跑过20m？谁先跑过100m？
(5 ) 你是怎样求解的？与同伴交流。　　我边防局接到情报，近海处有一可疑船只A正向公海方向行驶。边防局迅速派出快艇B追赶（如下图），海
岸公
海AB探究学习下图中l1 ，l2分别表示两船相对于海岸的距离s（海里）
与追赶时间t（分）之间的关系。根据图象回答下列问题：（1）哪条线表示B到海岸的距离与追赶时间之间的关系？解：观察图象，得当t＝0时，B距海岸0海里，即
　　　　　　　　　　　　　　　　S＝0，故l1表
　　　　　　　　　　　　　　　　示B到海岸的距
　　　　　　　　　　　　　　　　离与追赶时间之
　　　　　　　　　　　　　　　　间的关系；（2）A、B哪个速度快？从0增加到10时， l2的纵坐标增加了2，而l1的纵坐标增加了5，即10分内，A行驶了2海里，B行驶了5海里，所以B的速度快。（3）15分内B能否追上A？l1l2延长l1，l2，　　　　　可以看出，当t＝15时，l1上对应点在l2
上对应点的下方，这表明，15分时B尚未追上A。　　如图l1 ，l2相交于点P。（4）如果一直追下去，那么B能否追上A？l1l2因此，如果一直追下去，那么B一定能追上A。P（5）当A逃到离海岸12海里的公海时，B将无法对其进行检查。照此速度，B能否在A逃入公海前将其拦截？l1l2P　　从图中可以看出，l1与l1交点P的纵坐标小于12，　想一想你能用其他方法解决
上述问题吗？这说明在A逃入公海前，我边防快艇B能够追上A。再见