7.4一次函数图象（2）[上学期]

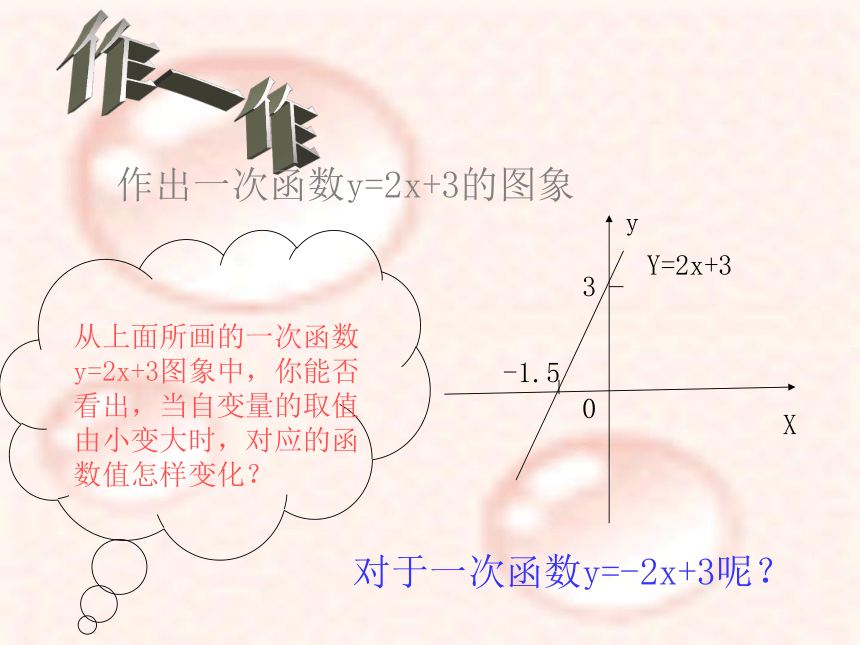
课件18张PPT。7.4一次函数图象（2）郑楼中学 杨焕勇郑楼中学 杨焕勇　　一次函数y=kx+b的图象是一条直线。作一次函数图象时，只要确定两个点，再过这两个点作直线就可以了。忆一忆还记得一次函数的图象是?如何画一次函数的图象?作一作作出一次函数y=2x+3的图象X y03-1.5Y=2x+3对于一次函数y=-2x+3呢？121-1-2y=-2x+3y=2x+3发现:
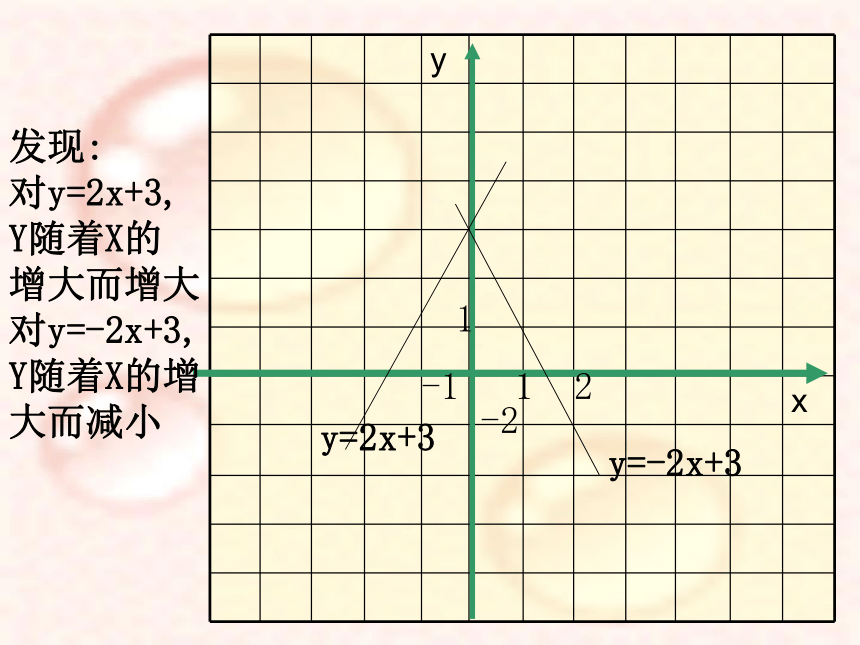
对y=2x+3,
Y随着X的
增大而增大
对y=-2x+3,
Y随着X的增
大而减小
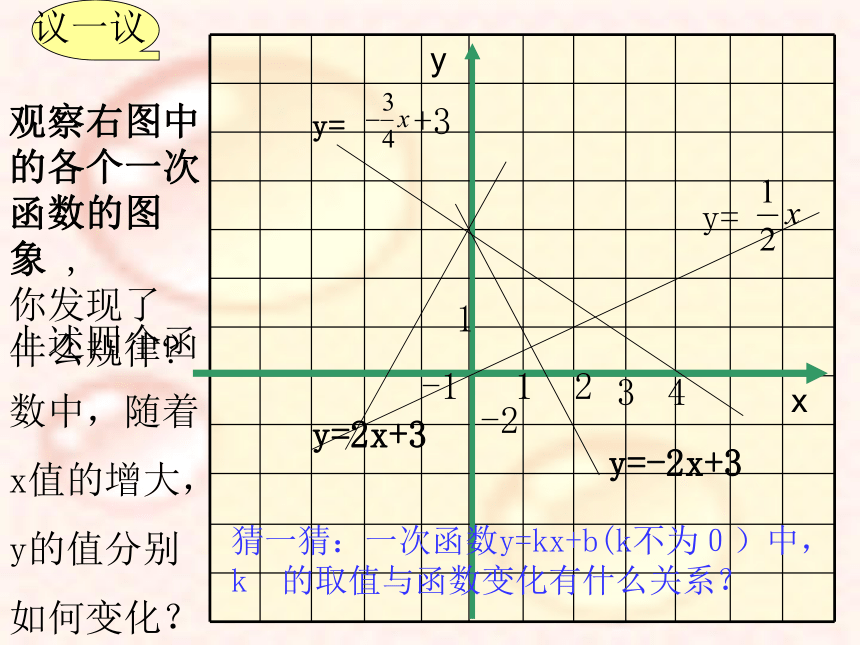
121-1-2y=-2x+3y=2x+3y=+334y=议一议观察右图中
的各个一次
函数的图象 ,
你发现了
什么规律?上述四个函
数中，随着
x值的增大，
y的值分别
如何变化？猜一猜：一次函数y=kx+b(k不为０）中，k 的取值与函数变化有什么关系？一次函数的性质在一次函数y=kx+b中，
当k﹥0时，y的值随x的值的增大而增大；
当k﹤0时，y的值随x的值的增大而减小。学 以 致 用下列函数,y的值随着x值的增大如何变化？做一做:
第170 页例2、我国某地区现有人工造林面积12万公顷，规划今后10年新造林61000～62000公顷。请估计6年后该地区的造林总面积达到多少？试一试解：设P表示今后10年平均造林的公顷数，
则61000≤P≤6200.设6年后该地区的造林
总面积达到S公顷，则S=6P+120000在这个一次函数中，一次项系数K=6＞0，
所以S随着P的增大而增大。∵ 61000≤P≤6200，∴6×6100+12000≤S≤6×6200+120000即15600≤S≤157200答：6年后该地区的造林总面积达到15.66万～15.72万公顷。你行吗？例3要从甲、乙两仓库向A、B两工地运送水泥。已知
甲仓库可运出水泥100吨，乙仓库可运出80吨；A工地
需70吨水泥，B工地需110吨水泥。两仓库到A，B两
工地的路程和每吨千米的运费如下表：（1）设甲仓库运往A地水泥x吨，求总运费y
关于x的函数解析式．
（２）当甲、乙两仓库运往Ａ，Ｂ工地多少
水泥时，总运费最省？解：各仓库运出的水泥吨数和运费如下表：∴y=1.2×20x+1×25(100-x)+1.2×15 (70-x)
+0.8×20(10+x)
=-3x+3920 (0≤x≤70)４０６０８０（吨）（元）３７００３８００３９００３７１０３９２０函数：
y= -3x+3920
(0≤x≤70)
的图象如右图所示．
说明：右图的纵轴中３７００以下的刻度省略．（２）解：在一次函数y= -3x+3920 中，
Ｋ＝－３＜０，所以的值随X的增大而
减小．因为0≤x≤70，所以当x=70时，
y的值最小．当x=70时，由表格可知，当甲仓库向Ａ，Ｂ
两工地各运送７０吨和３０吨，乙仓库不向
Ａ工地运送水泥，而只向Ｂ工地运讼８０吨时，
总运费最省．最省运费为：
－３×７０＋３９２０＝３７１０（元）挑 战 自 己1、y=x+1与坐标轴的交点坐标？
2、y=(-3 k+1) x+2 k-1的图象
经过原点，确定k的值？3、写出m的3个值，使相应的一次
函数y=(2m-1)x+2的值都是随着x值
的增大而减小. 4、一次函数y=kx+b的图象如图所示，则
k 0,b 0 挑 战 自 己xyo<<小 结你说，我说，大家一起说！通过本节课的学习，你掌握了哪些知识？一次函数的图象和性质小结：过(0,b)的直线
过(0,0)的直线
k＞0
k＜0y随x的增大而增大
y随x的增大而减小