期末专题复习一次函数[上学期]

期末专题复习 一次函数
【知识导航】
1. 正比例函数和一次函数的概念及函数的三种表示方法
2. 用待定系数法求一次函数的解析式
3. 一次函数图像的意义
【例题解析】
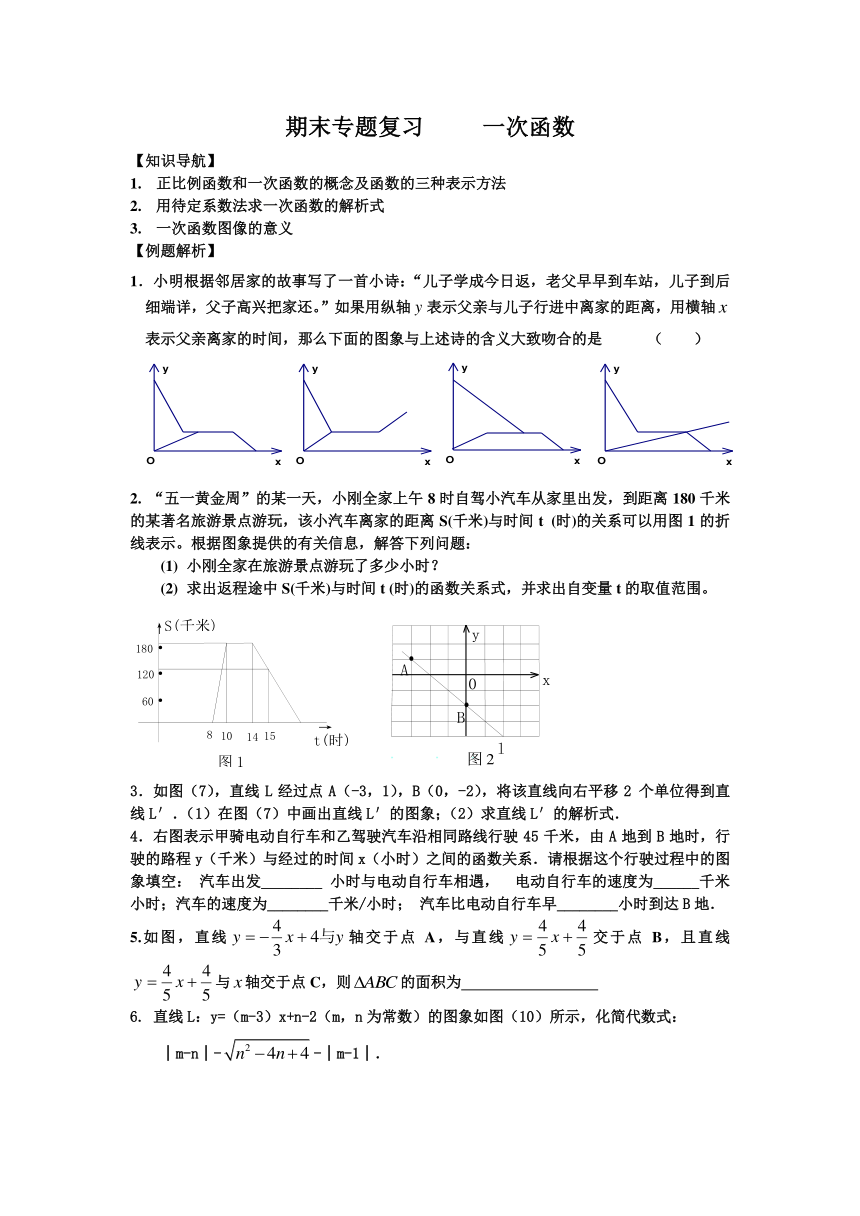
1．小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还。”如果用纵轴表示父亲与儿子行进中离家的距离，用横轴表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是 （ ）
2. “五一黄金周”的某一天，小刚全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩，该小汽车离家的距离S(千米)与时间t (时)的关系可以用图1的折线表示。根据图象提供的有关信息，解答下列问题：
(1) 小刚全家在旅游景点游玩了多少小时？
(2) 求出返程途中S(千米)与时间t (时)的函数关系式，并求出自变量t的取值范围。
HYPERLINK "http://"
EMBED Word.Picture.8
3．如图（7），直线L经过点A（-3，1），B（0，-2），将该直线向右平移2个单位得到直线L′．（1）在图（7）中画出直线L′的图象；（2）求直线L′的解析式．
4．右图表示甲骑电动自行车和乙驾驶汽车沿相同路线行驶45千米，由A地到B地时，行驶的路程y（千米）与经过的时间x（小时）之间的函数关系．请根据这个行驶过程中的图象填空：汽车出发________小时与电动自行车相遇，电动自行车的速度为______千米小时；汽车的速度为________千米/小时；汽车比电动自行车早________小时到达B地．
5.如图，直线轴交于点A，与直线交于点B，且直线与轴交于点C，则的面积为　　　　　　　　　
6. 直线L：y=（m-3）x+n-2（m，n为常数）的图象如图（10）所示，化简代数式：
│m-n│--│m-1│．
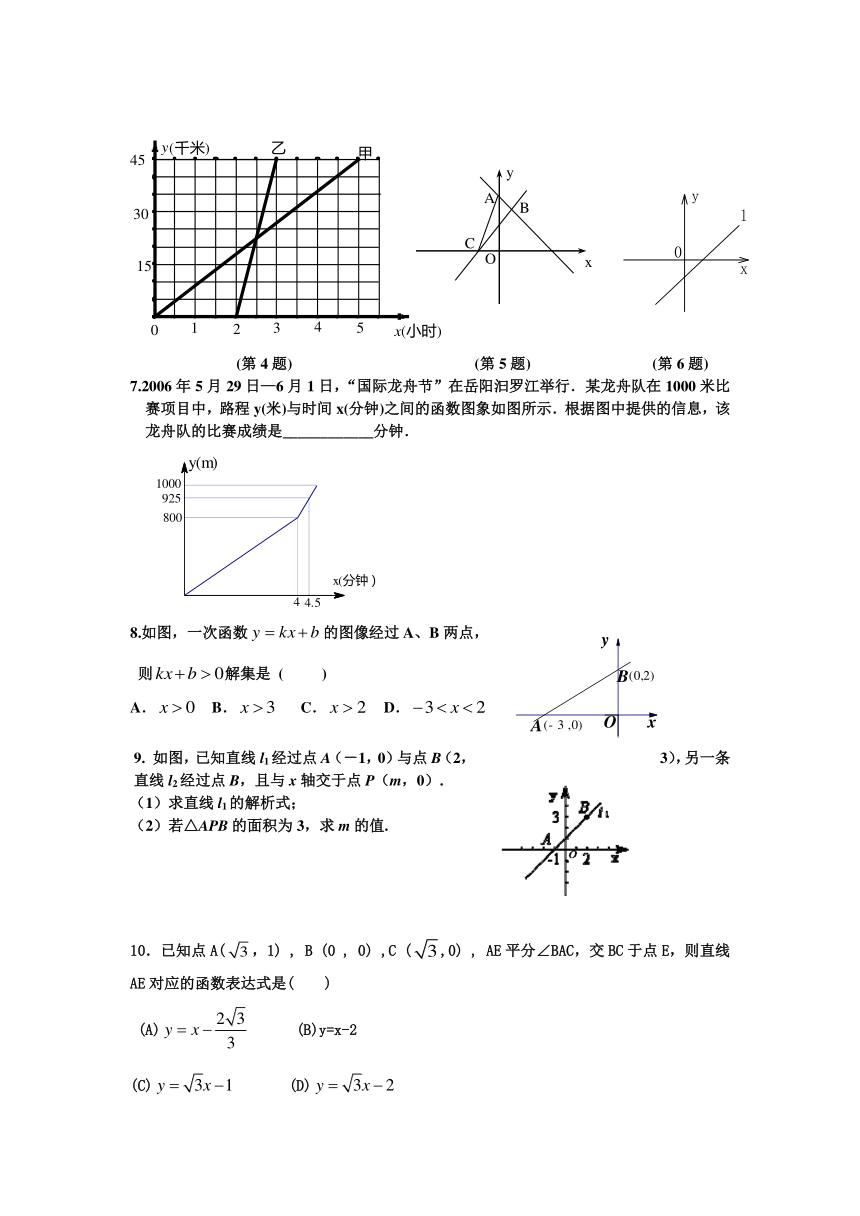
(第4题) (第5题) (第6题)
7.2006年5月29日—6月1日，“国际龙舟节”在岳阳汩罗江举行．某龙舟队在1000米比赛项目中，路程y(米)与时间x(分钟)之间的函数图象如图所示．根据图中提供的信息，该龙舟队的比赛成绩是____________分钟．
8.如图，一次函数的图像经过A、B两点，
则解集是 ( )
A． B． C． D．
9. 如图，已知直线l1经过点A（－1，0）与点B（2，3），另一条直线l2经过点B，且与x轴交于点P（m，0）.
（1）求直线l1的解析式；
（2）若△APB的面积为3，求m的值.
10．已知点A(，1) , B (0 , 0) ,C (,0) , AE平分∠BAC，交BC于点E，则直线AE对应的函数表达式是( )
(A) HYPERLINK "http://" EMBED Equation.DSMT4 (B)y=x-2
(C) (D)
【习题精选】
1．小亮早晨从家骑车到学校，先上坡后下坡，行程情况如图所示．若返回时上坡、下坡的速度仍保持不变，那么小明从学校骑车回家用的时间是( )
(A) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟
2、已知直线y＝ax＋b (a≠0)如图5所示，则|a＋b|－(a－b)＝ .
3．（本小题12分）为了鼓励小强勤做家务，培养他的劳动意识，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的。若设小强每月的家务劳动时间为x小时，该月可得（即下月他可获得）的总费为y元，则y（元）和x（小时）之间的函数图像如图所示。
（1） 根据图像，请你写出小强每月的基本生活费为多少元；
（2） 父母是如何奖励小强家务劳动的？
（2）写出当0≤x≤20时，相对应的y与x之间的函数关系式；
（3）若小强5月份希望有250元费用，则小强4月份需做家务多少时间？
4.如图，在平面直角坐标系中，点A在第一象限，点B的坐标为（3，0），OA=2，∠AOB=60°
(I) 求点A的坐标：
(2)若直线AB交x轴于点C，求△AOC的面积.
5.某块试验田里的农作物每天的需水量(千克)与生长时间(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克，在第40天后每天的需水量比前一天增加100千克.
(1)分别求出≤40和≥40时与之间的关系式；
(2)如果这些农作物每天的需水量大于或等于4000千克时
需要进行人工灌溉，那么应从第几天开始进行人工灌溉？
6．已知：如图1，点G是BC的中点，点H在AF上，动点P以每秒2的速度沿图1的边线运动，运动路径为：，相应的△ABP的面积关于运动时间的函数图像如图2，若，则下列四个结论中正确的个数有
①图1中的BC长是8; ②图2中的M点表示第4秒时的值为24;
③图1中的CD长是4; ④图2中的N点表示第12秒时的值为18.
7.如图，直角坐标系中，点A的坐标为（1，0），以线段
OA为边在第四象限内作等边△AOB，点C为x正半轴上
一动点(OC＞1)，连结BC，以线段BC为边在第四象限内
作等边△CBD，直线DA交y轴于点E.
（1）△OBC与△ABD全等吗？判断并证明你的结论;
（3） 随着点C位置的变化，点E的位置是否会发生变化
（4） 若没有变化，求出点E的坐标；若有变化，请说明理由.
y
O
x
A
B
C
第7题图
y
x