1.2有关三角函数的计算(2)[下学期]
文档属性
| 名称 | 1.2有关三角函数的计算(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 307.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-17 20:28:00 | ||
图片预览




文档简介
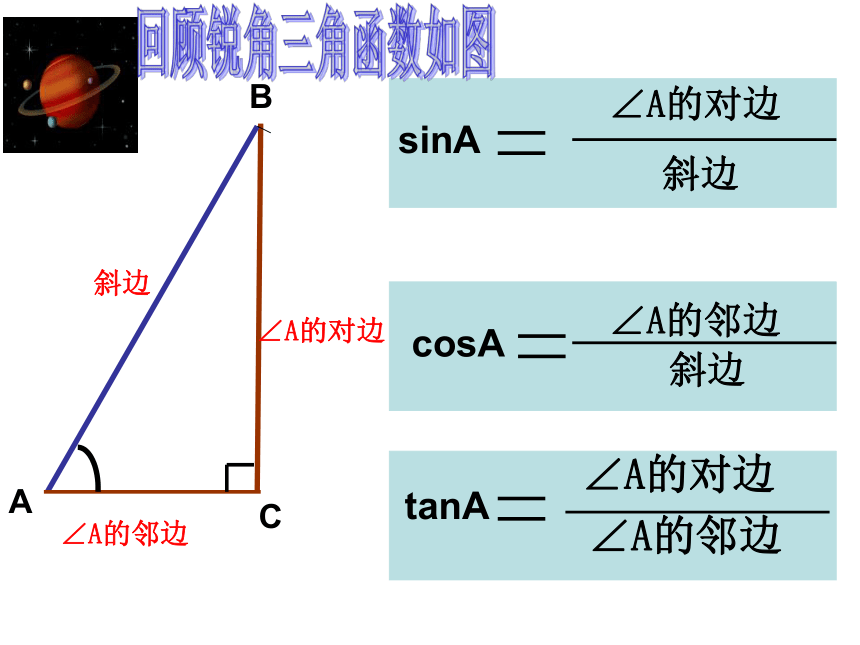
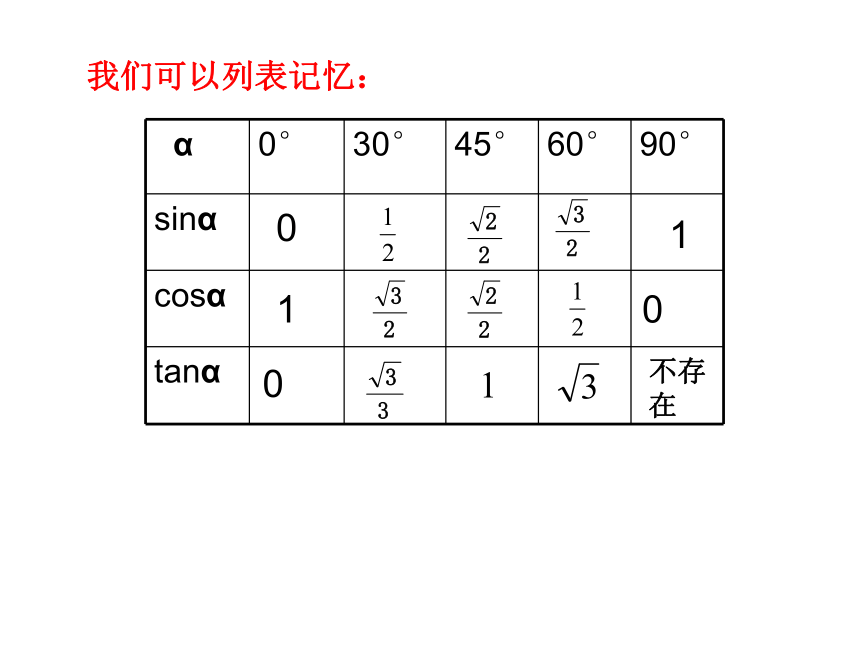
课件12张PPT。1.2有关三角函数的计算(2)课件制作人:昆二中陈春莲 AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边回顾锐角三角函数如图互余两角之间的三角函数关:
sinA=cosB,tanA.tanB=1.同角之间的三角函数关系:
sin2A+cos2A=1.tanA=特殊角300,450,600角的三角函数值.我们可以列表记忆:01100不存在锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围1. 当 锐角A>45°时,sinA的值( )(A)小于 (B)大于
(C) 小于 (D)大于B(A)小于 (B)大于
(C) 小于 (D)大于2. 当锐角A>30°时,cosA的值( )C上一页下一页锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°3. 当∠A为锐角,且tanA的值大于 时,∠A( )B4. 确定角的范围4. 当∠A为锐角,且tanA的值小于 时,∠A( )(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°C锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围5.当∠A为锐角,且cosA=
那么( )4. 确定角的范围(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° 6. 当∠A为锐角,且sinA=
那么( )(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° DASHIFT20917.301507834sin·7=已知三角函数值求角度,要用到sin,Cos,tan的第二功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:如果再按“度分秒健”就换算成度分秒,°′″即∠ α=17018’5.43”2ndf2094sin·7已知三角函数值求角度,要用到sin,Cos,tan的第二功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:即∠ α=17018’5.43”2ndfDMS例如,根据下面的条件,求锐角β的大小(精确到1”
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036
按键盘顺序如下:26048’51”0.sin115=4DMSSHIFT°′″2ndfsin0.45112ndf26048’51”即∠ β =26048’51”例2、一段公路弯道呈弧形,测得弯道
AB两端的距离为200米,AB 的半径为1000米,求弯道的长(精确到0.1米)⌒⌒ABOR谈谈今天的收获畅所欲言
sinA=cosB,tanA.tanB=1.同角之间的三角函数关系:
sin2A+cos2A=1.tanA=特殊角300,450,600角的三角函数值.我们可以列表记忆:01100不存在锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围1. 当 锐角A>45°时,sinA的值( )(A)小于 (B)大于
(C) 小于 (D)大于B(A)小于 (B)大于
(C) 小于 (D)大于2. 当锐角A>30°时,cosA的值( )C上一页下一页锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°3. 当∠A为锐角,且tanA的值大于 时,∠A( )B4. 确定角的范围4. 当∠A为锐角,且tanA的值小于 时,∠A( )(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°C锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围5.当∠A为锐角,且cosA=
那么( )4. 确定角的范围(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° 6. 当∠A为锐角,且sinA=
那么( )(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° DASHIFT20917.301507834sin·7=已知三角函数值求角度,要用到sin,Cos,tan的第二功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:如果再按“度分秒健”就换算成度分秒,°′″即∠ α=17018’5.43”2ndf2094sin·7已知三角函数值求角度,要用到sin,Cos,tan的第二功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:即∠ α=17018’5.43”2ndfDMS例如,根据下面的条件,求锐角β的大小(精确到1”
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036
按键盘顺序如下:26048’51”0.sin115=4DMSSHIFT°′″2ndfsin0.45112ndf26048’51”即∠ β =26048’51”例2、一段公路弯道呈弧形,测得弯道
AB两端的距离为200米,AB 的半径为1000米,求弯道的长(精确到0.1米)⌒⌒ABOR谈谈今天的收获畅所欲言
