5.6三角形的中位线[下学期]

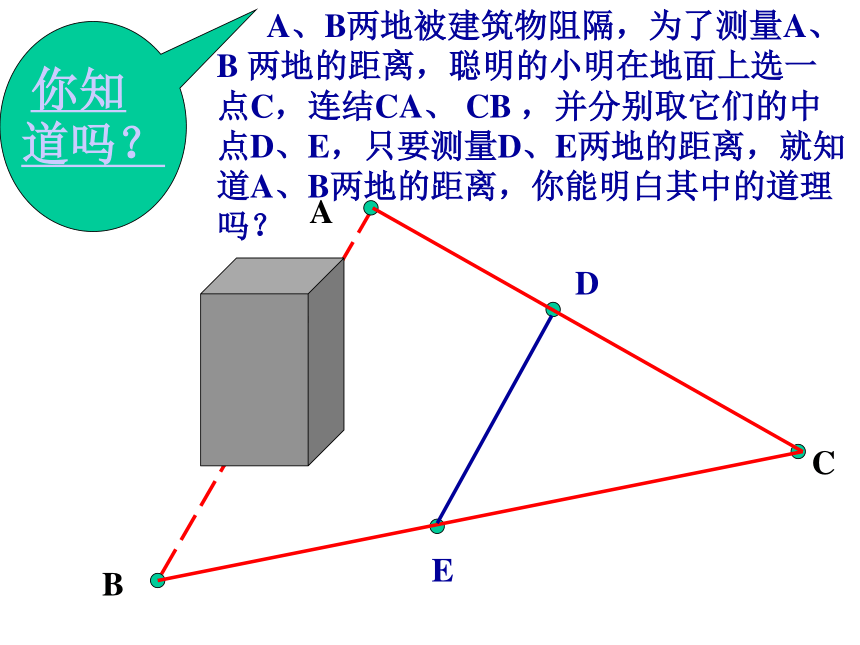
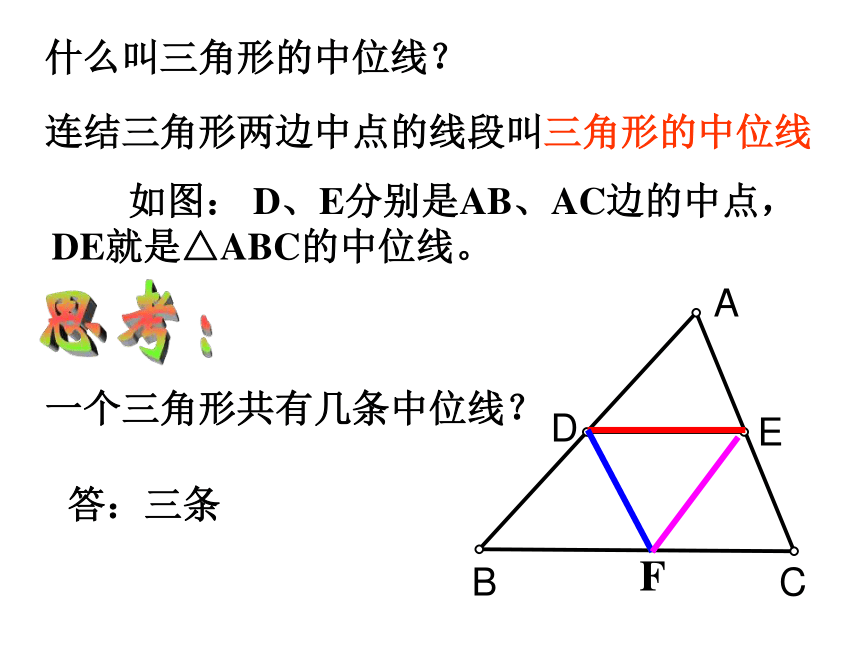
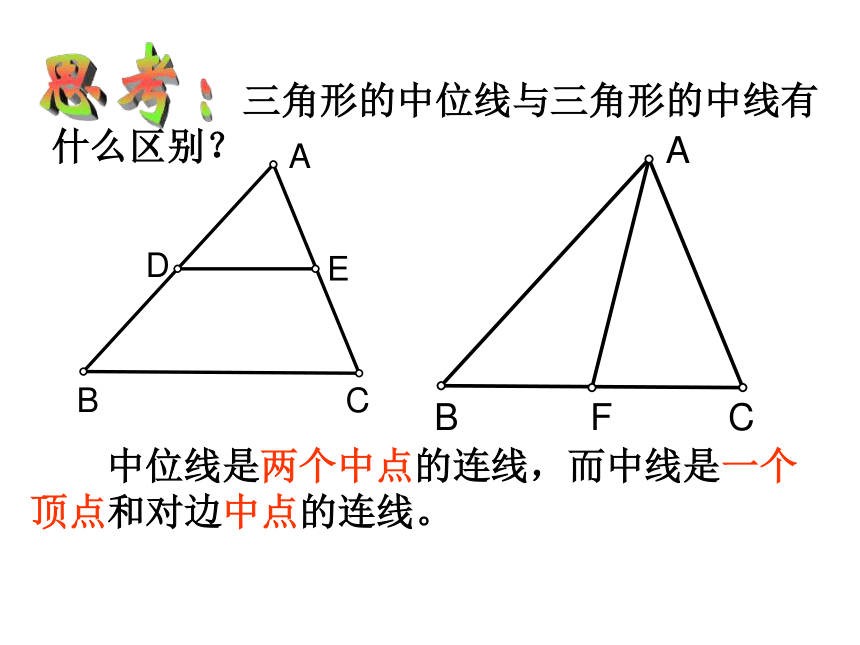
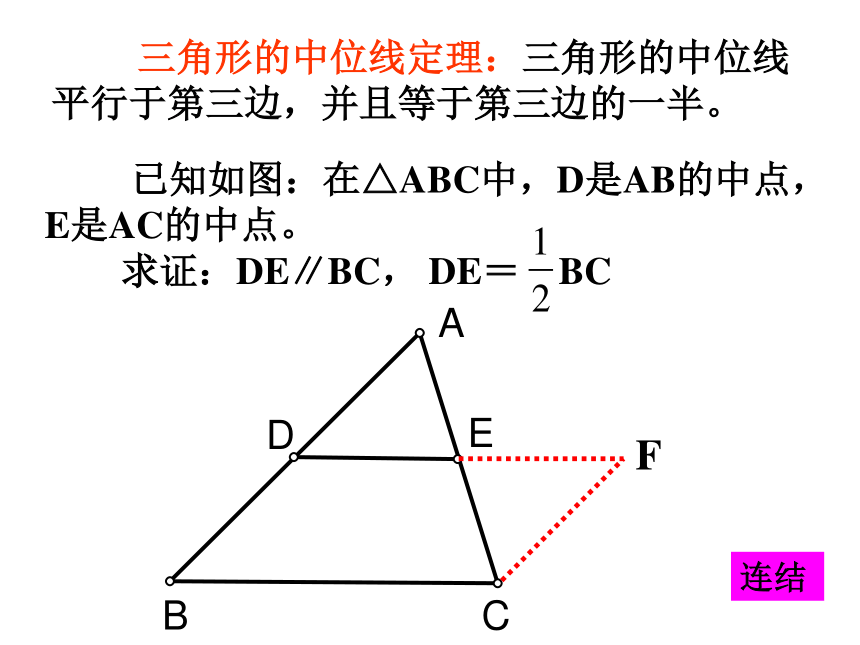
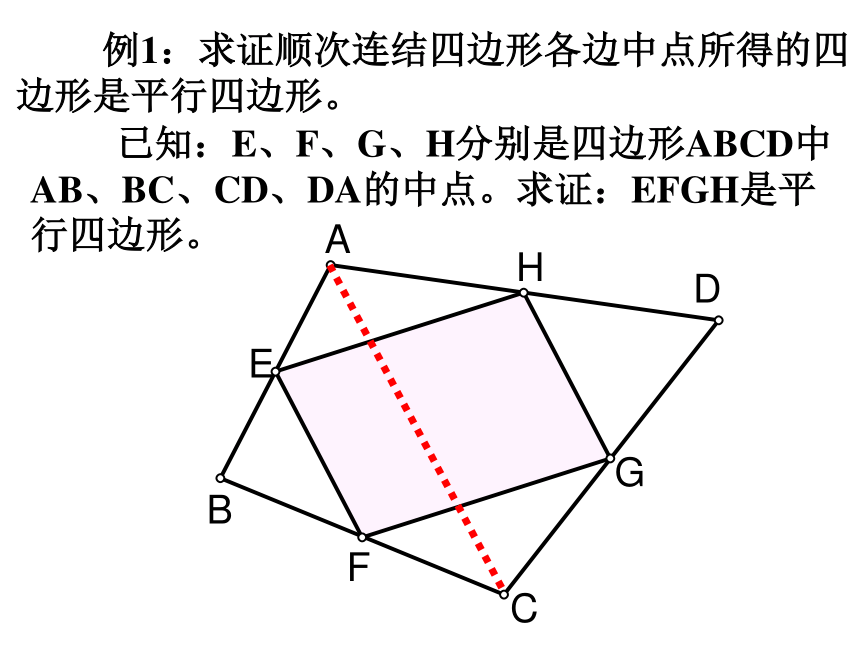
课件15张PPT。5.6三角形的中位线定理 A、B两地被建筑物阻隔，为了测量A、B 两地的距离，聪明的小明在地面上选一点C，连结CA、 CB ，并分别取它们的中点D、E，只要测量D、E两地的距离，就知道A、B两地的距离，你能明白其中的道理吗？你知道吗？ABCDE什么叫三角形的中位线？连结三角形两边中点的线段叫三角形的中位线 如图： D、E分别是AB、AC边的中点，DE就是△ABC的中位线。思考：一个三角形共有几条中位线？F答：三条 三角形的中位线与三角形的中线有什么区别？思考： 中位线是两个中点的连线，而中线是一个顶点和对边中点的连线。 三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半。F连结 例1：求证顺次连结四边形各边中点所得的四边形是平行四边形。 已知：E、F、G、H分别是四边形ABCD中AB、BC、CD、DA的中点。求证：EFGH是平行四边形。 任意四边形四边中点连线所得的四边形一定是平行四边形。熟记结论：1.（口答） A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN=20 m ,那么A、B两点的距离是多少？为什么？2. 已知：三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长。答案：15cm .答案：40 m . 例3：已知如图：在△ABC中，AB、BC、CA的中点分别是E、F、G，AD是高。求 证：∠EDG＝ ∠EFG。分析：EF是△ABC的中位线DG是Rt△ADC斜边上的中线∴EF＝DG你还想到了什么？反馈练习:（口答） 如图，点D、E、F分别是△ABC三边的中点， （1）如图1，DE=5，BC=？ （2）如图2，∠C=70o，则∠EDF=？ （3）图3中有几个平行四边形？ （4）图3中哪些三角形全等？ （5）若△DEF的周长为10，
则△ABC的周长为？△XYZ的周长呢？（6）若△ABC的面积为20，则△DEF的面积为？
△XYZ的面积为？ （7）图5中，AF与DE有什么关系？如何用语言叙述？ XYZ问题3如图，已知CE、CB分别是△ABC, △ADC 的中线，且AB=AC，试说明CD=2CEABCED在四边形ABCD中，AB=CD,E、F分别是AD、BC的中点，延长BA和CD分别交FE的延长线于点G、H,试猜想∠G与∠CHF的大小关系，并说明理由。动动脑ABCDEFGHM2 、例题例１　如图:直角△ABC中,CD是斜边AB的中线,
MN是中位线
求证:CD=MN证明: ∵ CD是斜边AB的中线
∵ MN是中位线∴ CD=MN
谢谢合作，下次再见！