初二数学5.4中心对称[下学期]

课件34张PPT。中心对称图形平阳昆阳二中陈春莲请仔细观察这幅剪纸作品的图案，你认为它有什么特点？你能指出对称轴？回顾与思考我们已学过哪些图形变换？轴对称变换、平移变换、
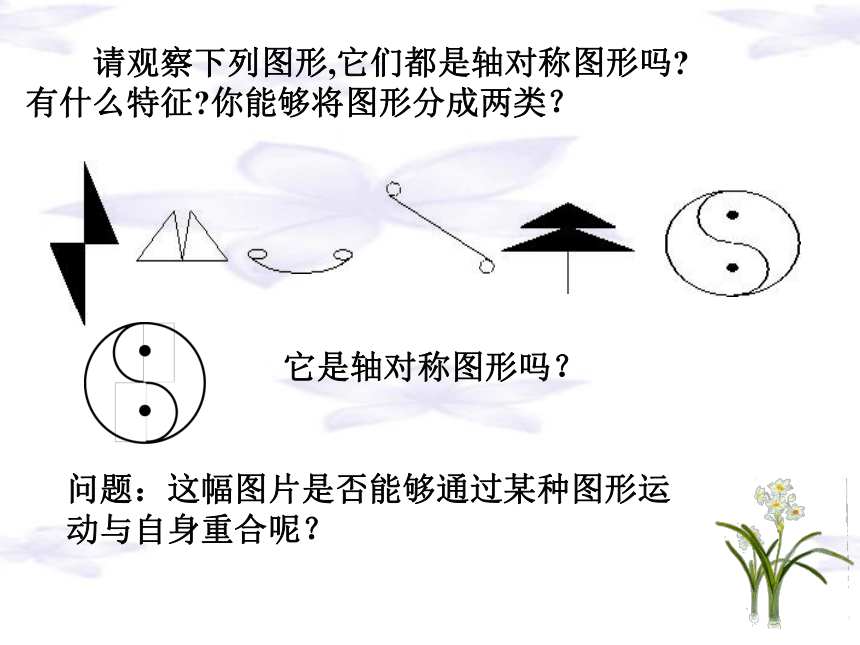
旋转变换、相似变换。这幅图案有哪些变换？轴对称变换。有旋转变换吗？90°、180°、270°。　　请观察下列图形,它们都是轴对称图形吗?
有什么特征?你能够将图形分成两类？
它是轴对称图形吗？问题：这幅图片是否能够通过某种图形运动与自身重合呢？合作学习、探索新知。
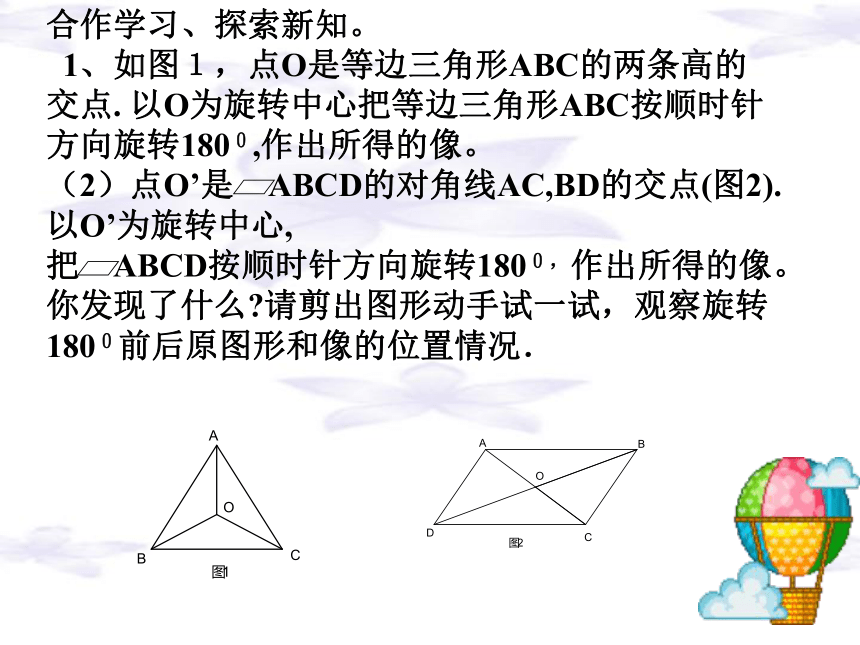
1、如图１，点O是等边三角形ABC的两条高的交点. 以O为旋转中心把等边三角形ABC按顺时针方向旋转180０,作出所得的像。
（2）点O’是　ABCD的对角线AC,BD的交点(图2).以O’为旋转中心,
把　ABCD按顺时针方向旋转180０，作出所得的像。
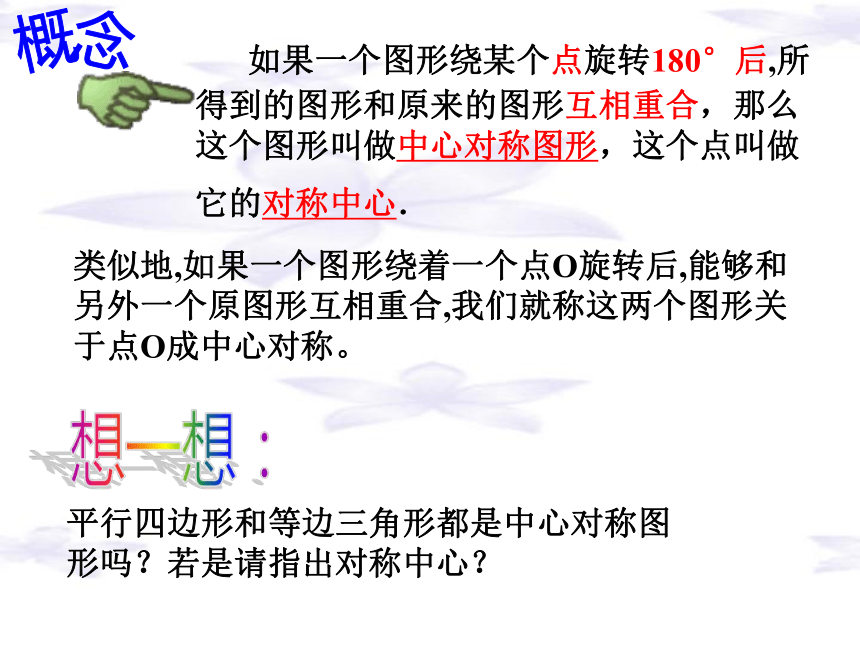
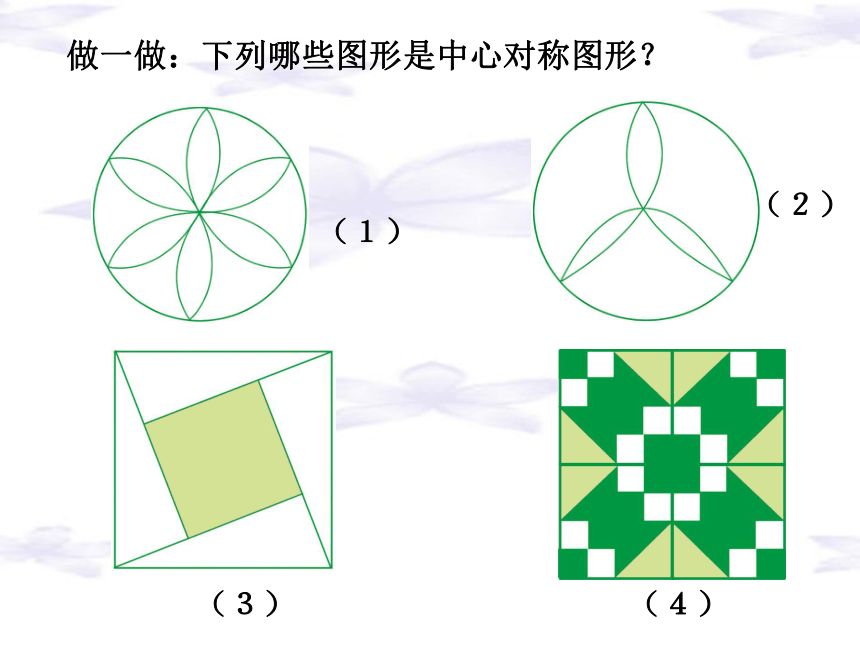
你发现了什么?请剪出图形动手试一试，观察旋转180０前后原图形和像的位置情况． 如果一个图形绕某个点旋转180°后,所得到的图形和原来的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心． 概念平行四边形和等边三角形都是中心对称图形吗？若是请指出对称中心？想一想：类似地,如果一个图形绕着一个点O旋转后,能够和另外一个原图形互相重合,我们就称这两个图形关于点O成中心对称。做一做：下列哪些图形是中心对称图形？（１）（２）（３）（４）中心对称图形的性质：
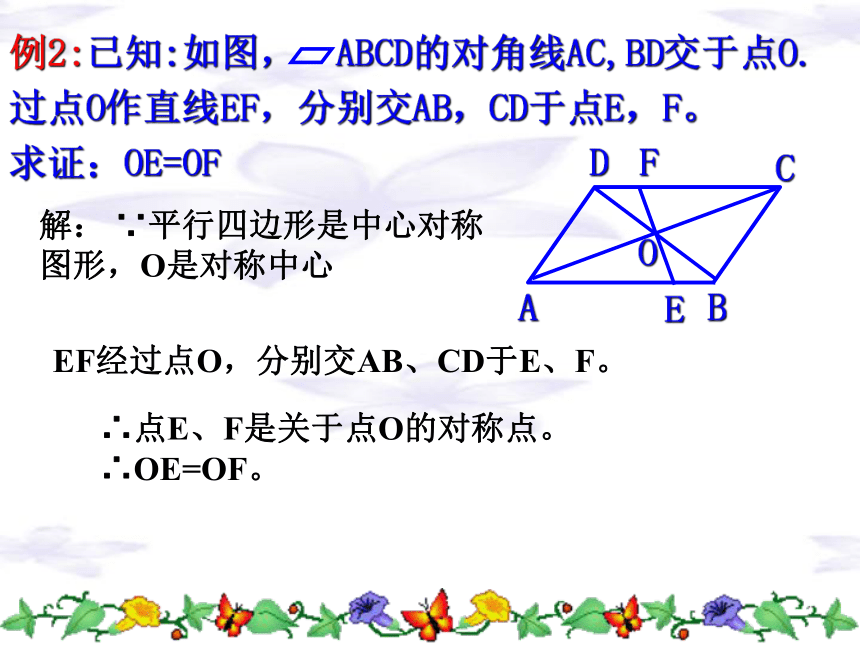
对称中心平分连结两个对称点的线段如右图，若A、B关于点O的成中心对称，∴点O是A、B的对称中心。反之，已知点A、点O，作点B，使点A、B关于以O为对称中心的对称点。EF经过点O，分别交AB、CD于E、F。解： ∵平行四边形是中心对称图形，O是对称中心∴点E、F是关于点O的对称点。
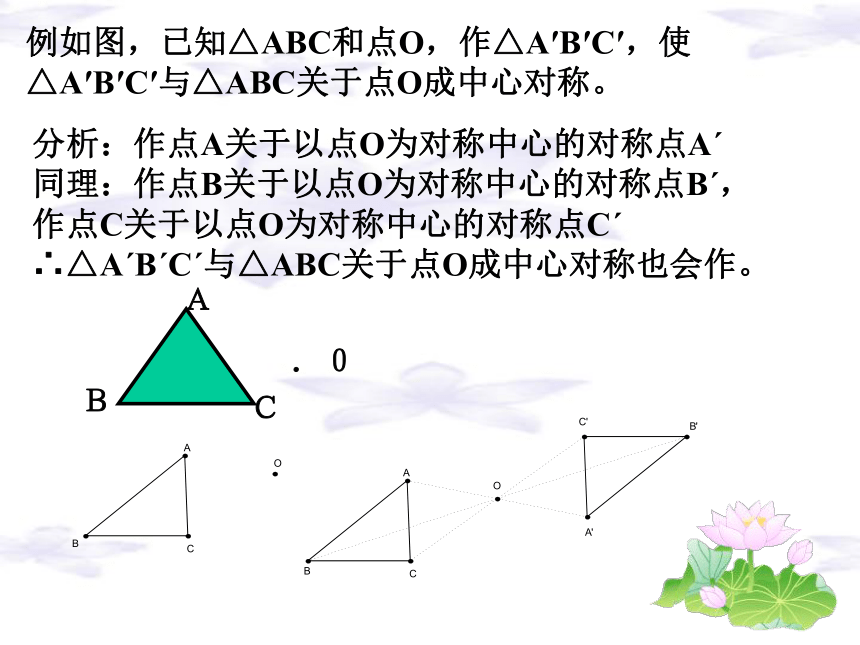
∴OE=OF。例如图，已知△ABC和点O，作△A′B′C′，使△A′B′C′与△ABC关于点O成中心对称。分析：作点A关于以点O为对称中心的对称点Aˊ
同理：作点B关于以点O为对称中心的对称点Bˊ，
作点C关于以点O为对称中心的对称点Cˊ
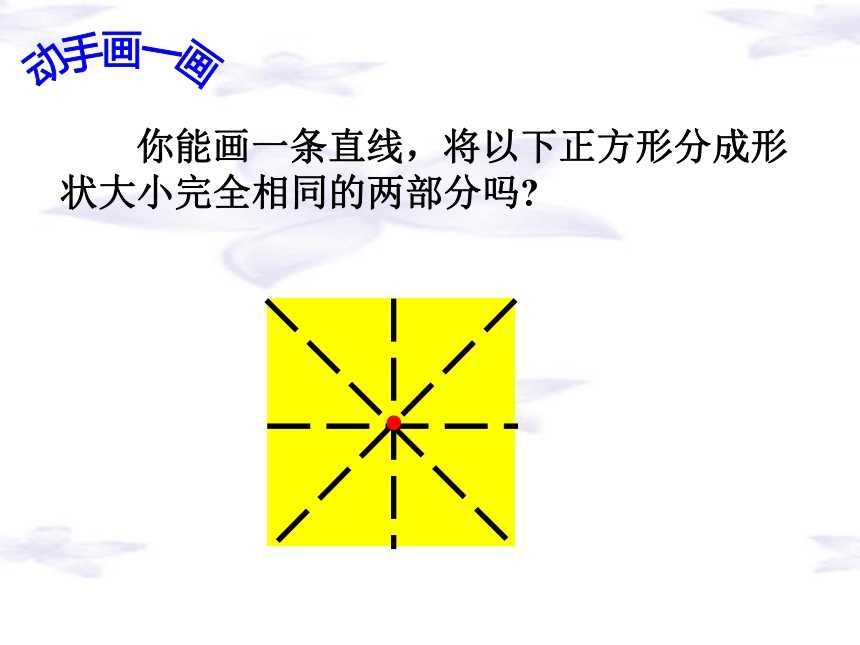
∴△AˊBˊCˊ与△ABC关于点O成中心对称也会作。．０ＡＣＢ动手画一画 你能画一条直线，将以下正方形分成形状大小完全相同的两部分吗?动手画一画动手转一转动手转一转动手找一找判断下列图形是不是中心对称图形 ： 练一练转一转，想一想·A·Ａ′·O　　中心对称图形上的每一对对应点所连成的线段都被对称中心平分 转一转，想一想动手摆一摆作业题：１、观察图形，并回答下面的问题：
（１）哪些只是轴对称图形？
（２）哪些只是中心对称图形？
（３）哪些既是轴对称图形，又是中心对称图形？（１）（３）（２）（４）（５）（６）（１）（２）（３）（４）（５）（６）２、下面图案是中心对称图形吗？若是请指出它们的对称中心，对于图（６），只要把图形绕整个圆的圆心旋转多少度，就能和原图重合。3、图中，不是中心对称图形的是（ ）ABCDB应用价值应用价值ＣＡＤＢＯ４、已知四边形ABCD和点O,作四边形A’B’C’D’,使四边形A’B’C’D’与四边形ABCD关于点O成中心对称。 中心对称图形与轴对称图形的不同之处为:中心对称图形 轴对称图形 有一个对称中心——点 有一条对称轴——直线 已知：下列命题中真命题的个数是（ ）
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3B1　 2 　3 　4 　5
2 　 3　 4 　 5 　6
3 　4 　 5 　6 　7
4 　5 　6 　　7 　8
5 　 6 　 7 　 8 　9应用价值应用价值应用价值1　 2 　3 　4 　5
2 　 3　 4 　 5 　6
3 　4 　 5 　6 　7
4 　5 　6 　　7 　8
5 　 6 　 7 　 8 　9通过这节课的学习，你有什么体会和收获？ 回顾小结