5.2平行四边形[下学期]

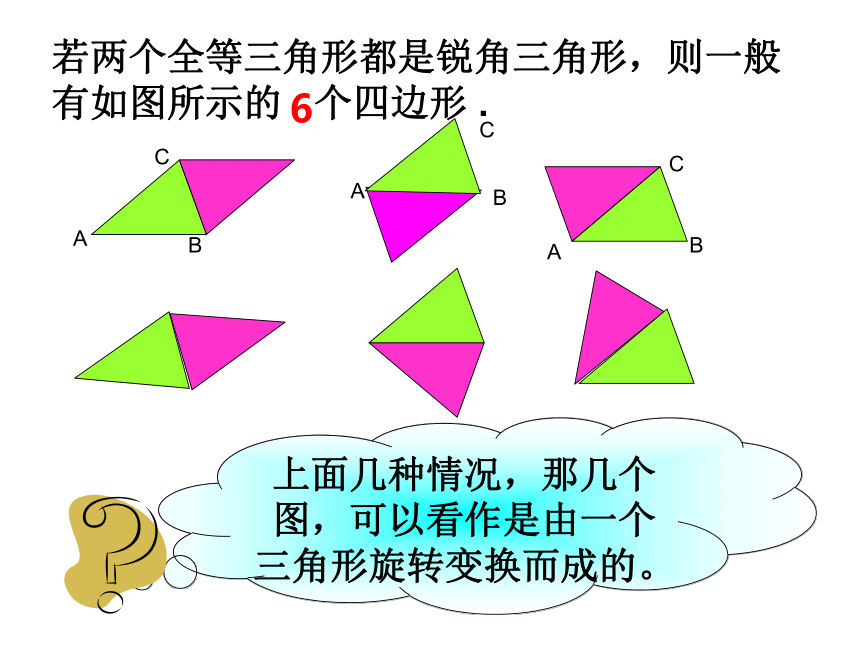
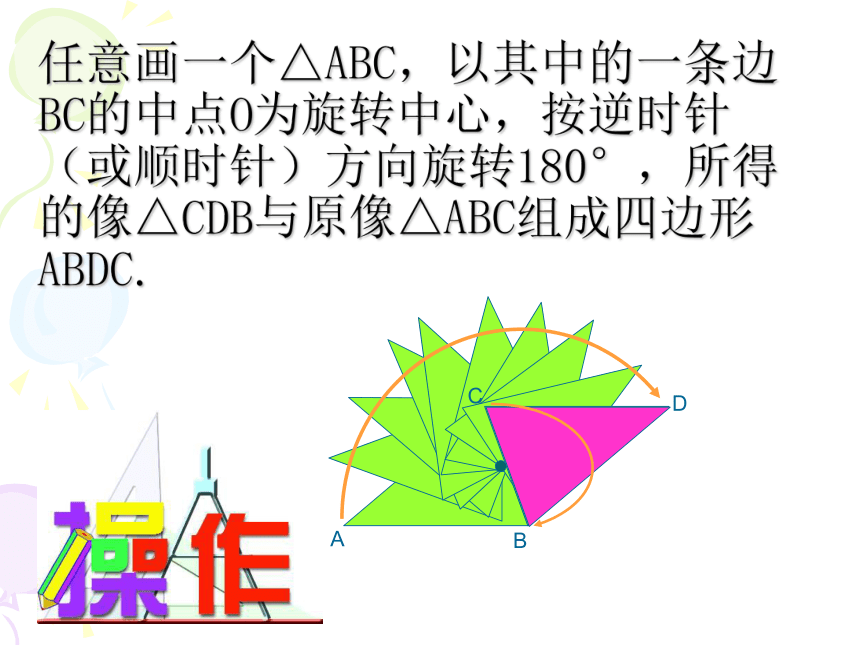
课件20张PPT。 浙教版 八年级（下）平行四边形任意剪两个全等的三角形，然后用这两个全等三角形拼四边形。你能拼出几种不同形状的四边形？ 请你剪一剪上面几种情况，那几个图，可以看作是由一个三角形旋转变换而成的。若两个全等三角形都是锐角三角形，则一般有如图所示的 个四边形 .ABCAACCBB6任意画一个△ABC，以其中的一条边BC的中点O为旋转中心，按逆时针（或顺时针）方向旋转180°，所得的像△CDB与原像△ABC组成四边形ABDC.ABC（1）找出这个四边形中相等的角；
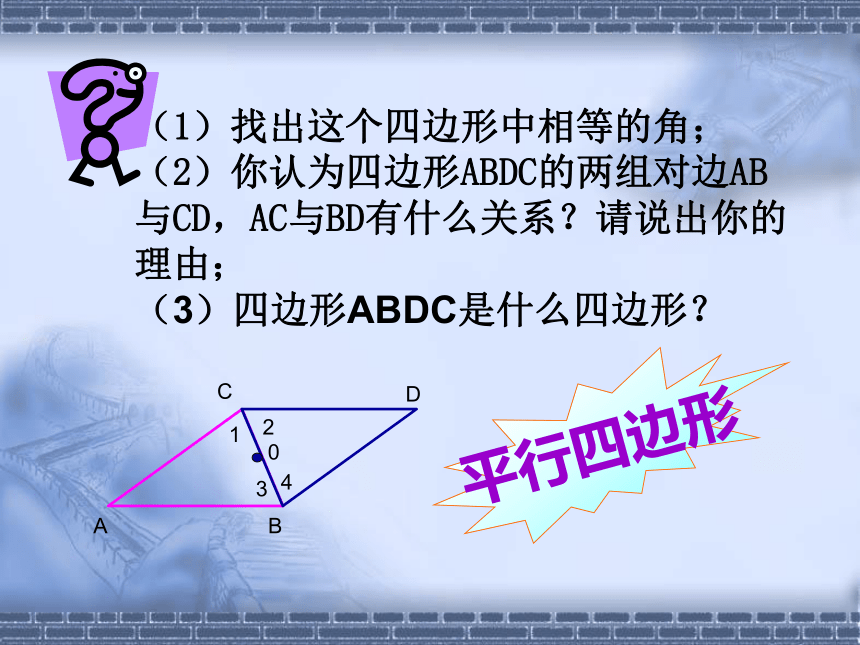
（2）你认为四边形ABDC的两组对边AB与CD，AC与BD有什么关系？请说出你的理由；
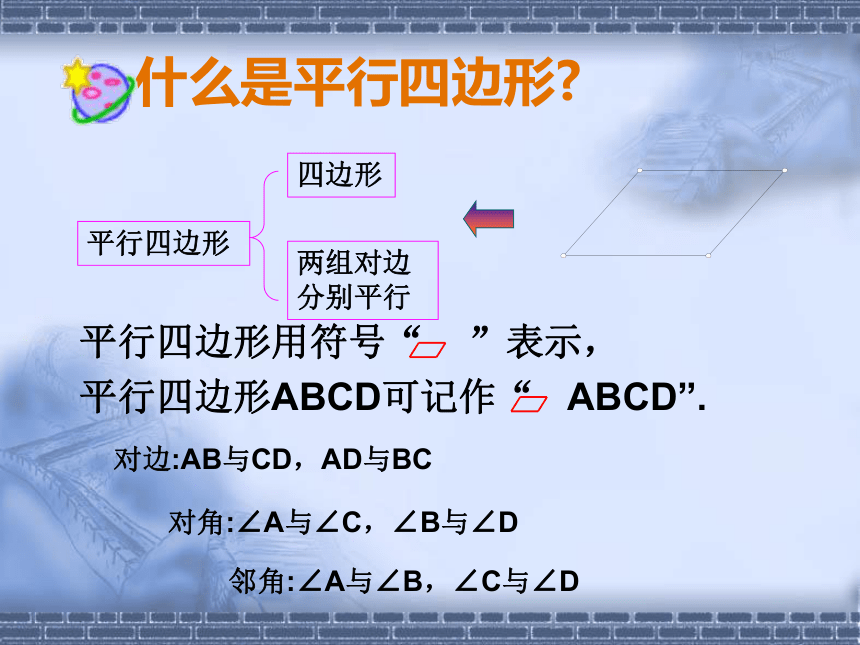
（3）四边形ABDC是什么四边形？平行四边形1234平行四边形用符号“ ”表示，
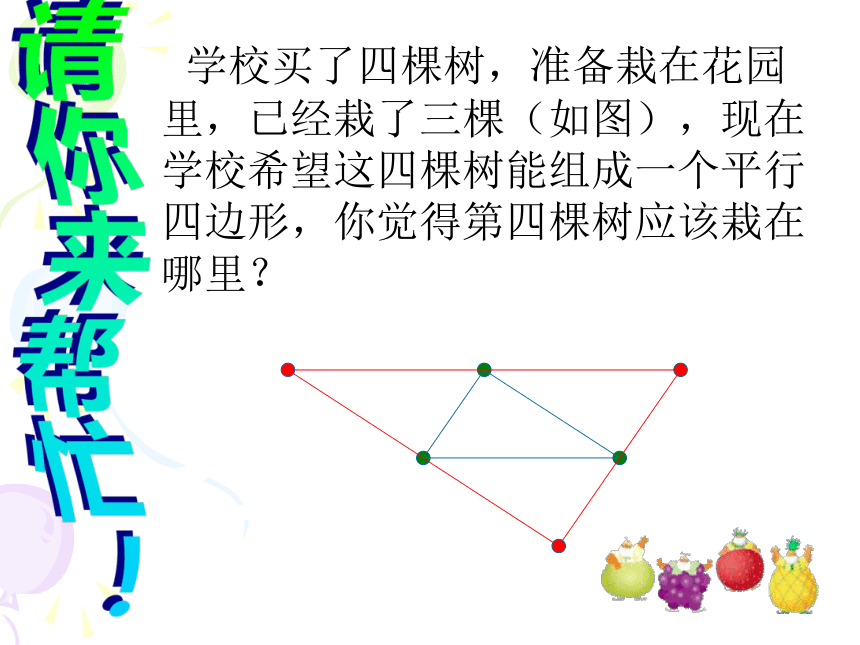
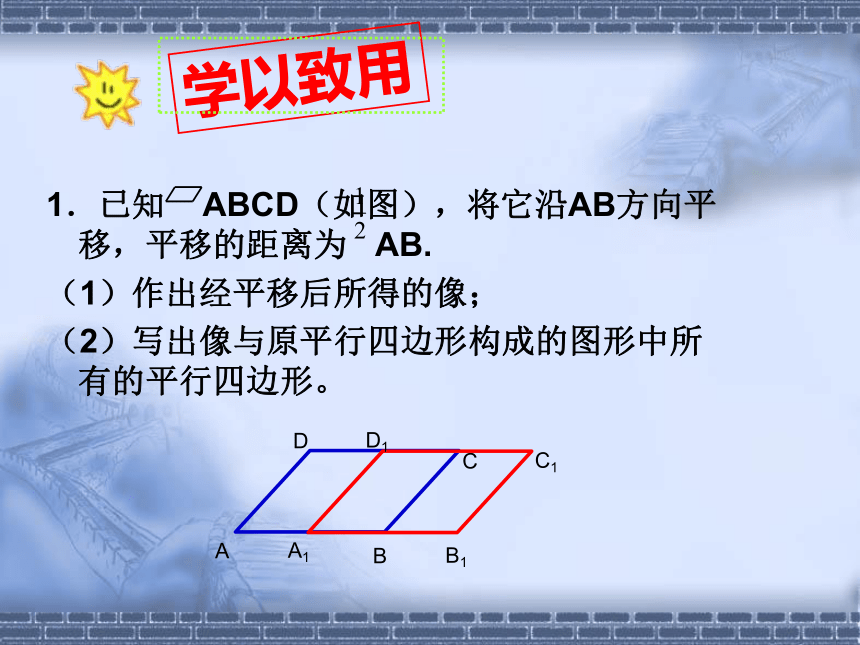
平行四边形ABCD可记作“ ABCD”. 什么是平行四边形?对角:∠A与∠C，∠B与∠D对边:AB与CD，AD与BC邻角:∠A与∠B，∠C与∠D两组对边分别平行四边形平行四边形请你来帮忙！ 学校买了四棵树，准备栽在花园里，已经栽了三棵（如图），现在学校希望这四棵树能组成一个平行四边形，你觉得第四棵树应该栽在哪里？1．已知 ABCD（如图），将它沿AB方向平移，平移的距离为 AB.
（1）作出经平移后所得的像；
（2）写出像与原平行四边形构成的图形中所有的平行四边形。学以致用2． ABCD中，EF∥AB，GH∥BC，EF、GH交于点K，写出图中所有的平行四边形：
（除 ABCD外）.学以致用3．已知：如图，将 ABCD作平移变换，得 A′B′C′D′. A′D′交CD于点E，A′B′交BC于点F.
求证：四边形A′FCE是平行四边形.学以致用1． ABCD中，AB∥ ，AD∥ .
2． ABCD中，∠A＋∠D＝ ，∠A＋∠B＝ ，
∠B＋∠C＝ ，∠C＋∠D＝ .
3．已知 ABCD中，∠A＝55°，则∠B＝ ，∠C＝ ，∠D＝ .
4．在 ABCD中，∠BAC＝26°，∠ACB＝34°，
则∠DAC＝ ，∠ACD＝ ，
∠D＝ ° 超级演练180o125°55 °125 °34 °26 °120180o180o180oCDBC例题：已知四边形ABCD是平行四边形，如图 所示，求证：∠A＝∠C，∠B＝∠D.证明: 如图,在 ABCD中,
ABCD,ADBC(平行四边形的定义)
∴∠A+ ∠D=180o, ∠C+ ∠D=180o
(两直线平行,同旁内角互补)
∴∠A= ∠C.
同理可得, ∠B＝∠D.
定理：平行四边形的对角相等。
即，在 ABCD中, ∠A＝∠C，∠B＝∠D.应用新知 课本P103作业题2,3,4平行四边形不稳定性的应用看一看本节课
你有什么收获？课堂小结1、平行四边形的定义：两组对边分别平行的四边形。
2、平行四边形的对角相等。
3、平行四边形的不稳定性在实际生活中的应用。
多 谢 指 导