第六章 特殊平行四边形与梯形教材分析[下学期]
文档属性
| 名称 | 第六章 特殊平行四边形与梯形教材分析[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-15 00:00:00 | ||
图片预览









文档简介
课件33张PPT。向同行学习,向专家致敬!瑞安安阳实验中学 吴时学 第六章 特殊平行四边形与梯形浙教版八年级下册一、教材内容三、教学目标二、教材地位四、教学建议一、教材内容:§6.1 矩形(共3课时)
§6.2 菱形(共2课时)
§6.3 正方形(共1课时)
§6.4 梯形(共2课时)
课题学习(简单平面图形的重心)(共1课时)
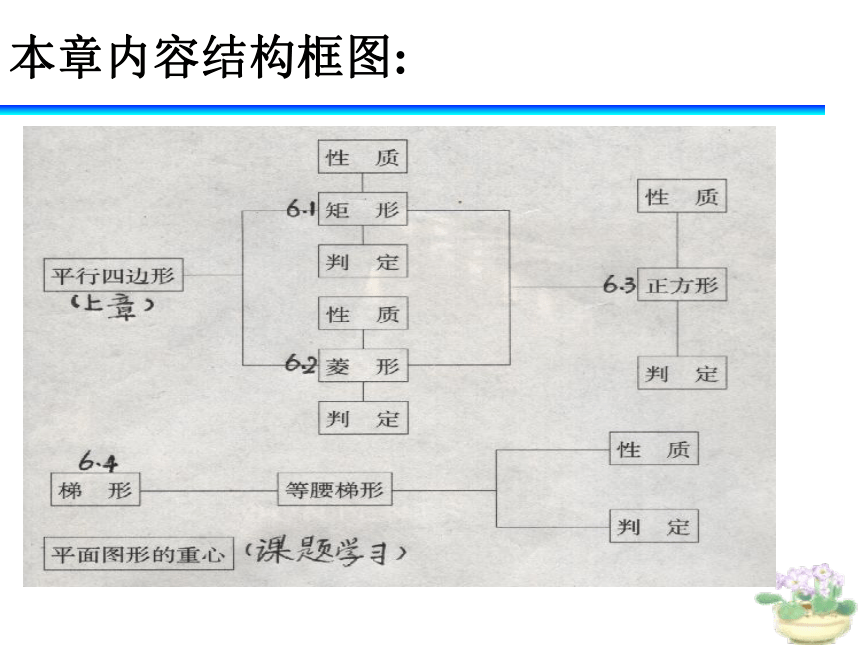
本章内容结构框图: (1)削弱了梯形中位线定理在教学中的地位;
(2)删掉了平行线等分线段定理的教学内容;
(3)增添了简单平面图形的重心的教学内容,沟通了学科之间的联系;
(4)加强了合作学习、动手操作、活动探究。与老教材的区别: “空间与图形”分四部分:实验几何(七年级上)——实验向论证过渡(七年级下至八年级上 )——几何证明(八年级下“命题与证明”、“平行四边形”、“特殊平行四边形与梯形”)——实验与推理综合运用(九年级)。二、教材地位: 八年级下册主要内容是论证几何,教材提出命题与证明,并通过“平行四边形”、“特殊平行四边形和梯形”的教学,使学生掌握综合法的几何证明格式,并学会表述。可见,“特殊平行四边形与梯形”的内容是论证几何的精华。1.本章教材在“空间与图形”部分的重要性:2.本章教材例举了充分的实例,说明了矩形、菱形、正方形和梯形在日常生活和生产实践中广泛应用。可见,学好本章内容,无论是进一步学习,还是参加生产实践,都有重要的意义.二、教材地位: 三、教学目标: 1、体会特殊平行四边形、等腰梯形概念的形成过程并掌握有关概念;
2、探索特殊平行四边形、等腰梯形的性质与判定的过程并掌握其性质与判定方法;
3、探索平面图形的重心的过程,了解平面图形的重心物理意义;
4、进一步提高逻辑推理和逻辑表达能力;
5、提高学生动手实验、操作的能力及探索的能力;
6、 体会在证明过程中所运用的归纳、类比和转化的数学思想方法。四、教学建议:1、通过观察有关特殊四边形及梯形的图片与多方面例举实例,让学生感受几何的意义及文化价值。四、教学建议:2、注重知识的内在联系,加强知识的系统性。四、教学建议:3、合理利用 “合作学习”,营造宽松的学习环境,让学生积极参与,达到生生合作、师生互动,从而获得概念、性质与定理。6.2菱形(1):矩形.gsp6.1矩形(1):6.2菱形(2):四、教学建议:4、合理增加剪纸、分割、拼图方面的练习,培养动手操作的能力。P138课内练习3、将一张平行四边形的纸片剪上一刀然后将所分成的两部分作适当的图像变换,拼成一个矩形。说明你的剪法。P142作业题6、将两个全等的等腰三角形(非正三角形)纸片拼成一个平行四边形,有哪些拼法?怎么拼,才是菱形?说明拼法,画出示意图。P146作业题2、将一张正方形纸片沿虚线折一次得图(1),再对折一次得图(2),然后用剪刀沿图(2)中的虚线剪去一个角,请画出打开后的形状。(1)(2)1、某中学有一块正方形花园,现打算将它分成全等的4块土地,种上4种花草。请你利用所学知识设计出4种不同的方案。(在图中做上必要的记号)
参考例题:2、请将四个全等直角梯形(如图),拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法).
3、如图,把边长为2的正方形剪成四个全等的直角三角形。请用这四个直角三角形拼成符合下列要求的图形,并标上必要的记号。(1)不是正方形的菱形(1个);(2)不是正方形的矩形(1个);(4)不是矩形和菱形的平行四边形(1个);(5)不是梯形和平行四边形形的凸四边形(1个)。(3)梯形(1个);4、小明家用瓷砖装修卫生间,还有一块墙角面未完工(如图甲所示),他想在现有的六块瓷砖余料中(如图乙所示)挑选2块或3块余料进行铺设,请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图,并标出所选用每块余料的编号)。四、教学建议:5、注重对证明思路的启发,提倡证明方法的多样性,并讲究问题的变式训练。1、在6.1矩形(3)中的定理“直角三角形斜边上的中线等于斜边的一半”证明时,应结合矩形的知识适当提示线段倍分的证题思路。比如:变式:已知:线段EF,GH都过矩形对角线的交点O,且EF⊥GH。求证:四边形EGFH是菱形。2、6.2菱形(2)中的例2:3、6.4梯形(1)中的例1:4、梯形(2)中的例2:四、教学建议:6、注意数学思想方法(转化思想)在教学中的渗透。四、教学建议:7、针对教材特点,精心设计活动探究的方案,重视问题探究的过程。条件探究题:(6.2菱形(2))菱形(2)探究活动.gsp设计:课前每小组准备一张符合条件纸片:
(1)指导学生怎样设计矩形,再剪出来;
(2)你剪出来的图形一定是矩形吗?你能说明理由吗?
(3)把你的矩形与别人比较一下,一样吗?
( 4)你有什么结论?
6.1 矩形(2)例2:结论探究题:问题:将任意梯形纸片只剪一刀分成两部分,使这两部分能拼成一个三角形,你能办到吗?H6.4 梯形(1):可把第146页课内练习3拓展为探究活动:(1)求证:依次连接正方形各边中点所成的四边形是正方形。
(2)依次连接菱形或矩形各边中点能得到一个什么图形先画一画,再证明。
(3)依次连接平行四边形各边中点呢?
(4)依次连接四边形各边中点所得到的新四边形形状与哪些线段有关系?有怎样的关系?请探究。这样安排可以引导学生对方法和规律的总结。
同时也进一步的把结论向一般化推广。在教学中应该把证明思路向对角线方面引导。中点四边形.gsp关于中点四边形的探究: 本节课内容与科学有着密切的联系,但在教学中不能把它上成力学课,而应通过学生亲手做实验深刻感受线段的重心,从而了解平面图形重心的物理定义,达到抽象出对其他平面图形重心的研究。 确定重心的方法可以留给学生去探究。
课题学习:简单平面图形的重心 本节课的确定重心的方法可以让学生去尝试、去探究。教师可在最后概括确定重心的方法:
(1)等分面积法;(2)悬挂法。合作学习:实验探索四边形的重心的位置设计建议:
(1)以5人为一组,每组设组长一名。
(2)每小组课前 分工准备平行四边形、矩形、菱形、正方形、梯形纸版片各一个,细线、大头针若干。
(3)小组在实验前共同讨论、估计重心的位置。
(4)实验时,小组每位成员分工负责一个图形的实验(轮流进行)其他成员在旁观察或协助。
(5)组长负责汇总实验记录,填写报告单。与重心联系的知识:平分面积。(1)平分三角形的面积:中线。(2)平分平行四边形的面积:过对角线交点的直线。(3)平分梯形的面积:过上、下底的中点连线的中点的直线(与上、下底相交)。谢谢大家
敬请指导
§6.2 菱形(共2课时)
§6.3 正方形(共1课时)
§6.4 梯形(共2课时)
课题学习(简单平面图形的重心)(共1课时)
本章内容结构框图: (1)削弱了梯形中位线定理在教学中的地位;
(2)删掉了平行线等分线段定理的教学内容;
(3)增添了简单平面图形的重心的教学内容,沟通了学科之间的联系;
(4)加强了合作学习、动手操作、活动探究。与老教材的区别: “空间与图形”分四部分:实验几何(七年级上)——实验向论证过渡(七年级下至八年级上 )——几何证明(八年级下“命题与证明”、“平行四边形”、“特殊平行四边形与梯形”)——实验与推理综合运用(九年级)。二、教材地位: 八年级下册主要内容是论证几何,教材提出命题与证明,并通过“平行四边形”、“特殊平行四边形和梯形”的教学,使学生掌握综合法的几何证明格式,并学会表述。可见,“特殊平行四边形与梯形”的内容是论证几何的精华。1.本章教材在“空间与图形”部分的重要性:2.本章教材例举了充分的实例,说明了矩形、菱形、正方形和梯形在日常生活和生产实践中广泛应用。可见,学好本章内容,无论是进一步学习,还是参加生产实践,都有重要的意义.二、教材地位: 三、教学目标: 1、体会特殊平行四边形、等腰梯形概念的形成过程并掌握有关概念;
2、探索特殊平行四边形、等腰梯形的性质与判定的过程并掌握其性质与判定方法;
3、探索平面图形的重心的过程,了解平面图形的重心物理意义;
4、进一步提高逻辑推理和逻辑表达能力;
5、提高学生动手实验、操作的能力及探索的能力;
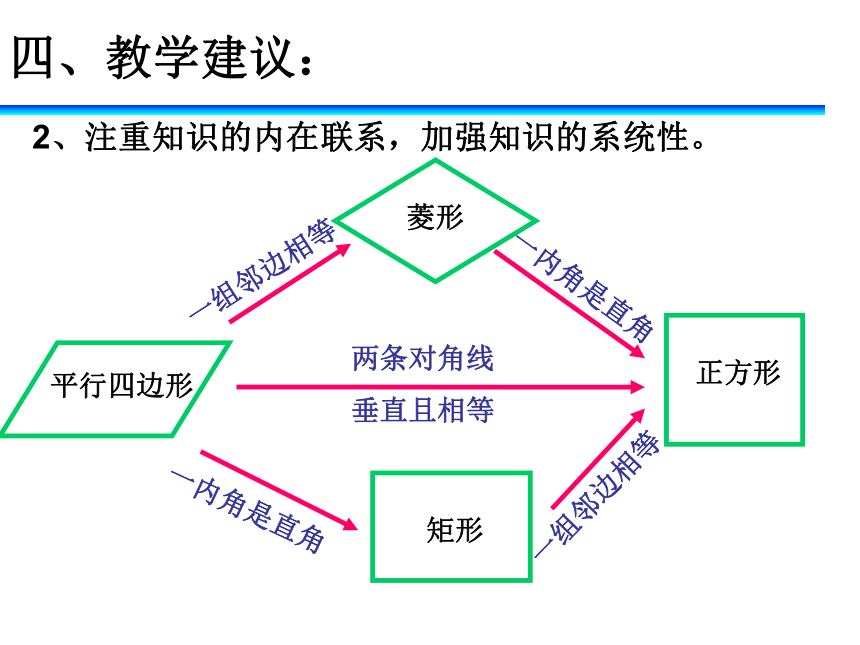
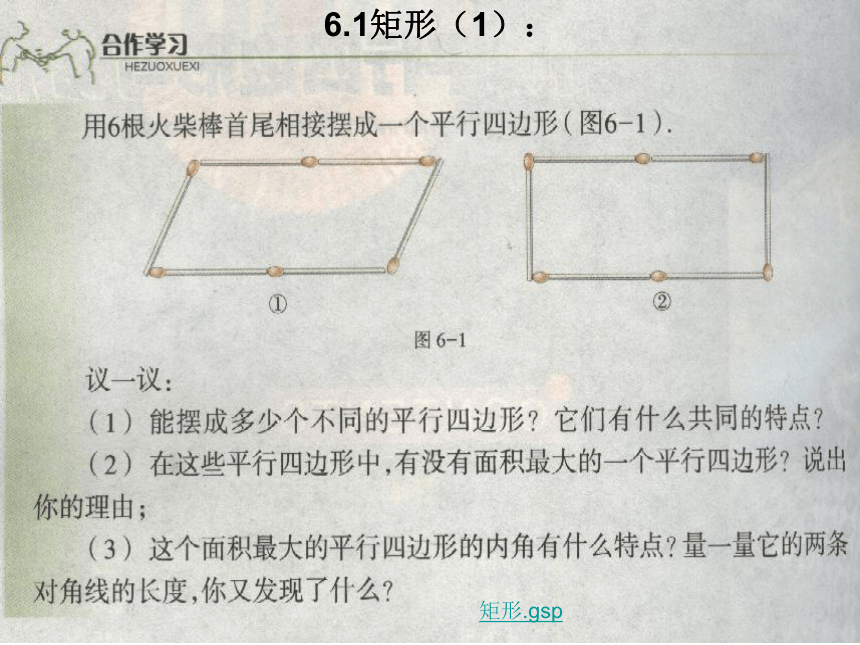
6、 体会在证明过程中所运用的归纳、类比和转化的数学思想方法。四、教学建议:1、通过观察有关特殊四边形及梯形的图片与多方面例举实例,让学生感受几何的意义及文化价值。四、教学建议:2、注重知识的内在联系,加强知识的系统性。四、教学建议:3、合理利用 “合作学习”,营造宽松的学习环境,让学生积极参与,达到生生合作、师生互动,从而获得概念、性质与定理。6.2菱形(1):矩形.gsp6.1矩形(1):6.2菱形(2):四、教学建议:4、合理增加剪纸、分割、拼图方面的练习,培养动手操作的能力。P138课内练习3、将一张平行四边形的纸片剪上一刀然后将所分成的两部分作适当的图像变换,拼成一个矩形。说明你的剪法。P142作业题6、将两个全等的等腰三角形(非正三角形)纸片拼成一个平行四边形,有哪些拼法?怎么拼,才是菱形?说明拼法,画出示意图。P146作业题2、将一张正方形纸片沿虚线折一次得图(1),再对折一次得图(2),然后用剪刀沿图(2)中的虚线剪去一个角,请画出打开后的形状。(1)(2)1、某中学有一块正方形花园,现打算将它分成全等的4块土地,种上4种花草。请你利用所学知识设计出4种不同的方案。(在图中做上必要的记号)
参考例题:2、请将四个全等直角梯形(如图),拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法).
3、如图,把边长为2的正方形剪成四个全等的直角三角形。请用这四个直角三角形拼成符合下列要求的图形,并标上必要的记号。(1)不是正方形的菱形(1个);(2)不是正方形的矩形(1个);(4)不是矩形和菱形的平行四边形(1个);(5)不是梯形和平行四边形形的凸四边形(1个)。(3)梯形(1个);4、小明家用瓷砖装修卫生间,还有一块墙角面未完工(如图甲所示),他想在现有的六块瓷砖余料中(如图乙所示)挑选2块或3块余料进行铺设,请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图,并标出所选用每块余料的编号)。四、教学建议:5、注重对证明思路的启发,提倡证明方法的多样性,并讲究问题的变式训练。1、在6.1矩形(3)中的定理“直角三角形斜边上的中线等于斜边的一半”证明时,应结合矩形的知识适当提示线段倍分的证题思路。比如:变式:已知:线段EF,GH都过矩形对角线的交点O,且EF⊥GH。求证:四边形EGFH是菱形。2、6.2菱形(2)中的例2:3、6.4梯形(1)中的例1:4、梯形(2)中的例2:四、教学建议:6、注意数学思想方法(转化思想)在教学中的渗透。四、教学建议:7、针对教材特点,精心设计活动探究的方案,重视问题探究的过程。条件探究题:(6.2菱形(2))菱形(2)探究活动.gsp设计:课前每小组准备一张符合条件纸片:
(1)指导学生怎样设计矩形,再剪出来;
(2)你剪出来的图形一定是矩形吗?你能说明理由吗?
(3)把你的矩形与别人比较一下,一样吗?
( 4)你有什么结论?
6.1 矩形(2)例2:结论探究题:问题:将任意梯形纸片只剪一刀分成两部分,使这两部分能拼成一个三角形,你能办到吗?H6.4 梯形(1):可把第146页课内练习3拓展为探究活动:(1)求证:依次连接正方形各边中点所成的四边形是正方形。
(2)依次连接菱形或矩形各边中点能得到一个什么图形先画一画,再证明。
(3)依次连接平行四边形各边中点呢?
(4)依次连接四边形各边中点所得到的新四边形形状与哪些线段有关系?有怎样的关系?请探究。这样安排可以引导学生对方法和规律的总结。
同时也进一步的把结论向一般化推广。在教学中应该把证明思路向对角线方面引导。中点四边形.gsp关于中点四边形的探究: 本节课内容与科学有着密切的联系,但在教学中不能把它上成力学课,而应通过学生亲手做实验深刻感受线段的重心,从而了解平面图形重心的物理定义,达到抽象出对其他平面图形重心的研究。 确定重心的方法可以留给学生去探究。
课题学习:简单平面图形的重心 本节课的确定重心的方法可以让学生去尝试、去探究。教师可在最后概括确定重心的方法:
(1)等分面积法;(2)悬挂法。合作学习:实验探索四边形的重心的位置设计建议:
(1)以5人为一组,每组设组长一名。
(2)每小组课前 分工准备平行四边形、矩形、菱形、正方形、梯形纸版片各一个,细线、大头针若干。
(3)小组在实验前共同讨论、估计重心的位置。
(4)实验时,小组每位成员分工负责一个图形的实验(轮流进行)其他成员在旁观察或协助。
(5)组长负责汇总实验记录,填写报告单。与重心联系的知识:平分面积。(1)平分三角形的面积:中线。(2)平分平行四边形的面积:过对角线交点的直线。(3)平分梯形的面积:过上、下底的中点连线的中点的直线(与上、下底相交)。谢谢大家
敬请指导
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
