6.2菱形（1）[下学期]

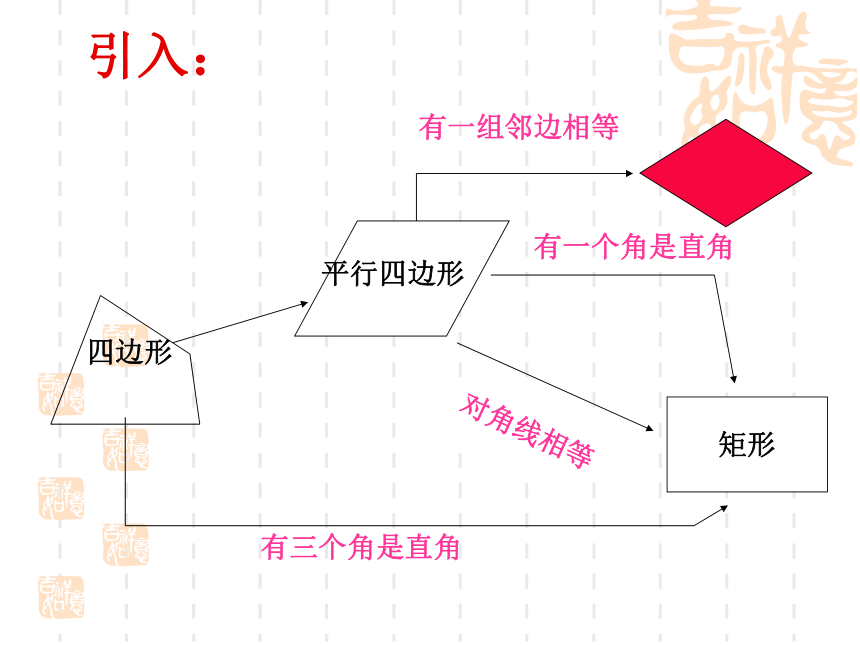
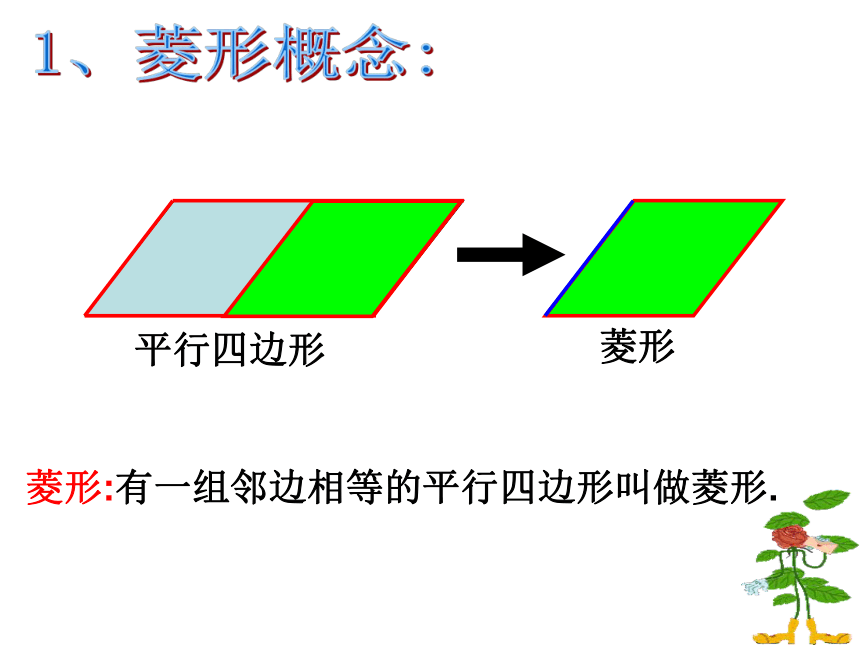
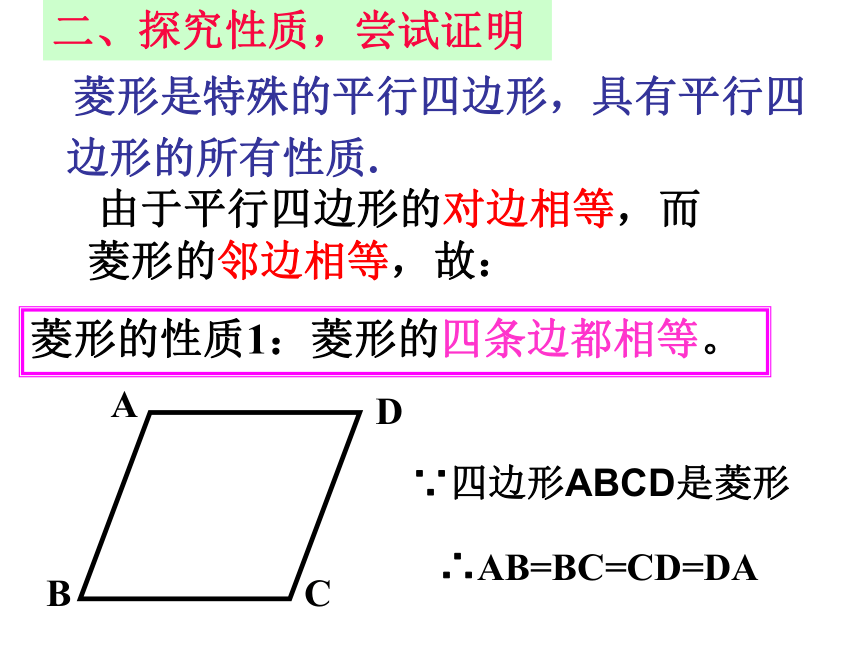
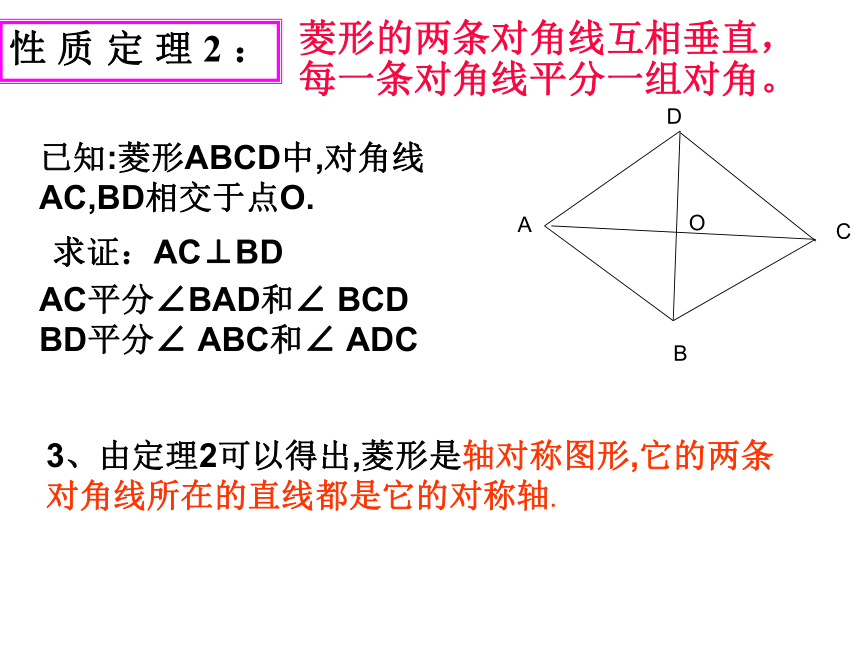
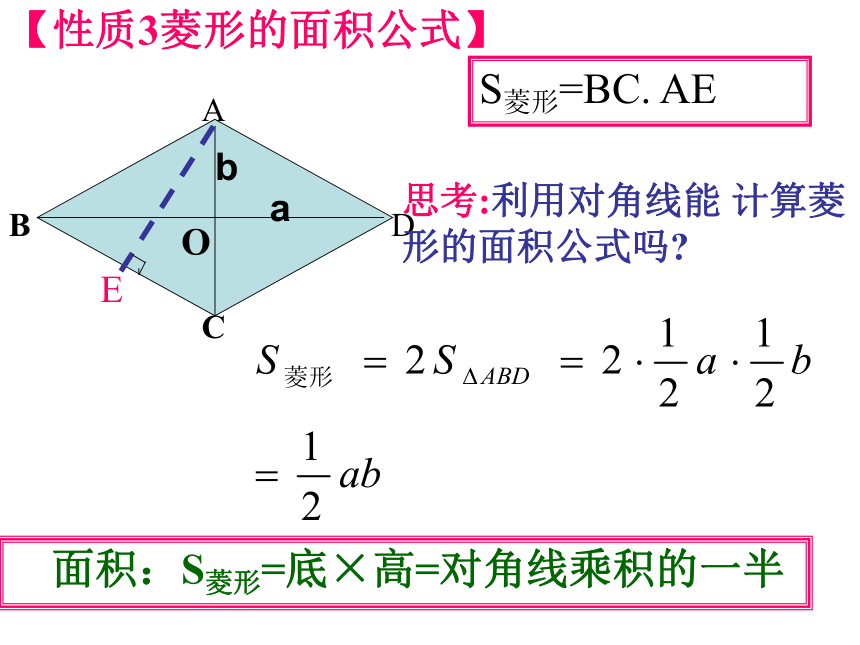
课件20张PPT。欢迎各位老师莅临指导！知识回顾:矩形的定义：有一个角是直角的平行四边形。矩形的性质矩形的判定具有平行四边形的一切特征四个角都是直角对角线相等的平行四边形对角线相等且平分有一个角是直角的平行四边形有三个角是直角的四边形对角线相等且平分的四边形引入：矩形有一个角是直角对角线相等有三个角是直角6.2(1) 菱形孙安娜平行四边形菱形菱形:有一组邻边相等的平行四边形叫做菱形.1、菱形概念:菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上. 由于平行四边形的对边相等，而菱形的邻边相等，故：菱形的性质1：菱形的四条边都相等。 菱形是特殊的平行四边形，具有平行四边形的所有性质.二、探究性质，尝试证明∵四边形ABCD是菱形∴AB=BC=CD=DA3、由定理2可以得出,菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴.菱形的两条对角线互相垂直，每一条对角线平分一组对角。性质定理2：【性质3菱形的面积公式】ABCDOES菱形=BC. AE思考:利用对角线能 计算菱形的面积公式吗? 面积：S菱形=底×高=对角线乘积的一半ab角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分对称性中心对称图形角边线对称性中心对称图形,轴对称图形菱形的对边平行,四条边相等菱形的两组对角分别相等菱形的两条对角线互相垂直平分，每一条对角线平分一组对角。二、菱形的性质归纳..三、运用性质，提高能力:解:∵四边形ABCD是菱形,
∴AB=AD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°
∴∠BAD=60°∴ABD是等边三角形.
AB=BD=6又∵OB=OD=3(平行四边形的对角线互相平分)
AC⊥BD(菱形的对角线互相垂直)
由勾股定理,得AO=
AC=2AO= 例2：如图四边形ABCD是边长为13cm的菱形，对角线长BD为10cm，求
（1）对角线AC的长
（2）菱形ABCD的面积
三、运用性质，提高能力:1.菱形具有而矩形不一定有的性质是( )
(A)对角线互相平分 (B)四条边都相等
(C)对角相等 (D)邻角互补2.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F.
求证:AE=AF.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F且E,F分别是BC,CD的中点,求菱形各个内角的度数.
四、巩固练习，拓展知识3.已知:在菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.求证:(1) △ABE≌△ADF;
(2) ∠AEF=∠AFE四、巩固练习，拓展知识4.在菱形ABCD中,CE⊥AB于E,已知∠BCE=30°,CE=3cm.求菱形ABCD的周长和面积.5.如图，菱形ABCD的边长为4cm，∠BAD＝1200。对角线AC、BD相交于点O，求这个菱形的对角线长和面积。解：菱形ABCD 中,∵ ∠BAD＝1200∴∠BAC＝600
又∵ AB ＝B C∴ △ BAC是等边三角形∴ AC ＝ 4cm对边平行四条边都相等中心对称图形轴对称图形对角相等对角线互相垂直对角线互相平分每一条对角线平分一组对角用列表形式小结出菱形的性质五、归纳小结,提炼知识1、底乘以高思考题 近几年，一些大城市里流行一种新式的衣帽架，它是用木条构成的几个连续的菱形（如图），每个顶点处都有一个挂钩，不仅美观而且实用，你能根据形状，说出它的好处和固定方法吗？答：好处（1）利用四边形的不稳定性，可以根据需要改变挂钩间的距离（2）利用平行四边形对边平行的原理，最后可以使平行木条完全靠拢，收起来不占地方。固定的方法：任选两个不在同一木条上的顶点固定就可以了。
谢谢大家!6.已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AB=1。
求（1）∠ABC的度数；
（2）对角线AC、BD的长；
（3）菱形ABCD的面积。