菱形的判定[下学期]

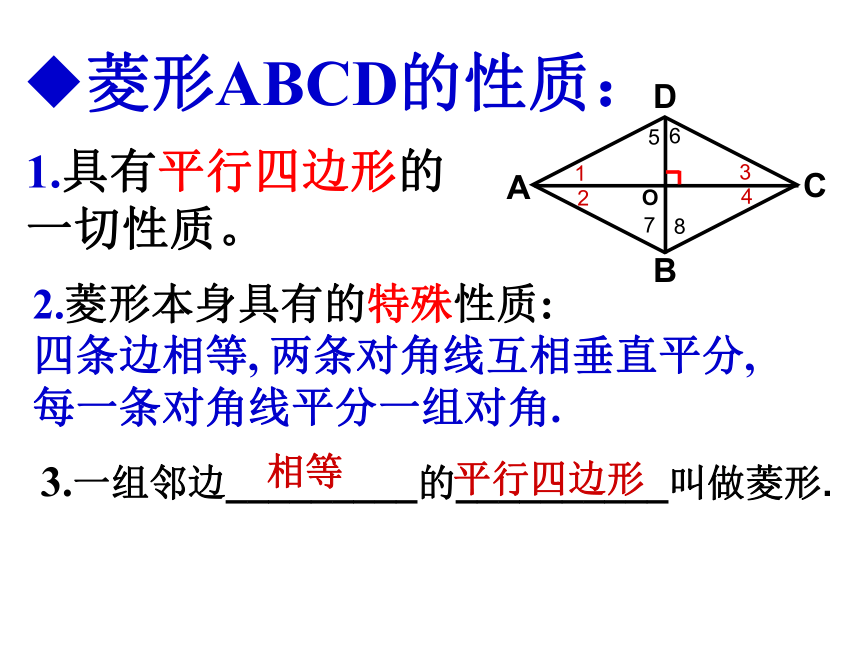
课件16张PPT。梅花香自苦寒来宝剑锋从磨砺出菱形(2)菱形ABCD的性质：1.具有平行四边形的一切性质。2.菱形本身具有的特殊性质: 四条边相等, 两条对角线互相垂直平分, 每一条对角线平分一组对角. 3.一组邻边_________的__________叫做菱形.
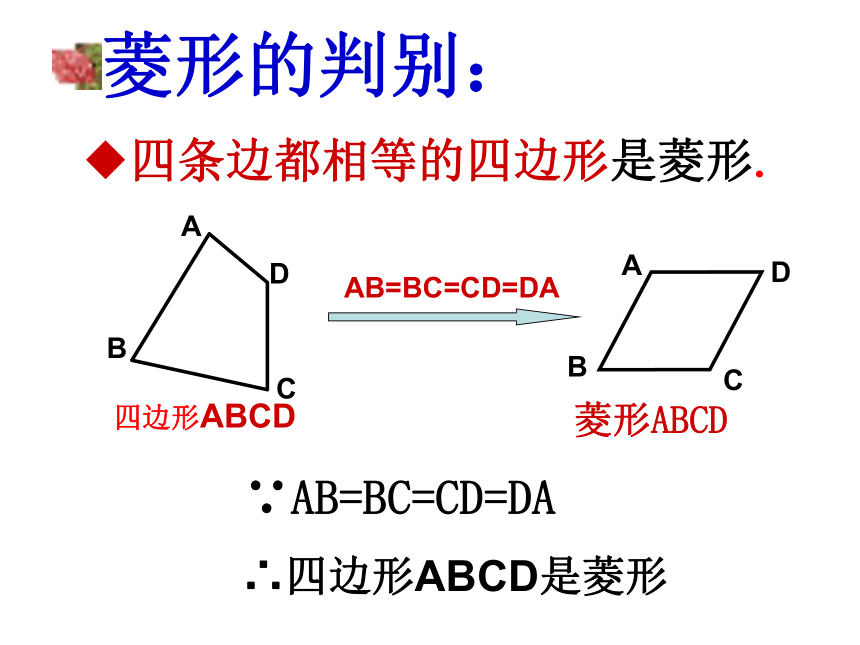
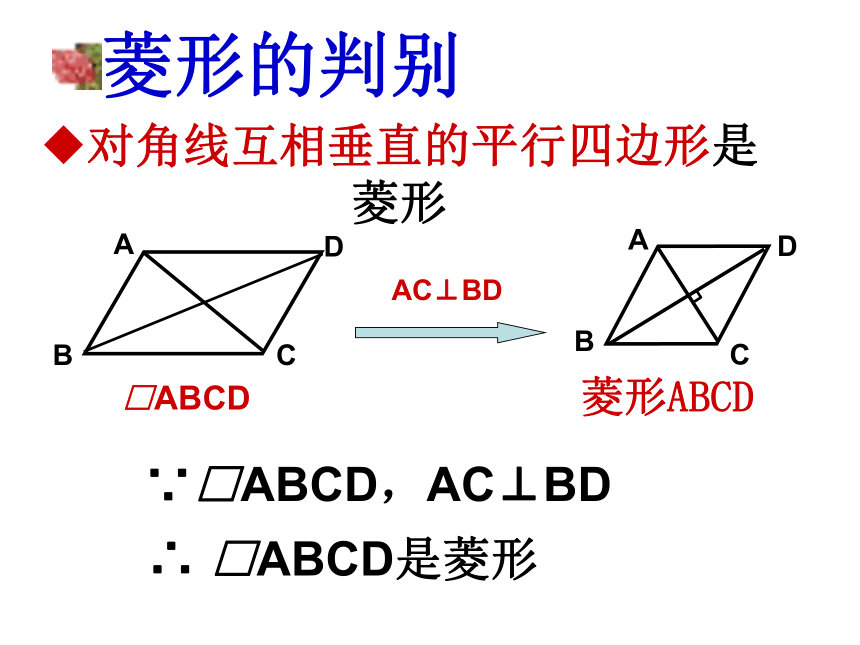
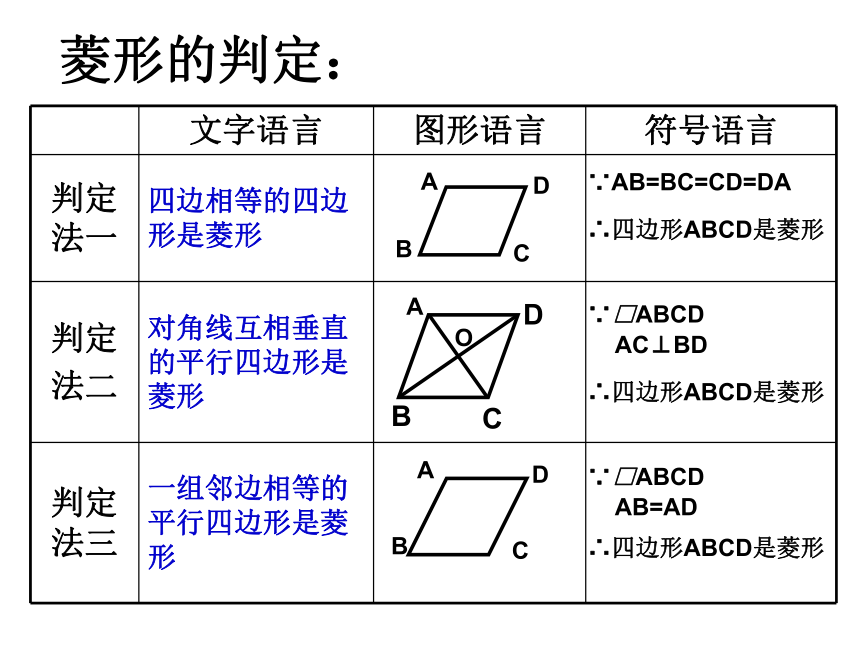
O相等平行四边形想一想（1） 把一个一般的四边形作如下变化，请问得到的四边形是菱形吗？菱形的判别：四条边都相等的四边形是菱形.∵AB=BC=CD=DA∴四边形ABCD是菱形想一想（2） 如图，当木条AC、BD转动时，什么时候平行四边形变成菱形？菱形的判别对角线互相垂直的平行四边形是菱形∵□ABCD，AC⊥BD∴ □ABCD是菱形菱形的判定：∵AB=BC=CD=DA∴四边形ABCD是菱形∵□ABCDAC⊥BD∴四边形ABCD是菱形∵□ABCDAB=AD∴四边形ABCD是菱形ABCDO合作学习:取一张长方形纸片,对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.(1)(2)(3)1ABCD议一议:(1)剪出的这个图形是哪一种四边形?这是什么四边形?(2)根据折叠, 剪裁的过程,你能说明你的判断的理由吗?运用新知:例:在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于点E,F.
求证:四边形AFCE是菱形.ABF12CDOE证明:∵四边形ABCD是矩形,
∴AE//FC(矩形的定义) ∴∠1=∠2
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF,
∴EO=FO. ∵EF平分AC
∴四边形AFCE是平行四边形(对角线相互平分的四边形是平行四边形).
∵EF⊥AC
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).一展身手:1.已知:在四边形ABCD中,AC=BD,依次是AB,BC,CD,DA的中点.
求证:四边形EFGH是菱形.练习（2）这个菱形的面积是 。 24㎝2（1） 一边长为5cm平行四边形的两条对角线的长分别为6cm和8cm，求证：这个平行四边形为菱形。谈收获定理1.四条边相等的四边形是菱形.定理2.对角线互相垂直的平行四边形是菱形.探究活动:DE,EF是△ABC的两条中位线,我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的形状有什么关系.建议按下列步骤探索:
(1)围成的四边形是否必定是平行四边形?(2)在什么条件下,围成的四边形是菱形?(3)在什么条件下,围成的四边形是矩形?(4)你还能发现其他什么结论吗?布置作业知识运用:1.将菱形ABCD沿AC方向平移至A1B1C1D1,A1D1交CD于点E,A1B1交BC于点F.判断四边形A1FCE是不是菱形,并说明理由.2.在直角坐标系中,点A,B,C,D的坐标依次为
(-1,0),(x,y),(-1,5),(w,z).要使四边形ABCD为菱形,x,y,w,z的值必须满足什么条件?