菱形1[下学期]

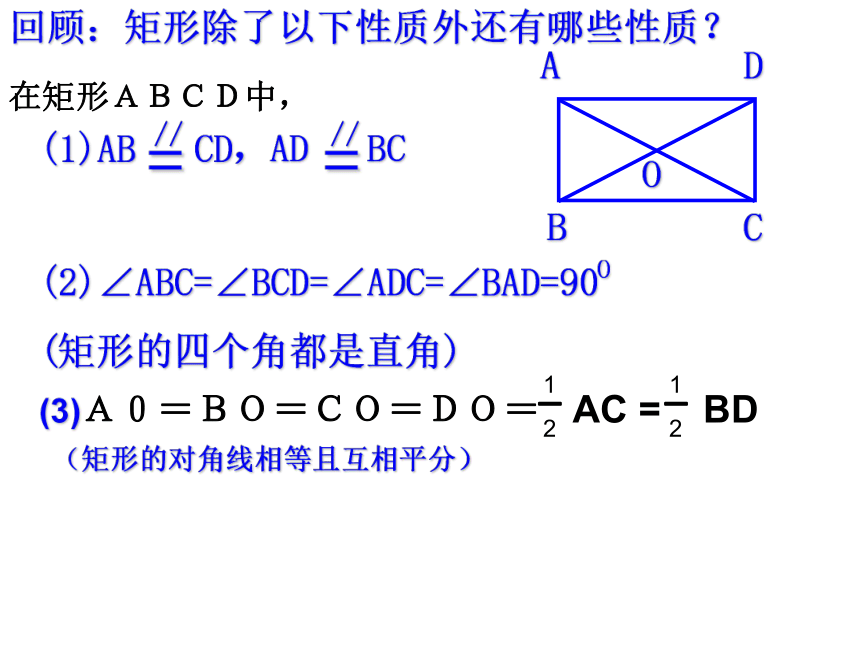
课件25张PPT。6.2(1) 菱形回顾：矩形除了以下性质外还有哪些性质？(2)∠ABC=∠BCD=∠ADC=∠BAD=90O
(矩形的四个角都是直角)
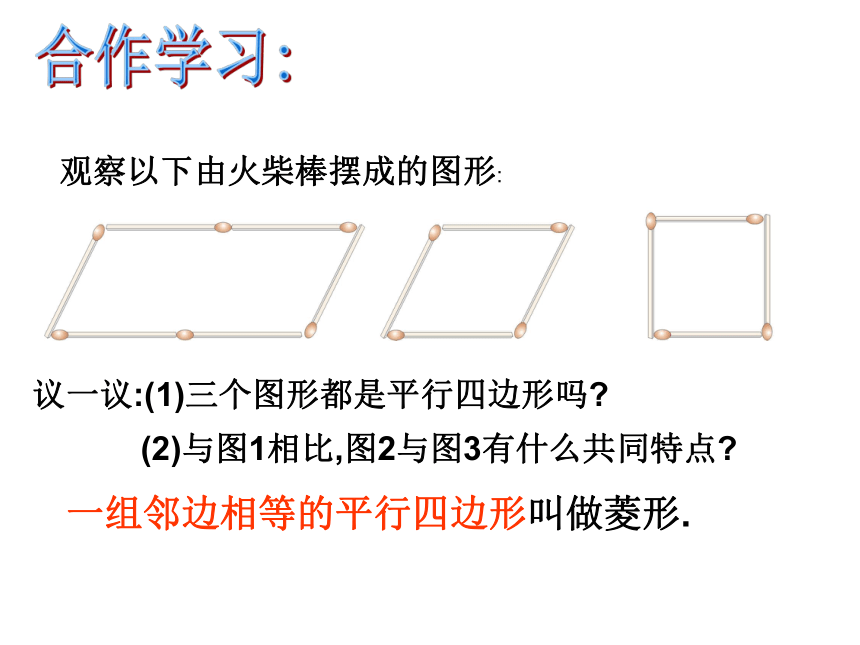
(3)Ａ０＝ＢＯ＝ＣＯ＝ＤＯ＝ AC = BD在矩形ＡＢＣＤ中，（矩形的对角线相等且互相平分）合作学习:观察以下由火柴棒摆成的图形:议一议:(1)三个图形都是平行四边形吗?(2)与图1相比,图2与图3有什么共同特点?
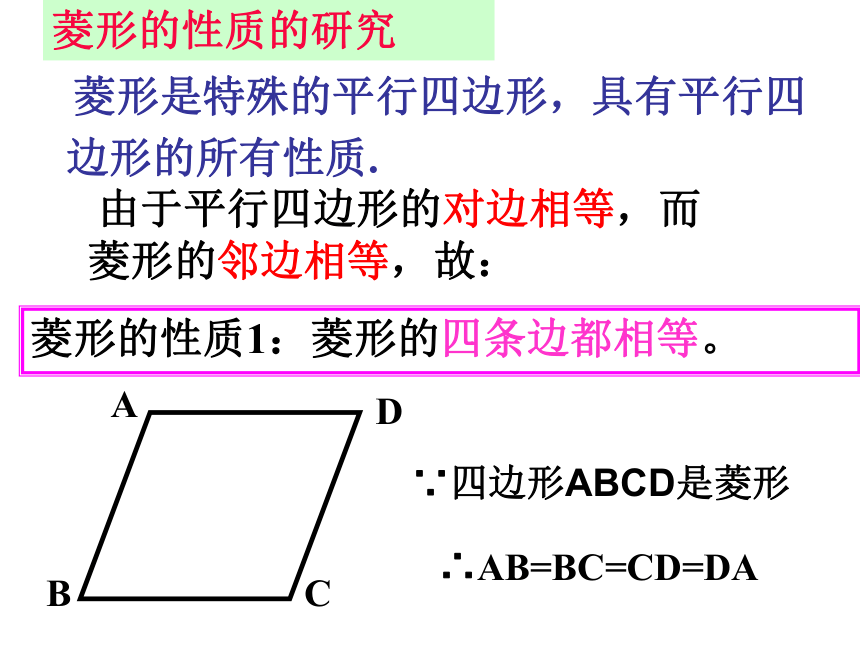
一组邻边相等的平行四边形叫做菱形.菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上. 由于平行四边形的对边相等，而菱形的邻边相等，故：菱形的性质1：菱形的四条边都相等。 菱形是特殊的平行四边形，具有平行四边形的所有性质.菱形的性质的研究∵四边形ABCD是菱形∴AB=BC=CD=DA 菱形的对角线互相垂直,并且每条对角线平 分一组对角.
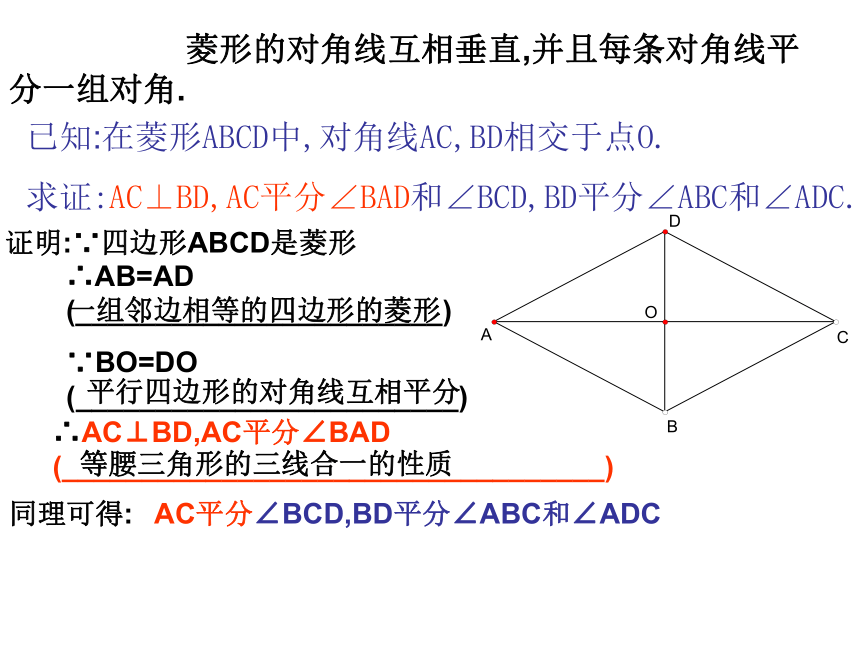
已知:在菱形ABCD中,对角线AC,BD相交于点O.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.定理2证明:∵四边形ABCD是菱形∴AB=AD
(_______________________)一组邻边相等的四边形的菱形∵BO=DO
(________________________)平行四边形的对角线互相平分∴AC⊥BD,AC平分∠BAD
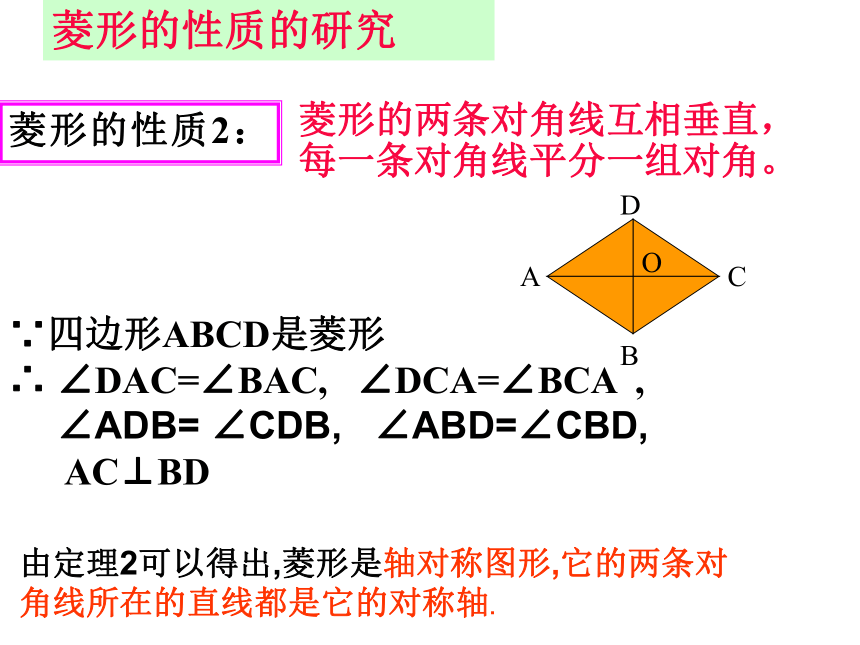
(__________________________________)等腰三角形的三线合一的性质同理可得:AC平分∠BCD,BD平分∠ABC和∠ADC菱形的两条对角线互相垂直，每一条对角线平分一组对角。菱形的性质2：菱形的性质的研究∵四边形ABCD是菱形
∴ ∠DAC=∠BAC, ∠DCA=∠BCA ,
∠ADB= ∠CDB, ∠ABD=∠CBD,
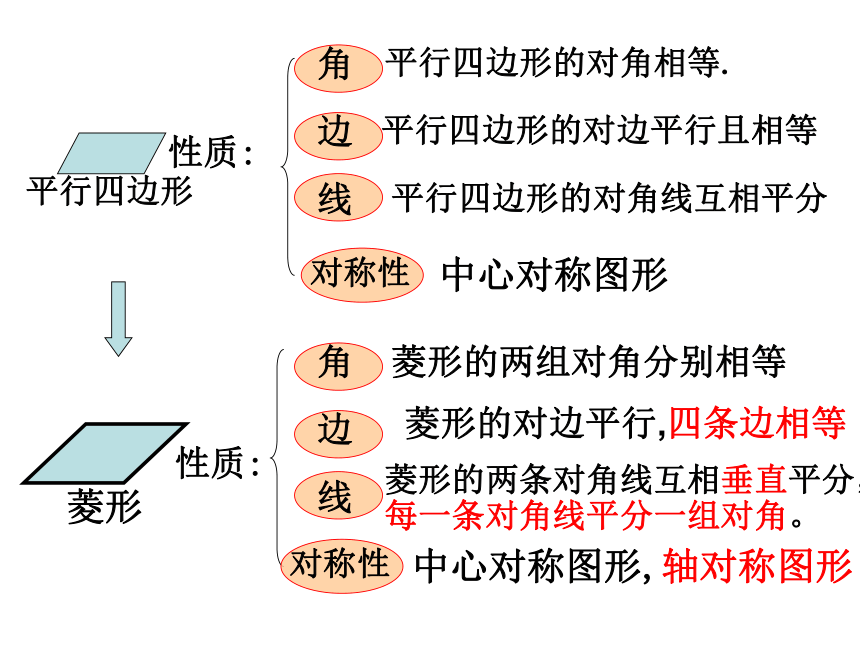
AC⊥BD 由定理2可以得出,菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴.性质:角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分对称性中心对称图形角边线对称性中心对称图形,轴对称图形菱形的对边平行,四条边相等菱形的两组对角分别相等菱形的两条对角线互相垂直平分，每一条对角线平分一组对角。相等的线段：相等的角：等腰三角形有：直角三角形有：已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD , ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 , ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOAABCDO12345678..例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.解:∵四边形ABCD是菱形,∴∠BAD=2 ∠BAC=2×30°= 60°∴⊿ABD是等边三角形.∴由勾股定理,得AO=30°∴AB=CD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)∴ AB=BD=6(有一个角是60度的等腰三角形的等边三角形)∵ AC⊥BD(菱形的对角线互相垂直)又∵OB=OD= BD= ×6=3(平行四边形的对角线互相平分)∴菱形的边长为AB=BC=CD=DA=6(菱形的四条边相等)知识运用:1.菱形具有而矩形不一定有的性质是( )
(A)对角线互相平分 (B)四条边都相等
(C)对角相等 (D)邻角互补B[作业题3］如图四边形ＡＢＣＤ和四边形ＡＥＣＦ都是
菱形，点Ｅ，Ｆ在ＢＤ上，已知∠ＢAD=100°,
∠EAF=60°,则∠ABD=______°, ∠BAE=______°∵四边形ＡＥＣＦ是菱形∴AB=AD(___________________)菱形的四条边相等∴∠ABD=∠ADB=40度∵ ∠ABD+∠ADB=180°- ∠ＢAD=180°-100°=80°
(三角形的内角和等于180度)40连结AC∵四边形ＡＢＣＤ和四边形ＡＥＣＦ都是菱形∴∠BAC=∠CAD= ∠BAD=50度12∠1=∠2= ∠EAF=30度(___________________________)菱形的对角线平分每一组对角∴∠BAE= ∠BAC - ∠1 =20度20知识运用:2.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F.
求证:AE=AF.【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积：S菱形=底×高=对角线乘积的一半⒉菱形的两条对角线长分别为6cm和8cm，则菱形的边长是（ ）A.10cm B.7cm
C. 5cm D.4cm34C3.上题中菱形的周长是____________, 面积是_________高是____20cm24cm24,已知菱形的一条对角线为16一条边为10求菱形的面积.5.菱形ABCD的周长为16，相邻两角的度数比为1：2．⑴求菱形ABCD的对角线的长；⑵求菱形ABCD的面积．两组对边
分别平行矩形有一个角是直角菱形有一组邻边相等谈收获一组邻边相等的平行四边形叫做菱形.定理1.菱形的四条边都相等.定理2.菱形的对角线相互垂直,
并且每条对角线平分一组对角菱形是轴对称图形,它的两条对角线所在的直线
都是它的对称轴.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F且E,F分别是BC,CD的中点,求菱形各个内角的度数.
6.已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AB=1。
求（1）∠ABC的度数；
（2）对角线BD 、 AC的长；
（3）菱形ABCD的面积。课后练习1,菱形具有而矩形不一定具有的特性是:两条对角线每一条对角线_____;各边_____;
2.菱形的周长是44CM则它的边长是_____.
3,菱形的两个邻角之比为1:2,周长为4A,则短对角线的长为____.
4,下列图形中不是中心对称图形的是( )
A菱形 B平行四边形 C等边三角形 D圆
5,从菱形的钝角顶点向对边作垂线,如果垂线平分对边,则菱形的四个角的度数为( )知识拓展:5.在菱形ABCD中,CE⊥AB于E,已知∠BCE=30°,CE=3cm.求菱形ACD的周长和面积.4.已知:在菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.求证:(1) △ABE≌△ADF;
(2) ∠AEF=∠AFE布置作业