6.1矩形(1)[下学期]

课件17张PPT。矩形 我们生活中充满了矩形和正方形这两种几何图形，教室里的黑板，门窗，课桌的桌面，信封明信片等都是矩形或正方形的形状，而你是否了解这两种几何图形的性质呢？
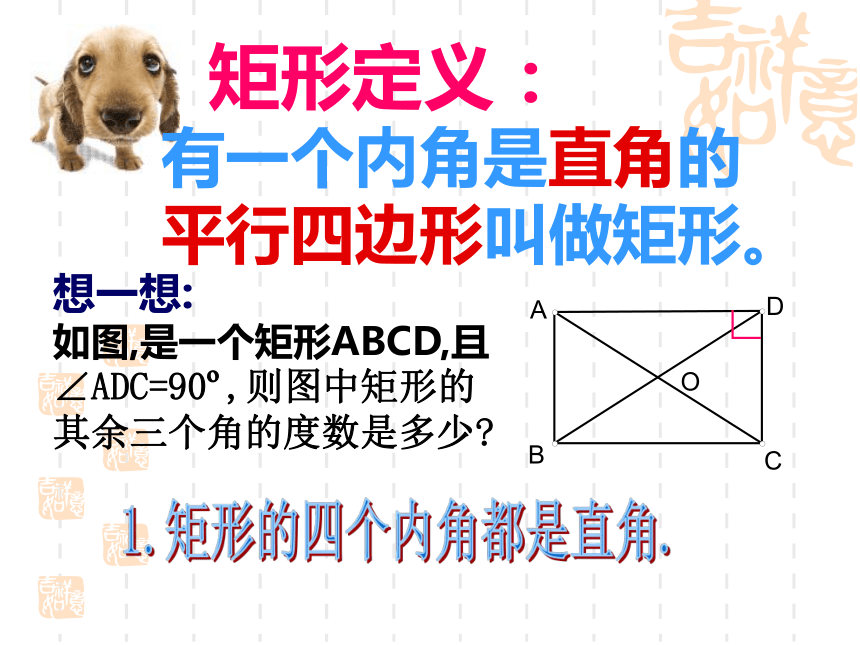
这节课我们一起来学习一下吧！我们先由矩形开始吧！活动一：思考讨论1:矩形是平行四边形吗？2:平行四边形经过怎样的 变化就成为了矩形呢？矩形定义：有一个内角是直角的
平行四边形叫做矩形。∟想一想:
如图,是一个矩形ABCD,且
∠ADC=90o,则图中矩形的
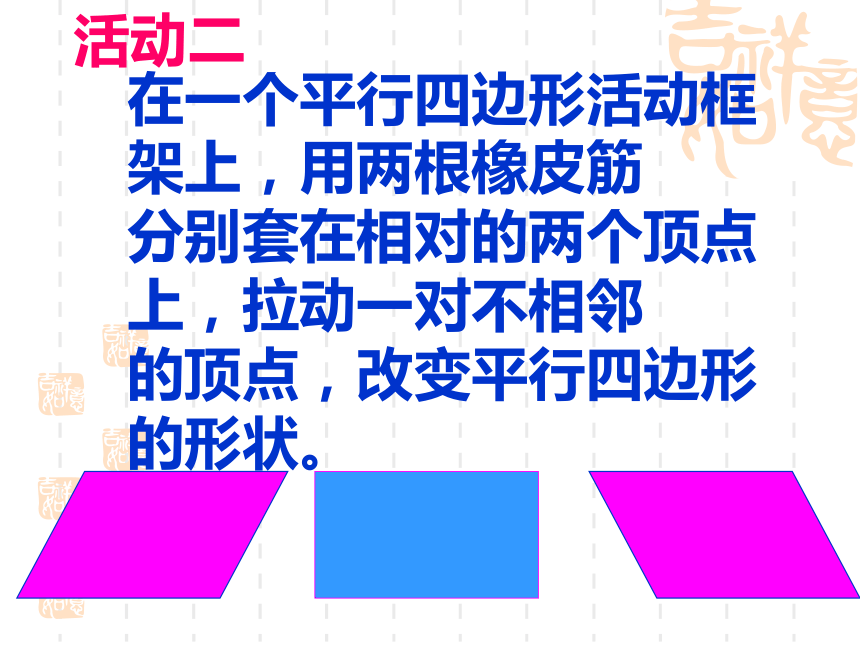
其余三个角的度数是多少?1.矩形的四个内角都是直角.在一个平行四边形活动框架上，用两根橡皮筋
分别套在相对的两个顶点上，拉动一对不相邻
的顶点，改变平行四边形的形状。活动二（1）随着∠a的变化,两条对角线的长度
怎样变化的？（2)当∠a是锐角时，两条对角线的长度有什么关系？当∠a是钝角时呢？
（3)当∠a是直角时，平行四边形变成
矩形，此时两条对角线的长度有什么
关系？随着∠a的变化，一条对角线在变长，一条在变短。当∠a是锐角时，过∠a的顶点的那条对角线
比另一条长；当∠a是钝角时，过∠a的顶点
的那条对角线比另一条短两条对角线相等矩形性质：2.矩形的对角线相等.1.矩形的四个内角都是直角.你觉得矩形还有其他什么性质吗?3.矩形具有平行四边形所有的性质.4.矩形既是轴对称图形,
又是中心对称图形.例1: 如图,矩形ABCD被两条对角线分成四个小
三角形,如果四个小三角形的周长的和是86
Cm,对角线长是13cm,那么矩形的周长是多少?ABCDO活动三：想一想结论：对角线相等的平行四边形是矩形对角线相等的平行四边形是怎样的四边形？识别方法一：
对角线相等的平行四边形是矩形在平行四边形ABCD中，
如果AC=BD
那么四边形ABCD是矩形想一想：
对角线相等且互相平分的四边形是矩形吗？识别方法二：
对角线相等且互相平分的四边形是矩形大显身手：已知：如图，在平行四边形ABCD中，AC、BD 相交于点o， △ AOB是等边三角形。求： ∠BAD的度数解：∵ △AOB是等边三角形∴OA=OB∵四边形ABCD是平行四边形∴AC=2OA,BD=2BO∴AC=BD∴平行四边形ABCD是矩形∴∠BAD＝90°。答： ∠BAD＝90°。(对角线相等的平行
四边形是矩形)例2:已知在四边形ABCD中, ∠A=∠B=∠C=90o,试问
四边形ABCD是矩形吗?若是,请说明理由.ABCD识别方法三：
三个角是直角的四边形是矩形.练习1、矩形具有而平行四边形不具有的性质是（ ）
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
2、下面说法中正确的是 （ ）
A 有一个角是直角的四边形是矩形
B 两条对角线相等的四边形是矩形
C 两条对角线互相垂直的四边形是矩形
D 四个角都是直角的四边形是矩形AD自我诊断1、能够判断一个四边形是矩形的条件是（ ）
A 对角线相等 B 对角线垂直
C对角线互相平分且相等 D对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm，则它的对角线长是 cm
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线，则四边形ABCD是（ ）
A 菱形 B 平行四边形
C 矩形 D 不能确定

A5C归纳小结:
1.矩形的定义:
有一角是直角的平行四边形是矩形.2.矩形的特征:
(1)四个角都是直角;
(2)对角线相等.
(3)具有平行四边形的所有特征;
(4)既是轴对称图形,又是中心对称图形.3.矩形的识别方法:
(1)有一角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是直角;
(3)对角线相等的平行四边形是矩形;
(4)对角线相等且互相平分的四边形是矩形.作业：1、如图，矩形ABCD的对角线AC、BD相交于O，∠BOC=2 ∠ AOB，若AC=6cm,试求AB的长。
2、如图，O是菱形ABCD对角线的交点，作DE∥AC，CE∥BD，DE、CE交于点E，四边形CEDO是矩形吗？说出你的理由。