6.1矩形（1）[下学期]

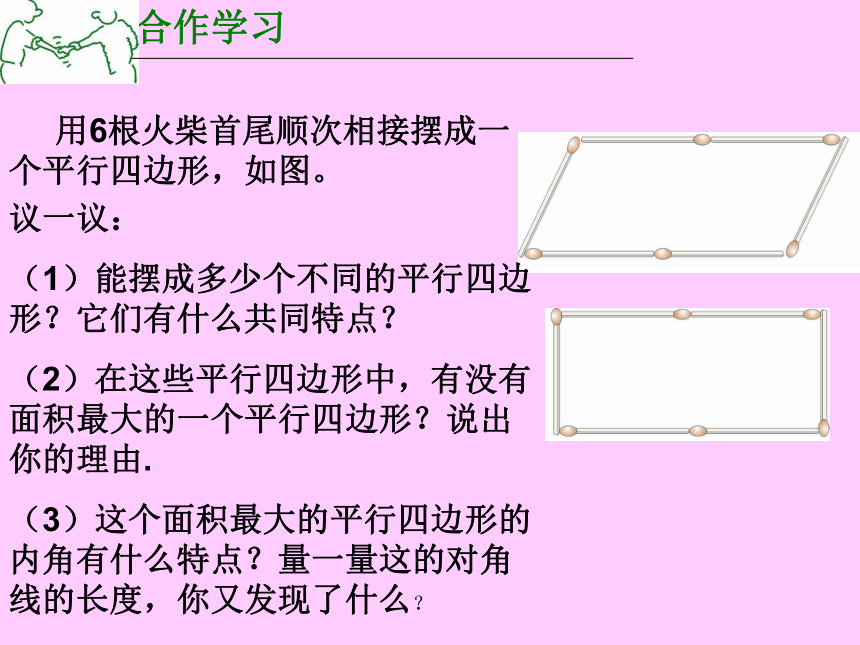
课件10张PPT。6.1 矩 形 1合作学习 用6根火柴首尾顺次相接摆成一个平行四边形，如图。议一议：
（1）能摆成多少个不同的平行四边形？它们有什么共同特点？
（2）在这些平行四边形中，有没有面积最大的一个平行四边形？说出你的理由.
（3）这个面积最大的平行四边形的内角有什么特点？量一量这的对角线的长度，你又发现了什么？概念：有一个角是直角的平行四边形叫做矩形
（rectangle)小学里学过的长方形、正方形都是矩形. 在我们的日常生活中和生产实际中，矩形有着广泛的应用. 矩形是特殊的平行四边形，所以它不但具有一般平行四边形的性质，而且还具有一些特殊的性质。矩形的四个角都是直角.矩形的对角线相等.定理1定理2已知：如图，AC，BD是矩形ABCD的对角线.求证：AC＝BD.证明　在矩形ABCD中，∵AB＝CD（平行四边形的对边相等）∠ABC＝∠DCB＝Rt∠(矩形的四个角都是直角)∴Rt△ABC≌Rt△DCB.∴AC＝BD. 矩形是特殊的平行四边形，所以它不但具有一般平行四边形的性质，而且还具有一些特殊的性质。矩形的四个角都是直角.矩形的对角线相等.定理1定理2思考：对角线AC、BD相交于点O，图中有多少个等腰三角形？有多少对全等三角形？O　　例1　已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠AOD＝120o，AB＝4cm.
（1）判断△AOB的形状；
（2）求矩形对角线的长.解　（1）∵四边形ABCD是矩形.∴AC＝BD（矩形的对角线相等）∵OA＝OC＝　　AC，OB＝OD＝　　BD（平行四边形的对角线互相平分）∴OA＝OB＝OC＝OD.∵∠AOD＝120o，∴∠AOB＝60o∴△AOB是等边三角形.（2）∵AB＝4cm，
∴AC＝BD＝2AB＝8cm.即矩形对角线的长为8cm.ABCDl1l2矩形既是中心对称图形，又是轴对称图形。课内练习：1.如图，在矩形ABCD中，E，F分别是AB，CD的中点.求证：四边形AEFD是矩形.2：已知:如图,过矩形ABCD的顶点作CE//BD，交AB的延长线于E。求证：∠CAE=∠CEA本节课你学到什么？