三角形中内接矩形[上学期]

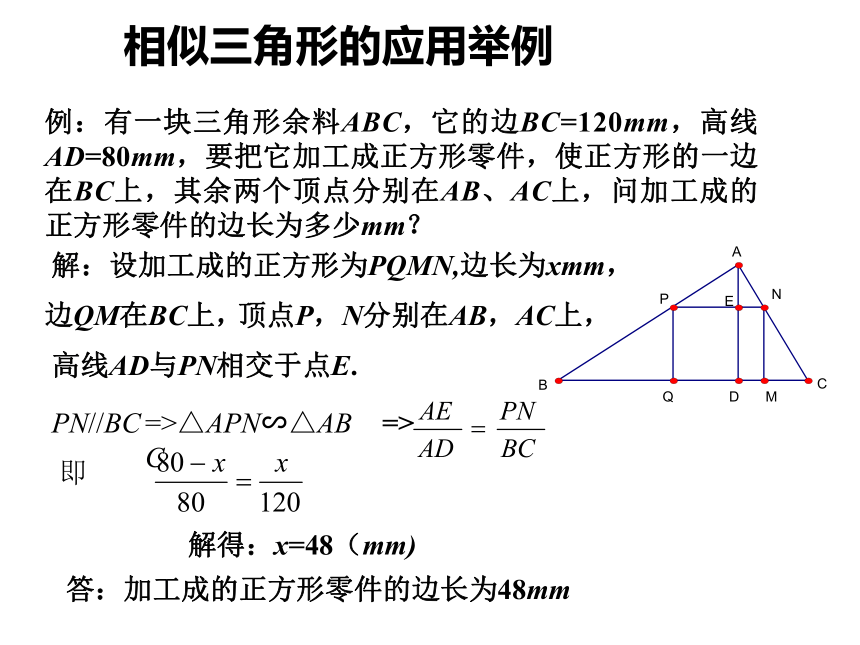
课件7张PPT。三角形中的内接矩形相似三角形的应用举例例：有一块三角形余料ABC，它的边BC=120mm，高线AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，问加工成的正方形零件的边长为多少mm？
高线AD与PN相交于点E.
PN//BC=>△APN∽△ABC即
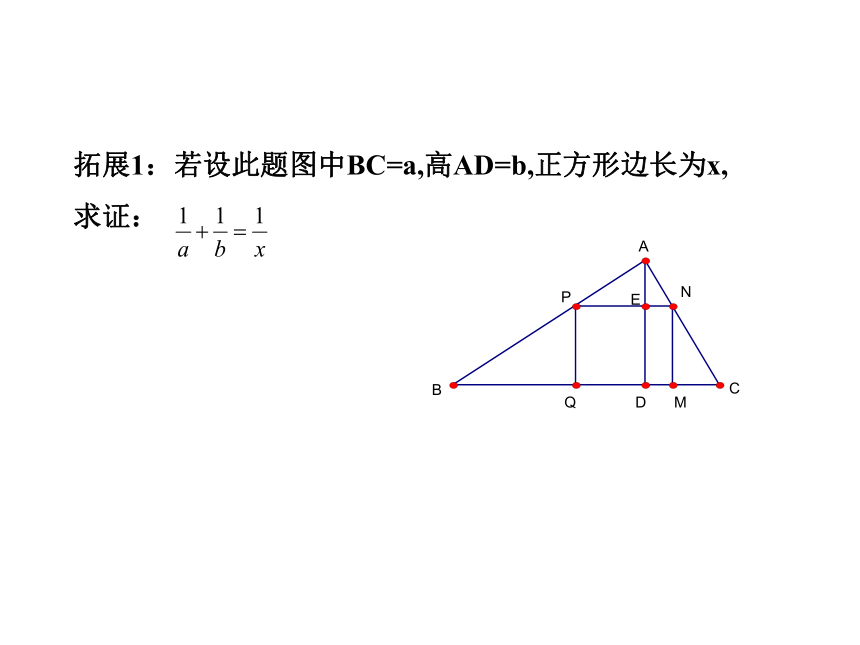
解得：x=48（mm)答：加工成的正方形零件的边长为48mm=>解：设加工成的正方形为PQMN,边长为xmm，边QM在BC上，顶点P，N分别在AB，AC上，拓展1：若设此题图中BC=a,高AD=b,正方形边长为x,
求证： 拓展2：若要把它加工成矩形零件，使矩形的一边QM在BC上，其余两个顶点P、N分别在AB，AC上，设AD与矩形PQMN的PN边相交于E点，问当AE为多少时？矩形PQMN的面积最大，最大面积为多少？
拓展3：划线部分若改成问是否存在这样的两个矩形，使这两个矩形的面积之和等于此三角形的面积？若存在，请指出这两个矩形，若不存在，请说明理由。解：设AE为xmm，矩形PQMN的面积为s mm2 PN//BC =>△APN∽△ABC<=即 PN= 1.5x
∴ S=PN·ED =1.5x（80 - x） = -1.5x2+120x
∴ S= - 1.5（x-40）2+2400
∵-1.5＜0 ∴S有最大值 ,当 x=40(在0＜x＜80范围内）时， S最大值=2400
即当AE为40mm时，矩形PQMN的面积最大，最大面积为2400mm2
(0＜x＜80)
x:80 = PN:120 拓展4：如图，有一块三角形余料ABC，它的边BC=120mm，高线AD=80mm，要把它加工成矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，当矩形PQMN与△ABC的面积之比为3∶8时，求矩形PQMN的周长.
解：由拓展（2）可知: 矩形面积S= - x2+120x（其中x是AE的长）， S△ABC = BC·AD= ×120×80=4800
∴得：x2-80x+120=0
∴ （x-20）（x-60）=0∴x1=20，x2=60
当x1=20时， 即AE=20， ED=PQ=80-20=60,
又由拓展（1）可知PN=1.5x=30
∴ 矩形PQMN周长为=2（PQ+PN）=180（mm）当x=60时， 即AE=60，ED=PQ=80-60=20,
同理可知PN=1.5x=90
∴矩形PQMN的周长为2（PQ+PN）=220（mm）
答：矩形PQMN的周长为180 mm或220 mm。
拓展5：已知△ABC，若AB=2 ，BC=12，AC=10，要把它加工成正方形零件，若正方形一边分别在AB、AC、BC上，其余两顶点在另两条边上，问在哪一边上截得的正方形面积最大？
(1)(2)拓展6：已知△ABC，若AB=2 ，BC=12，AC=10，要把它加工成矩形零件，若矩形一边分别在AB、AC、BC上，其余两顶点在另两条边上，问在哪一边上截得最大面积的矩形？
(1)(2)