1.3解直角三角形应用举例[上学期]
图片预览




文档简介
课件14张PPT。 解直角三角形
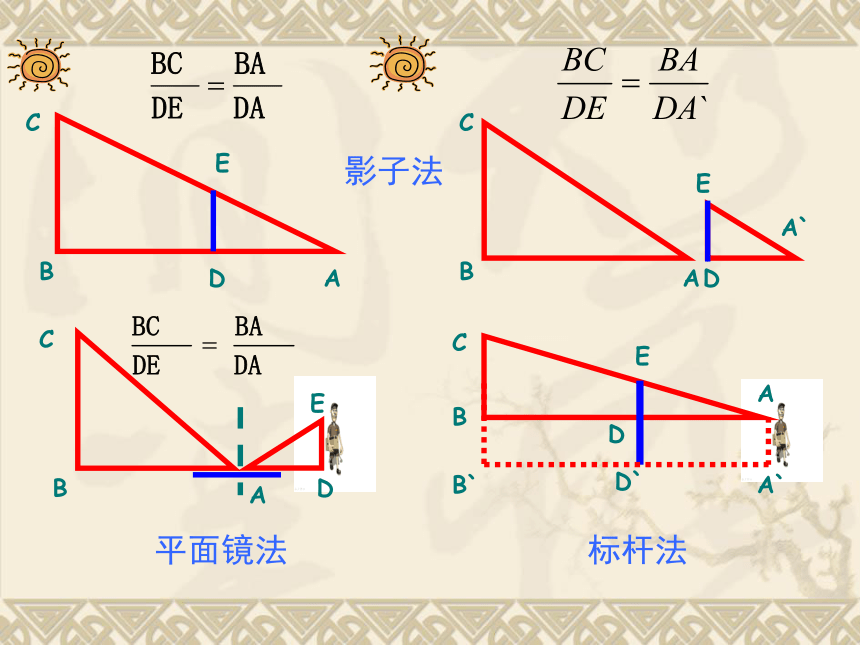
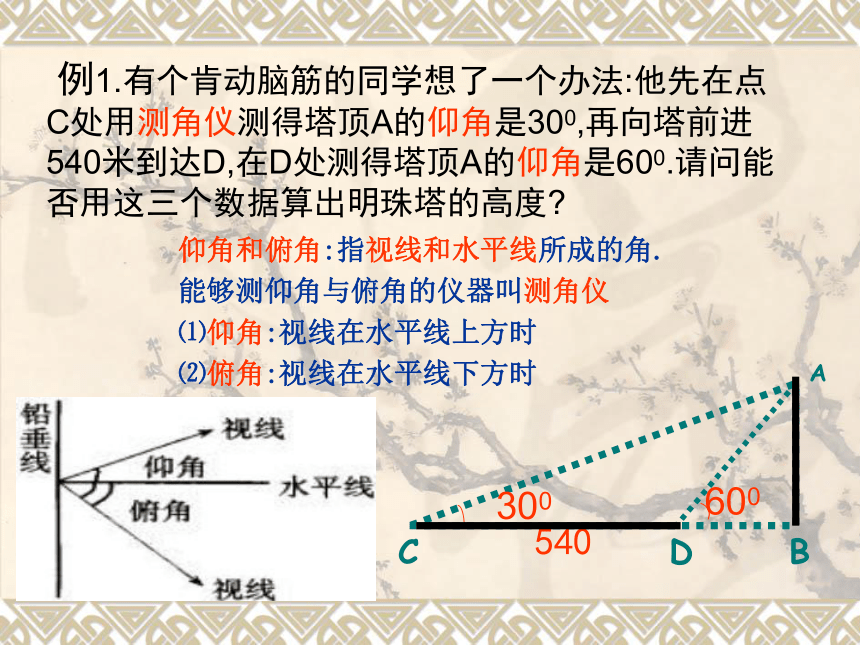
的应用举例(二) 瓜沥一中 龙志祥ABCDEABCDEA`B`D`EABCDAEA`BCD影子法平面镜法标杆法 例1.有个肯动脑筋的同学想了一个办法:他先在点C处用测角仪测得塔顶A的仰角是300,再向塔前进540米到达D,在D处测得塔顶A的仰角是600.请问能否用这三个数据算出明珠塔的高度?
CABD300600540⌒仰角和俯角:指视线和水平线所成的角.
能够测仰角与俯角的仪器叫测角仪
⑴仰角:视线在水平线上方时
⑵俯角:视线在水平线下方时
解: 在Rt△ADB中,
BD= ABcot∠ADB=ABcot60°. 在Rt△ACB中,
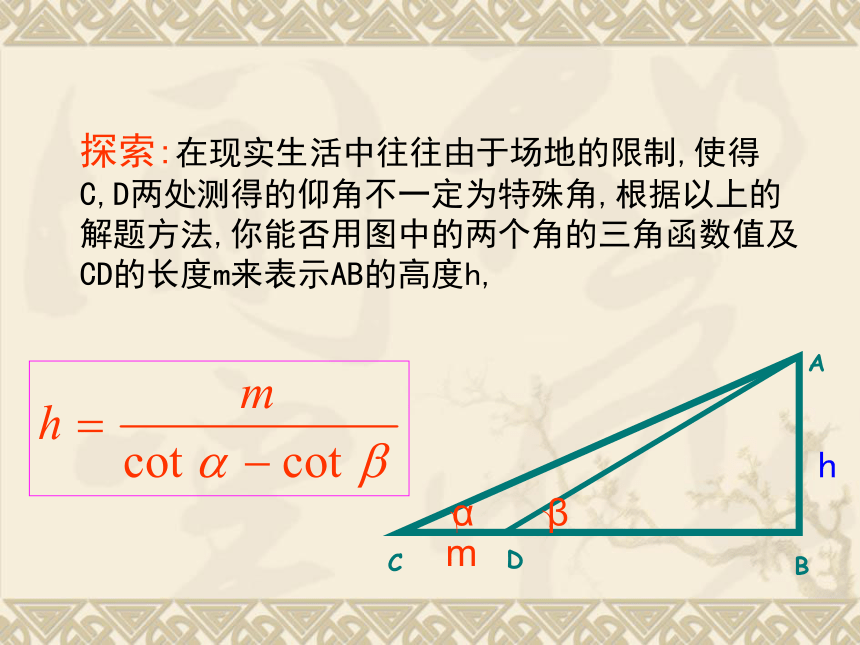
BC= ABcot∠ACB=ABcot30°. ∵ BC -BD=CD= 540m,即 ABcot30o - ABcot60o = 540,∴CDBA﹚﹚60°30°540m答:塔高为 m?探索:在现实生活中往往由于场地的限制,使得C,D两处测得的仰角不一定为特殊角,根据以上的解题方法,你能否用图中的两个角的三角函数值及CD的长度m来表示AB的高度h, 求山高或建筑物的高;测量河的宽度或物体的长度;航行航海问题等.解决这类问题的关键是先画出测量示意图,把实际问题转化为数学问题,利用直角三角形中角、边之间的数量关系求出所要求的距离或角度. 应用解直角三角形知识解应用题时,可按以下思维过程进行:
(1)画出测量示意图;
(2)寻找直角三角形,若找不到,可构造;
(3) 解直角三角形,若不可直接求解,利用题中的数 量关系,设x求解.方法归纳例2.已知在△ABC中,∠A=600,AB=7,AC=3,求△ABC的面积.探索:在△ABC中,若锐角∠C=α,CB=a,AC=b, 根据以上的解题方法,猜想△ABC的面积S的表达式,并给以证明.3×sin60037600b×sinαD练习
求证: ABCD的面积 S = AB ·BC ·sinB(∠B为锐角)。AB×sinB例3.已知在△ABC中,∠A为锐角,sinA= AB+AC=6cm,设AC=xcm,△ABC的面积为ycm2.
(1)求关于的函数关系式和自变量的取值范围:
(2)何时的面积最大,最大面积是多少? 解:
(1) ∵AB+AC=6cm,AC=xcm
∴AB=(6-x)cm2
∵
∴
自变量的取值范围是0<x<6(2)
当x=3(属于0<x<6)时△ABC的面积最大为3.
答:当AB=AC=3cm时, △ABC的面积最大,最大面积为3cm2
x6-x⌒sinA=例4.如图, △ABC的面积为1,A`.B`.C`分别是BC,CA,AB上的点,且
(0<x≤1).设△AB`C`的面积为y.
求y关于x的函数关系式;(2) 探究△A`B`C`面积是否有最小值. 4.应用解直角三角形知识把实际问题转化为数学问题而加以解决.小结再见
的应用举例(二) 瓜沥一中 龙志祥ABCDEABCDEA`B`D`EABCDAEA`BCD影子法平面镜法标杆法 例1.有个肯动脑筋的同学想了一个办法:他先在点C处用测角仪测得塔顶A的仰角是300,再向塔前进540米到达D,在D处测得塔顶A的仰角是600.请问能否用这三个数据算出明珠塔的高度?
CABD300600540⌒仰角和俯角:指视线和水平线所成的角.
能够测仰角与俯角的仪器叫测角仪
⑴仰角:视线在水平线上方时
⑵俯角:视线在水平线下方时
解: 在Rt△ADB中,
BD= ABcot∠ADB=ABcot60°. 在Rt△ACB中,
BC= ABcot∠ACB=ABcot30°. ∵ BC -BD=CD= 540m,即 ABcot30o - ABcot60o = 540,∴CDBA﹚﹚60°30°540m答:塔高为 m?探索:在现实生活中往往由于场地的限制,使得C,D两处测得的仰角不一定为特殊角,根据以上的解题方法,你能否用图中的两个角的三角函数值及CD的长度m来表示AB的高度h, 求山高或建筑物的高;测量河的宽度或物体的长度;航行航海问题等.解决这类问题的关键是先画出测量示意图,把实际问题转化为数学问题,利用直角三角形中角、边之间的数量关系求出所要求的距离或角度. 应用解直角三角形知识解应用题时,可按以下思维过程进行:
(1)画出测量示意图;
(2)寻找直角三角形,若找不到,可构造;
(3) 解直角三角形,若不可直接求解,利用题中的数 量关系,设x求解.方法归纳例2.已知在△ABC中,∠A=600,AB=7,AC=3,求△ABC的面积.探索:在△ABC中,若锐角∠C=α,CB=a,AC=b, 根据以上的解题方法,猜想△ABC的面积S的表达式,并给以证明.3×sin60037600b×sinαD练习
求证: ABCD的面积 S = AB ·BC ·sinB(∠B为锐角)。AB×sinB例3.已知在△ABC中,∠A为锐角,sinA= AB+AC=6cm,设AC=xcm,△ABC的面积为ycm2.
(1)求关于的函数关系式和自变量的取值范围:
(2)何时的面积最大,最大面积是多少? 解:
(1) ∵AB+AC=6cm,AC=xcm
∴AB=(6-x)cm2
∵
∴
自变量的取值范围是0<x<6(2)
当x=3(属于0<x<6)时△ABC的面积最大为3.
答:当AB=AC=3cm时, △ABC的面积最大,最大面积为3cm2
x6-x⌒sinA=例4.如图, △ABC的面积为1,A`.B`.C`分别是BC,CA,AB上的点,且
(0<x≤1).设△AB`C`的面积为y.
求y关于x的函数关系式;(2) 探究△A`B`C`面积是否有最小值. 4.应用解直角三角形知识把实际问题转化为数学问题而加以解决.小结再见
