1.3解直角三角形举例(一)[下学期]
文档属性
| 名称 | 1.3解直角三角形举例(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 266.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-18 00:00:00 | ||
图片预览


文档简介
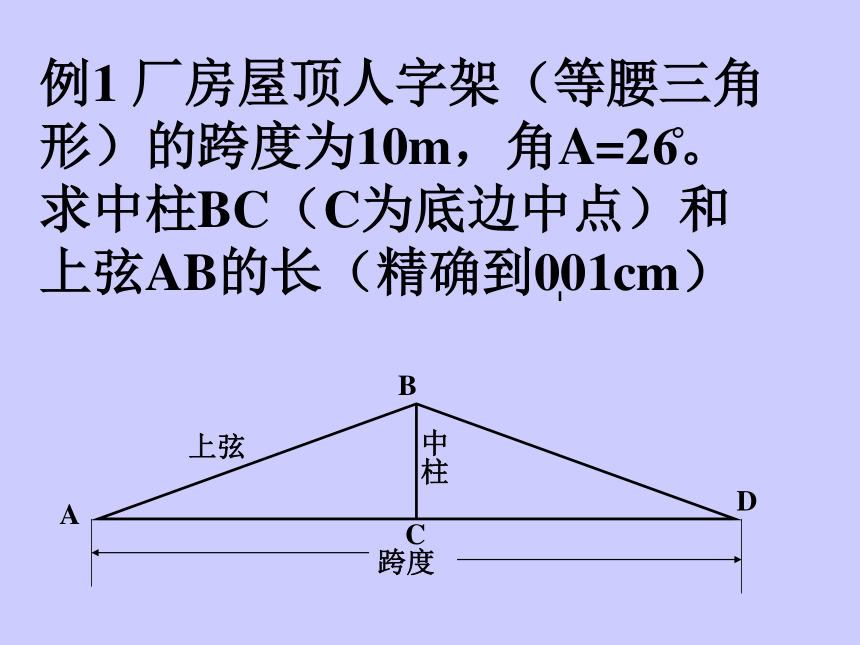
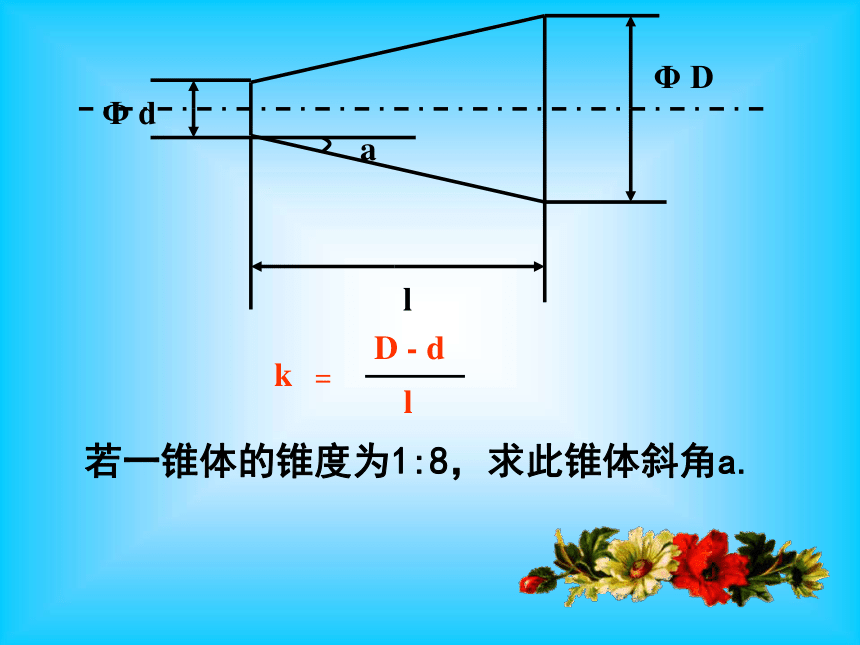
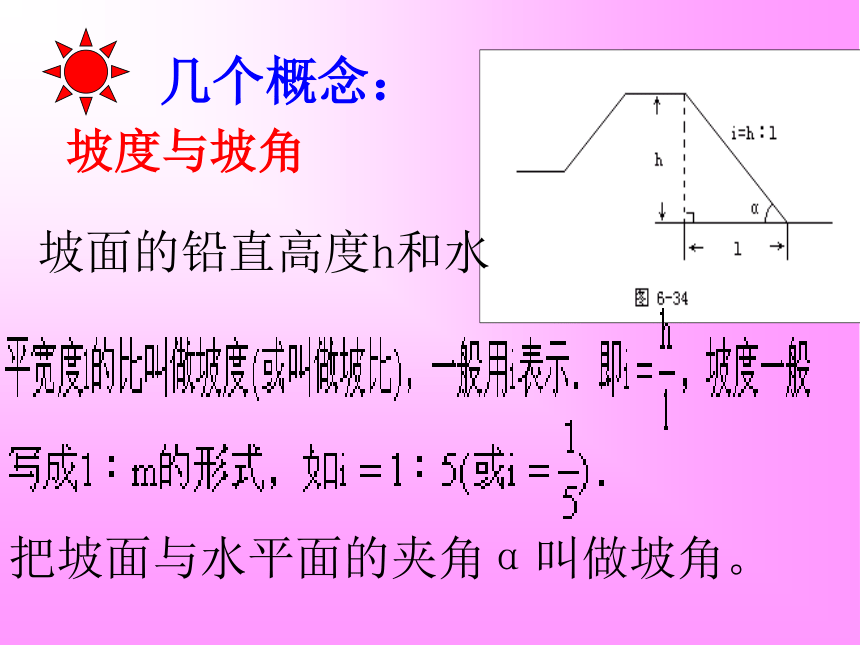
课件14张PPT。解直角三角形应用例1 厂房屋顶人字架(等腰三角形)的跨度为10m,角A=26?。求中柱BC(C为底边中点)和上弦AB的长(精确到0?01cm)跨度ABCD上弦中柱若一锥体的锥度为1:8,求此锥体斜角a.几个概念:坡度与坡角 坡面的铅直高度h和水
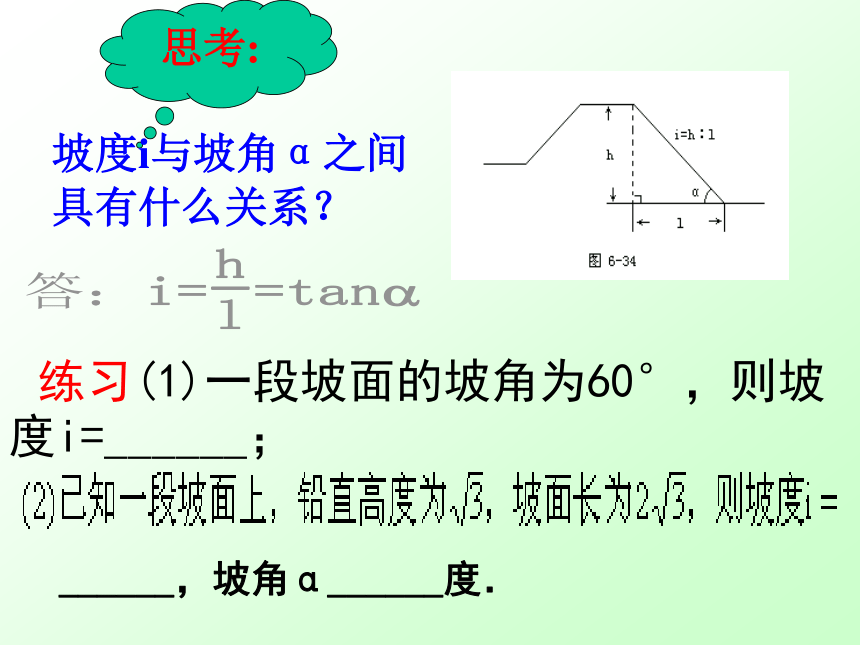
把坡面与水平面的夹角α叫做坡角。 思考:坡度i与坡角α之间
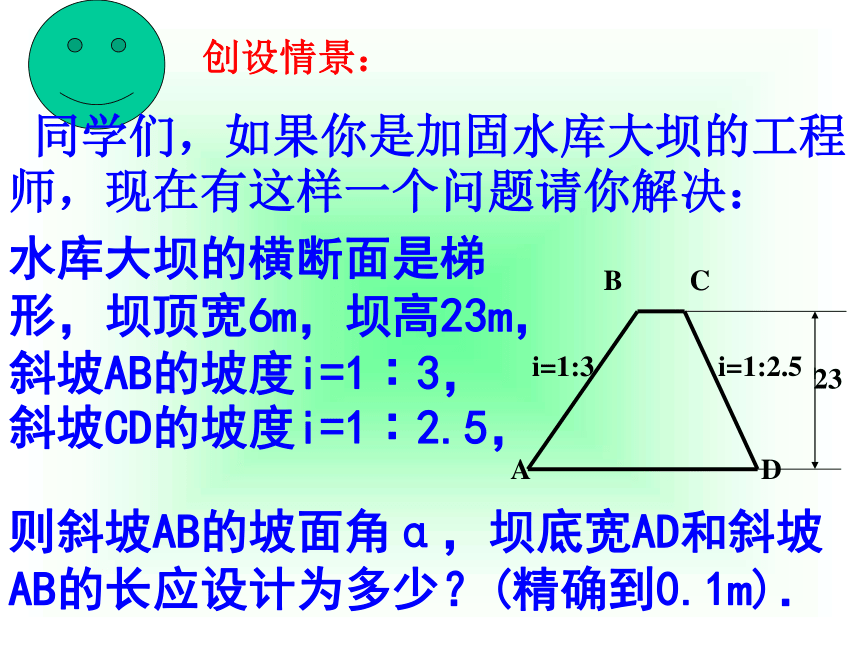
具有什么关系? 练习(1)一段坡面的坡角为60°,则坡度i=______;______,坡角α______度.创设情景: 同学们,如果你是加固水库大坝的工程师,现在有这样一个问题请你解决:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,BCi=1:2.5i=1:3则斜坡AB的坡面角α,坝底宽AD和斜坡AB的长应设计为多少?(精确到0.1m).
1、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m .2、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示).练一练B在解直角三角形中,经常接触的名称:(返回)小结1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系.2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300和450的三角板去度量旗杆的高度。若王同学分别在点C、点D处将旗杆上绳子分别拉成,如图量出CD=8米,你能求出旗杆AB的长吗?测一测ABC8m450600D 横截面为等腰梯形的水库大坝,坝顶宽6m,坝高10m,斜坡AB的坡度i=1:2,为了提高大坝的储水能力,在坝顶宽度和斜坡坡度不变的情况下,加固一条长50m的大坝,需要多少土方?算一算再见
把坡面与水平面的夹角α叫做坡角。 思考:坡度i与坡角α之间
具有什么关系? 练习(1)一段坡面的坡角为60°,则坡度i=______;______,坡角α______度.创设情景: 同学们,如果你是加固水库大坝的工程师,现在有这样一个问题请你解决:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,BCi=1:2.5i=1:3则斜坡AB的坡面角α,坝底宽AD和斜坡AB的长应设计为多少?(精确到0.1m).
1、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m .2、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示).练一练B在解直角三角形中,经常接触的名称:(返回)小结1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系.2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300和450的三角板去度量旗杆的高度。若王同学分别在点C、点D处将旗杆上绳子分别拉成,如图量出CD=8米,你能求出旗杆AB的长吗?测一测ABC8m450600D 横截面为等腰梯形的水库大坝,坝顶宽6m,坝高10m,斜坡AB的坡度i=1:2,为了提高大坝的储水能力,在坝顶宽度和斜坡坡度不变的情况下,加固一条长50m的大坝,需要多少土方?算一算再见
