1.2有关三角函数的计算(2)[上学期]
文档属性
| 名称 | 1.2有关三角函数的计算(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 116.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-17 20:28:00 | ||
图片预览



文档简介
课件12张PPT。1.2 有关三角函数的计算第二课时上节课 ,我们已经知道:已知任意一个
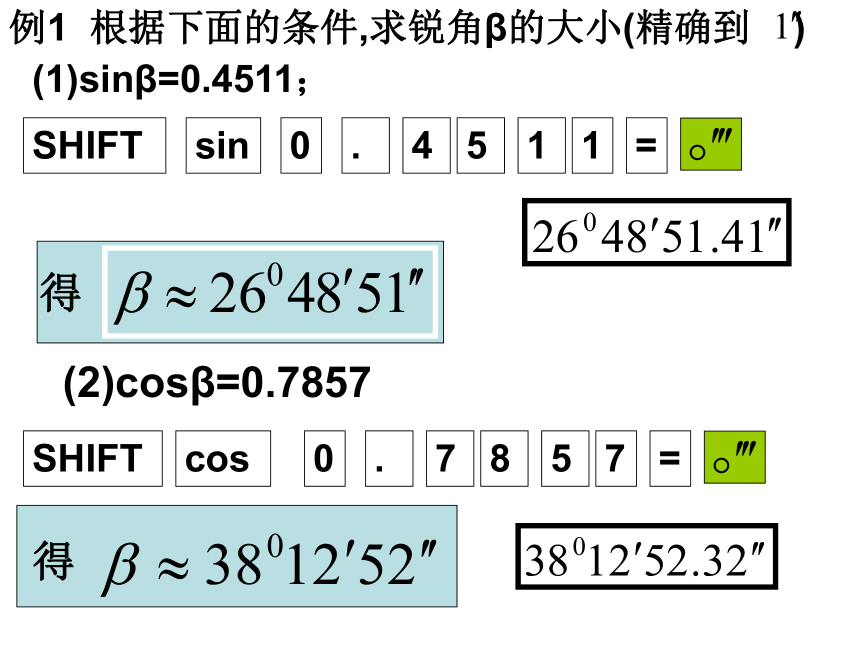
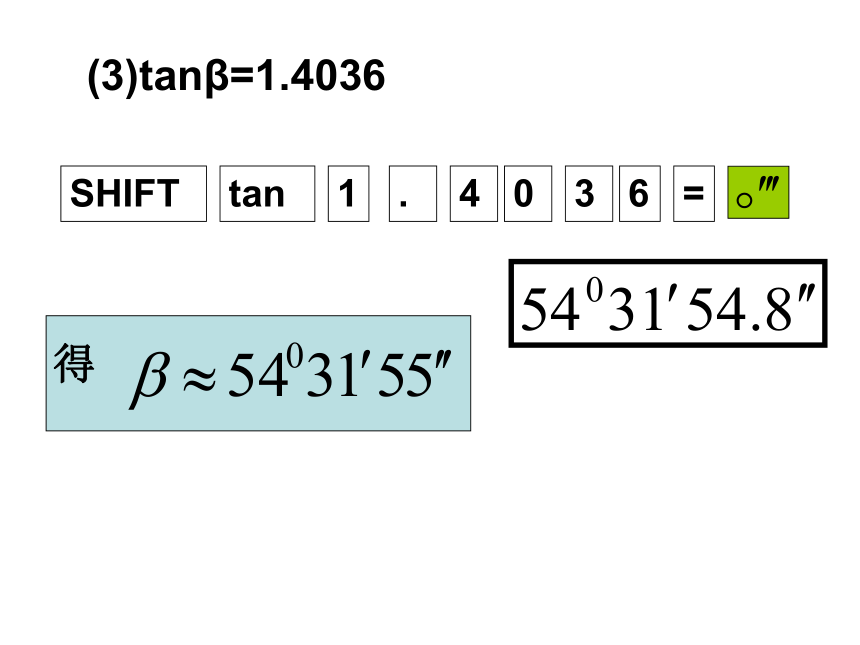
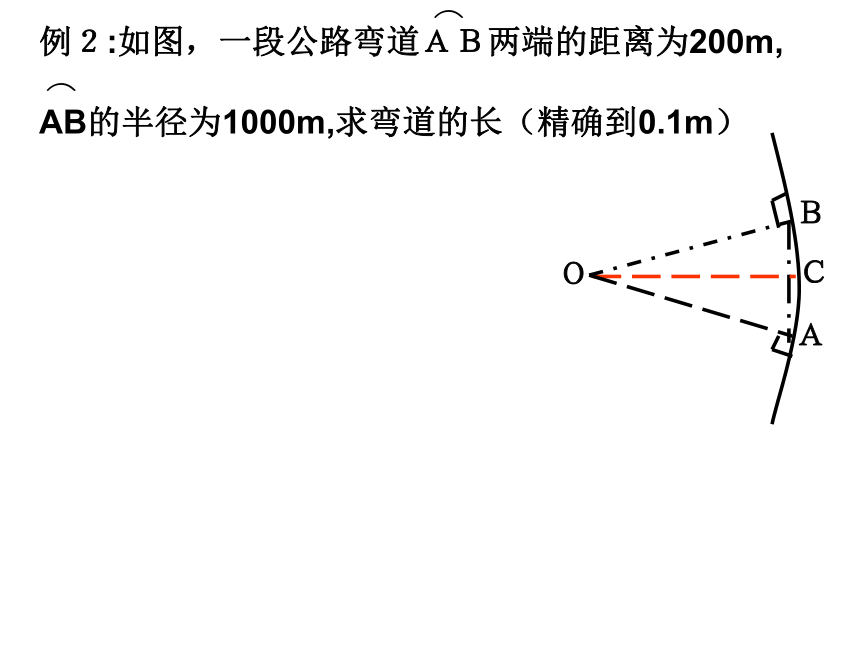
锐角,用计算器都可以求出它的函数值.反之,已知三角函数值能否求出相应的角度?例如,已知sinα=0.2974,求锐角α.按键顺序如下:17.30150783即α=17.30150783例1 根据下面的条件,求锐角β的大小(精确到 )(1)sinβ=0.4511;(2)cosβ=0.7857(3)tanβ=1.4036⌒课内练习:(1)AB=3,AC=1;(2)AC=4,BC=5.例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;故 BD=AC(1)例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,当堂训练一1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。sinA= , tanB=√3,则∠C=4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )A,相等 B,互余 C,互补 D,不确定。A75°BA例题赏析(1)计算: sin60°·tan60°+cos 2 45°=(2)如果tanA·tan30°=1,∠A=_________。(3)已知cosα<0.5,那么锐角α的取值范围( ) A、60°<α<90° B、 0°< α <60° C、30°< α <90° D、 0°< α <30°(4)如果√cosA – — + | √3 tanB –3|=012那么△ABC是( ) A、直角三角形 B、锐角三角形
C、钝角三角形 D、等边三角形。260° AD2当堂训练二
锐角,用计算器都可以求出它的函数值.反之,已知三角函数值能否求出相应的角度?例如,已知sinα=0.2974,求锐角α.按键顺序如下:17.30150783即α=17.30150783例1 根据下面的条件,求锐角β的大小(精确到 )(1)sinβ=0.4511;(2)cosβ=0.7857(3)tanβ=1.4036⌒课内练习:(1)AB=3,AC=1;(2)AC=4,BC=5.例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;故 BD=AC(1)例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,当堂训练一1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。sinA= , tanB=√3,则∠C=4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )A,相等 B,互余 C,互补 D,不确定。A75°BA例题赏析(1)计算: sin60°·tan60°+cos 2 45°=(2)如果tanA·tan30°=1,∠A=_________。(3)已知cosα<0.5,那么锐角α的取值范围( ) A、60°<α<90° B、 0°< α <60° C、30°< α <90° D、 0°< α <30°(4)如果√cosA – — + | √3 tanB –3|=012那么△ABC是( ) A、直角三角形 B、锐角三角形
C、钝角三角形 D、等边三角形。260° AD2当堂训练二
