1.1锐角三角函数(2)[下学期]
图片预览



文档简介
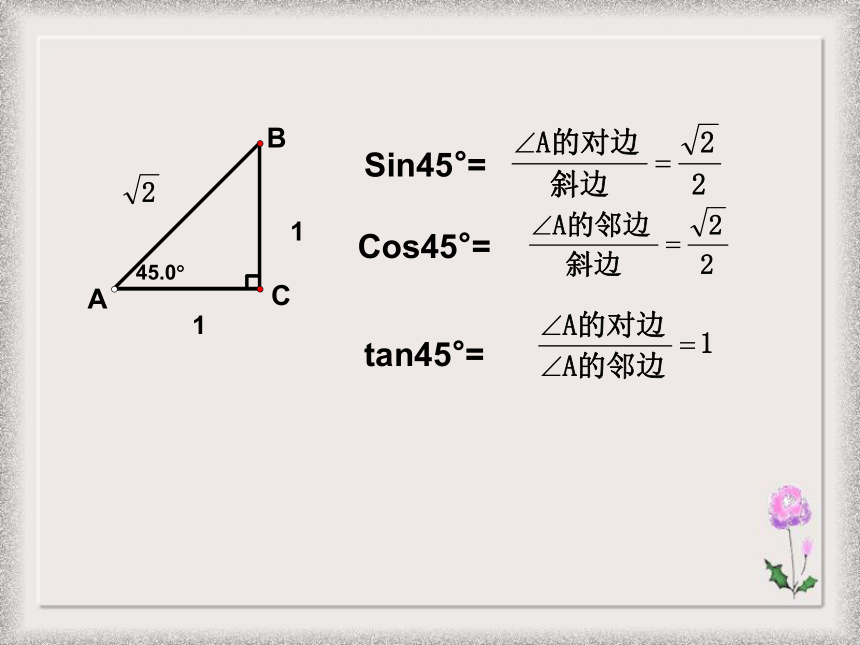
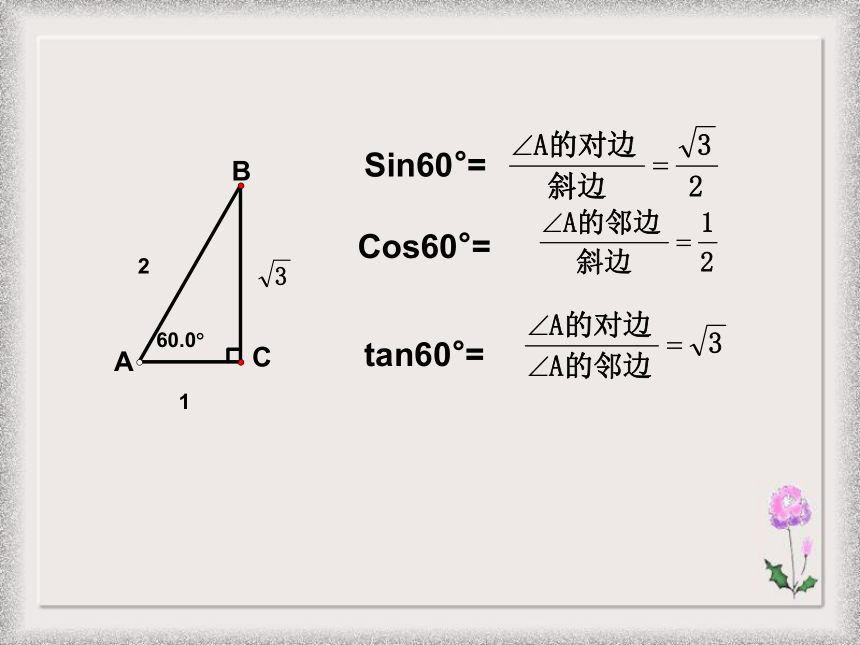
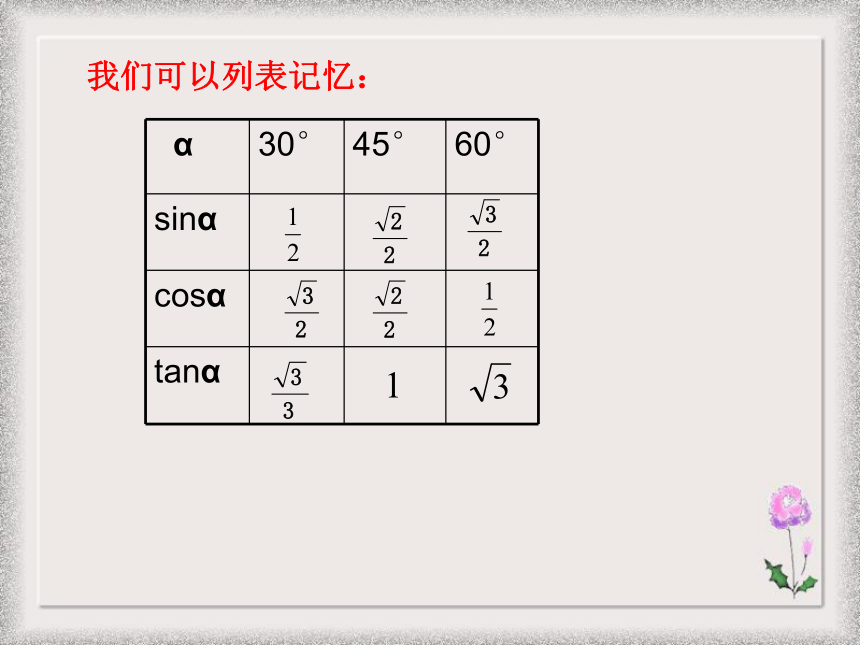
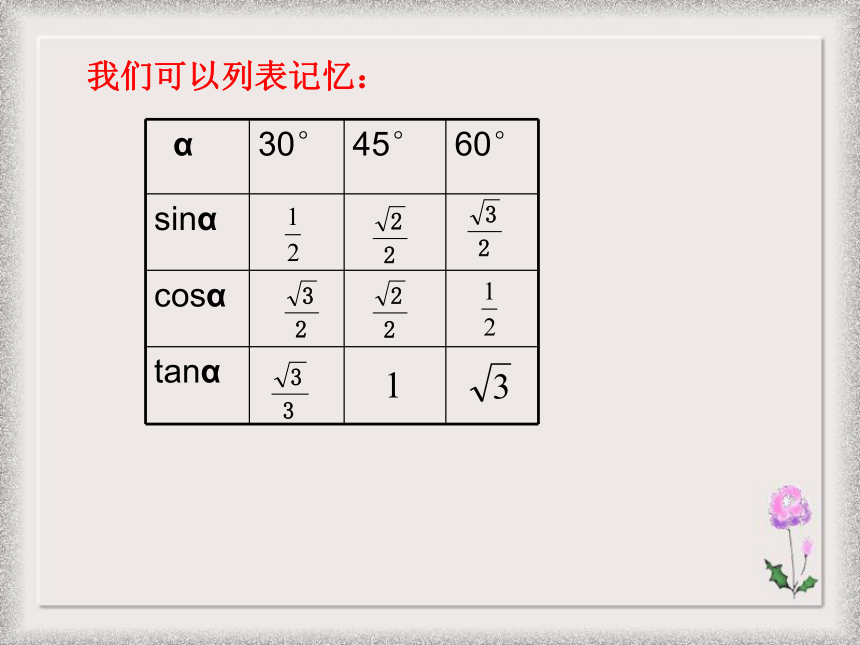
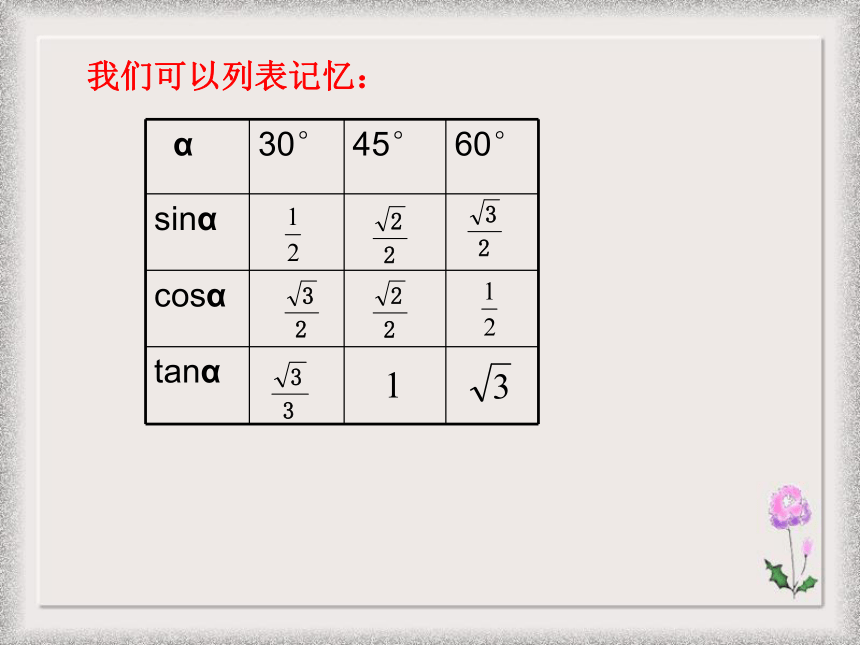
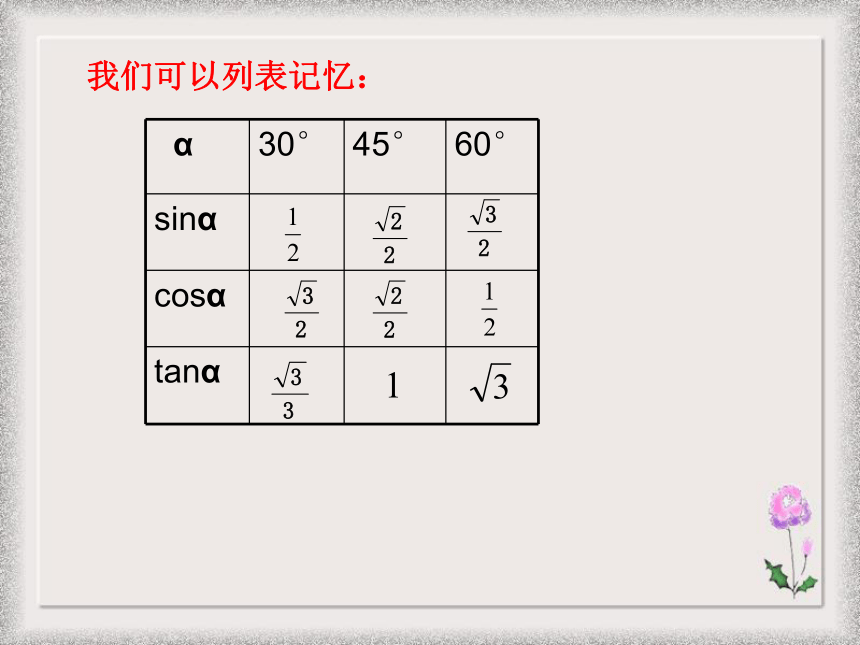
课件20张PPT。1.1锐角三角函数(2)浙教版九年级(下)新知探索:Sin30°=Cos30°=tan30°=Cos45°=tan45°=Sin45°=Sin60°=Cos60°=tan60°=我们可以列表记忆:我们可以列表记忆:我们可以列表记忆:我们可以列表记忆:例1.计算:利用特殊的三角函数值进行计算: (1)2sin30°- 3cos60 °(2)cos245°+tan60°·sin60°(3) cos30°- sin45°+tan45°· cos60° 老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.P8课内练习2,43.如图,在Rt△ABC中,∠C=90°,
∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.例2 如图(见课本),一位同学的手臂长65cm, 当他高举双臂时,指尖高出头顶35cm.问当他的手臂与水平方向成60°角时,指尖高出头顶多少cm(精确到0.1cm)?60°DCP9课内练习32.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少?练习 已知∠A为锐角,且cosA= ,
你能求出∠A的度数吗。例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).将实际问题数学化.解简单的三角方程例3.求适合下列各式的锐角α例4.已知 (α为锐角)
求三角函数的单调性 : 观察特殊角的三角函数表,发现规律: 课外思考:利用上述规律可以比较同名三角函数值的大小例4 填空:比较大小作业:1.书
2.同步5.求适合下列条件的锐角α
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.P8课内练习2,43.如图,在Rt△ABC中,∠C=90°,
∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.例2 如图(见课本),一位同学的手臂长65cm, 当他高举双臂时,指尖高出头顶35cm.问当他的手臂与水平方向成60°角时,指尖高出头顶多少cm(精确到0.1cm)?60°DCP9课内练习32.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少?练习 已知∠A为锐角,且cosA= ,
你能求出∠A的度数吗。例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).将实际问题数学化.解简单的三角方程例3.求适合下列各式的锐角α例4.已知 (α为锐角)
求三角函数的单调性 : 观察特殊角的三角函数表,发现规律: 课外思考:利用上述规律可以比较同名三角函数值的大小例4 填空:比较大小作业:1.书
2.同步5.求适合下列条件的锐角α
