3.1 直线和圆的位置关系[下学期]
图片预览



文档简介
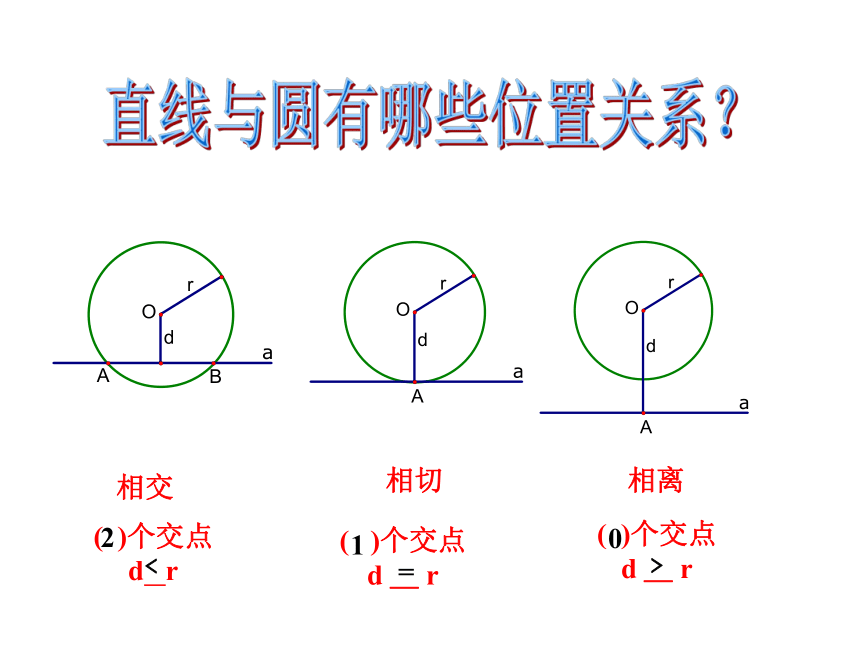
课件13张PPT。直线与圆的位置关系复习直线与圆有哪些位置关系?( )个交点
d _ r( )个交点
d _ r
( )个交点
d r 2﹤1=0﹥1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
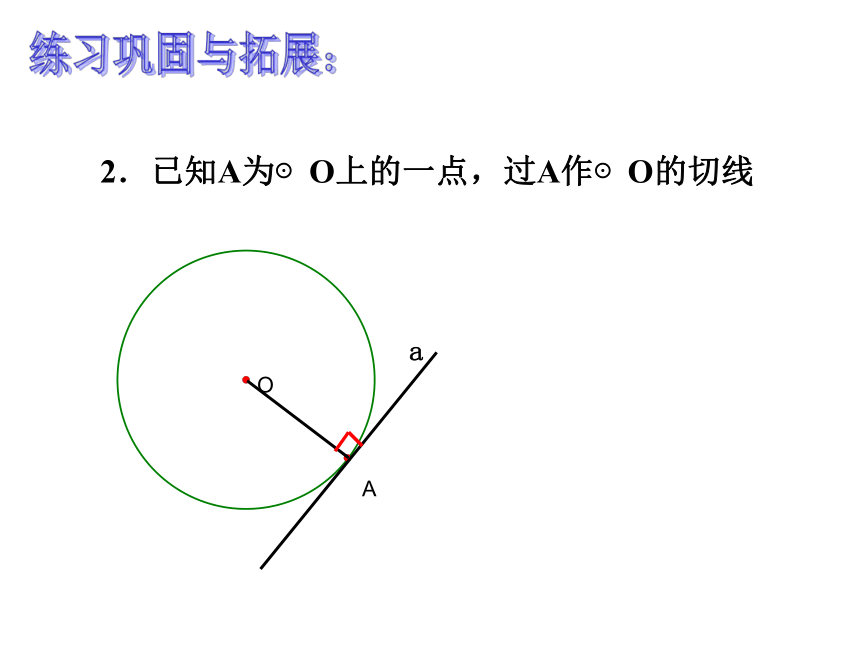
(3) r=4,d=7 ⊙O与a 相离相交相切基础练习:2.已知A为⊙O上的一点,过A作⊙O的切线练习巩固与拓展:2.切线性质:
(1)切线垂直于过切点的直径
1.切线的判定:
(1)定义 直线与圆只有一个交点
(2)d=r 圆心到直线的距离等于半径
(3)直线过半径的外端并且垂直于这条半径
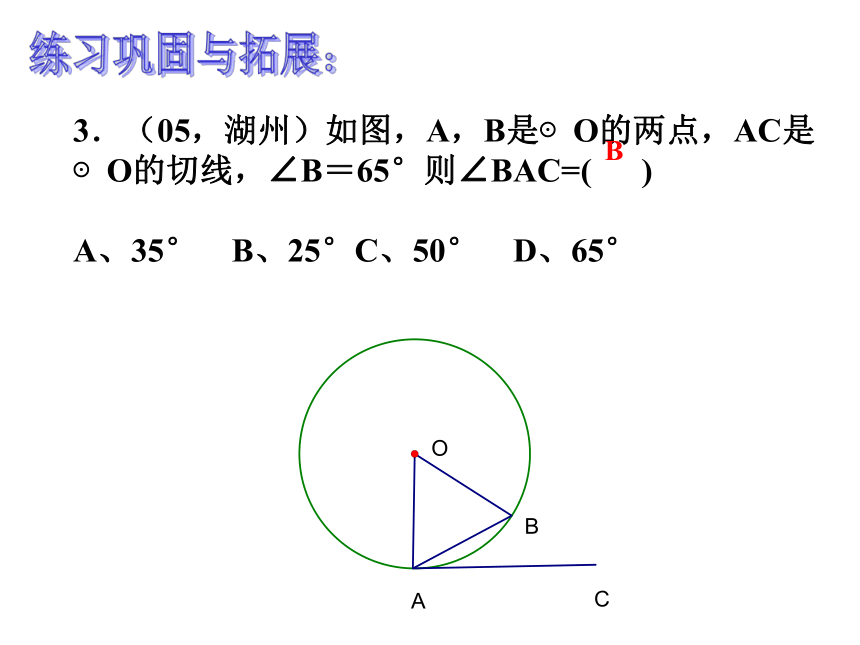
切线性质与判定 (2)d=r 圆心到直线的距离等于半径3.(05,湖州)如图,A,B是⊙O的两点,AC是⊙O的切线,∠B=65°则∠BAC=( ) A、35° B、25°C、50° D、65°B练习巩固与拓展:4、(05,温州)已知:PA为⊙O的切线,A为切点,OB交⊙O于点B ,PB=2,PA =4. ⊙O的半径r=练习巩固与拓展:24rr35、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙P的位置关系是…( )
A、相交 B、相切 C、相离 D、相切或相交D巩固与拓展6、(05,苏州)如图,AB是⊙O的直径,BC是⊙O的切线,AD∥CO,D是⊙O上的一点 (1)求证:△ADB∽△OBC ; (2)若AB=2,∠C=300 ,求AD的长。 (1)证明:
∵ AB是⊙O的直径,
BC是⊙O的切线
∴ ∠D= ∠ABC=90°
又∵ AD∥CO
∴ ∠A= ∠COB
∴ △ADB∽△OBC (2)
∵ △ADB∽△OBC,
∠ D =90°
∴ ∠C= ∠DBA=30°
∴AD= ?AB=1
巩固与拓展思考与探索: 7.如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E. 由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
8、如图,园林部门准备在公园的三条小道围成的地块内建造一个圆形喷水池,要求面积尽量大。请问如何建造圆的面积最大?当圆的面积最大时,圆的半径是多少?思考与探索:ABCOr小结:
1.直线与圆的三种位置关系:相交、相切、相离
2.直线与圆相切的判定与性质谢谢!
d _ r( )个交点
d _ r
( )个交点
d r 2﹤1=0﹥1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
(3) r=4,d=7 ⊙O与a 相离相交相切基础练习:2.已知A为⊙O上的一点,过A作⊙O的切线练习巩固与拓展:2.切线性质:
(1)切线垂直于过切点的直径
1.切线的判定:
(1)定义 直线与圆只有一个交点
(2)d=r 圆心到直线的距离等于半径
(3)直线过半径的外端并且垂直于这条半径
切线性质与判定 (2)d=r 圆心到直线的距离等于半径3.(05,湖州)如图,A,B是⊙O的两点,AC是⊙O的切线,∠B=65°则∠BAC=( ) A、35° B、25°C、50° D、65°B练习巩固与拓展:4、(05,温州)已知:PA为⊙O的切线,A为切点,OB交⊙O于点B ,PB=2,PA =4. ⊙O的半径r=练习巩固与拓展:24rr35、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙P的位置关系是…( )
A、相交 B、相切 C、相离 D、相切或相交D巩固与拓展6、(05,苏州)如图,AB是⊙O的直径,BC是⊙O的切线,AD∥CO,D是⊙O上的一点 (1)求证:△ADB∽△OBC ; (2)若AB=2,∠C=300 ,求AD的长。 (1)证明:
∵ AB是⊙O的直径,
BC是⊙O的切线
∴ ∠D= ∠ABC=90°
又∵ AD∥CO
∴ ∠A= ∠COB
∴ △ADB∽△OBC (2)
∵ △ADB∽△OBC,
∠ D =90°
∴ ∠C= ∠DBA=30°
∴AD= ?AB=1
巩固与拓展思考与探索: 7.如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E. 由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
8、如图,园林部门准备在公园的三条小道围成的地块内建造一个圆形喷水池,要求面积尽量大。请问如何建造圆的面积最大?当圆的面积最大时,圆的半径是多少?思考与探索:ABCOr小结:
1.直线与圆的三种位置关系:相交、相切、相离
2.直线与圆相切的判定与性质谢谢!
