3.2三角形的内切圆[下学期]
图片预览




文档简介
课件20张PPT。6.5 三角形的内切圆(一)引入新课
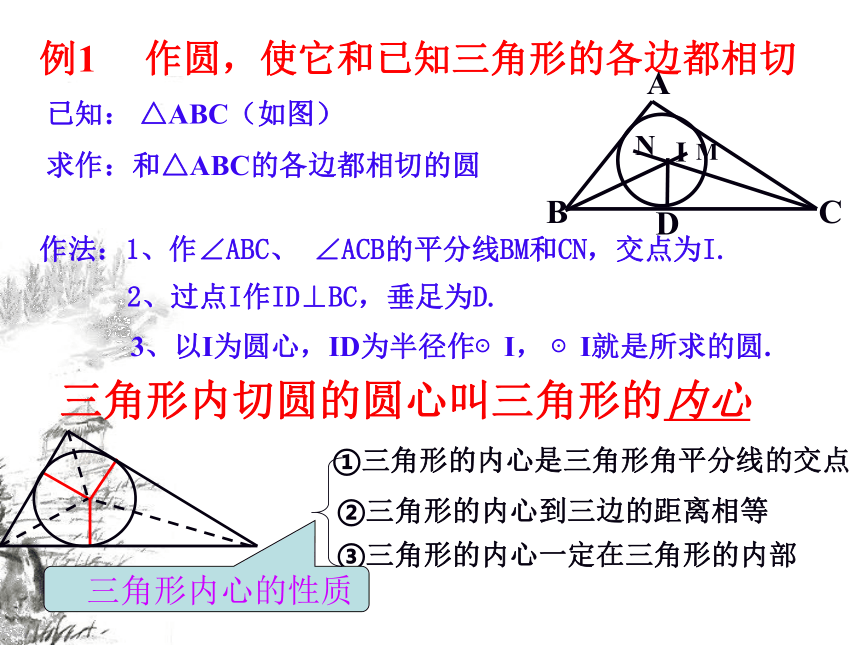
问题1:作圆的关键是什么?问题2:怎样确定圆心的位置?问题3:圆心的位置确定后怎样确定圆的半径?(确定圆心和半径)(作两条角平分线,其交点就是圆心的位置)(过圆心作三角形一边的垂线,垂线段的长就是圆的半径)例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆问题4:在这块三角形材料上还能裁下更大的圆吗?(不 能) 任何一个三角形都只有一个内切圆(二)例题分析3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆ABC作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
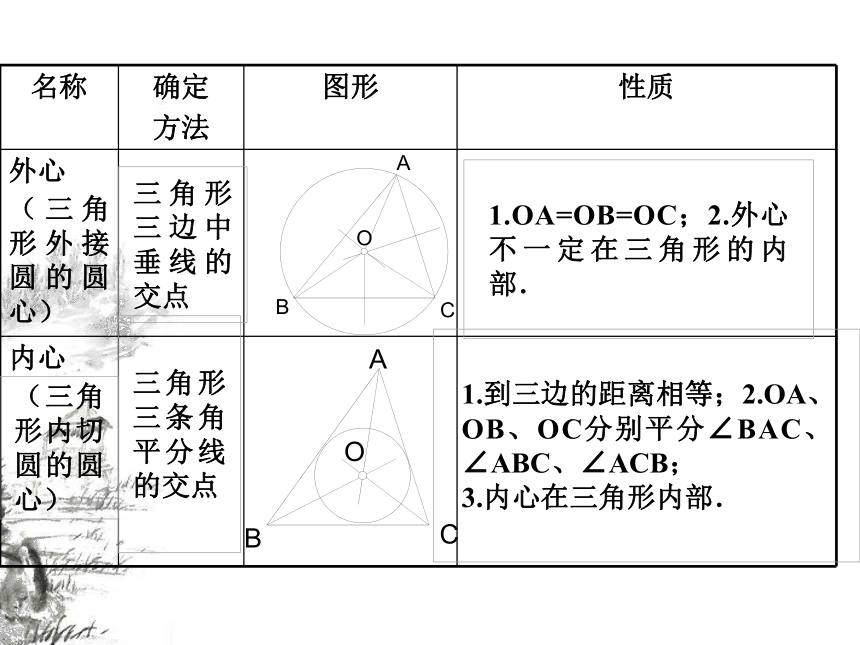
三角形内切圆的圆心叫三角形的内心②三角形的内心到三边的距离相等①三角形的内心是三角形角平分线的交点③三角形的内心一定在三角形的内部(三角形外接圆的圆心)(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
20130试探讨∠BOC与∠A之间存在怎样的数量关系?
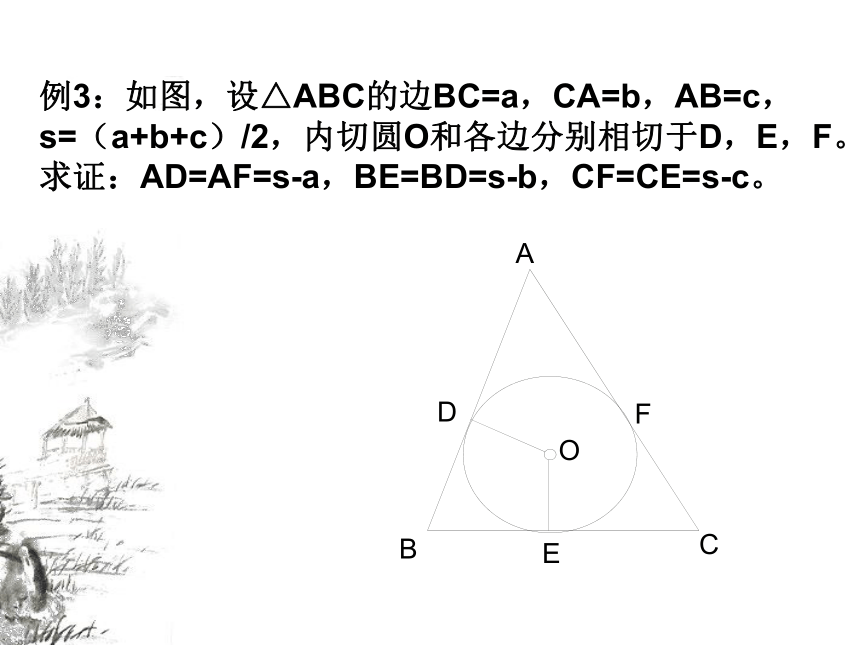
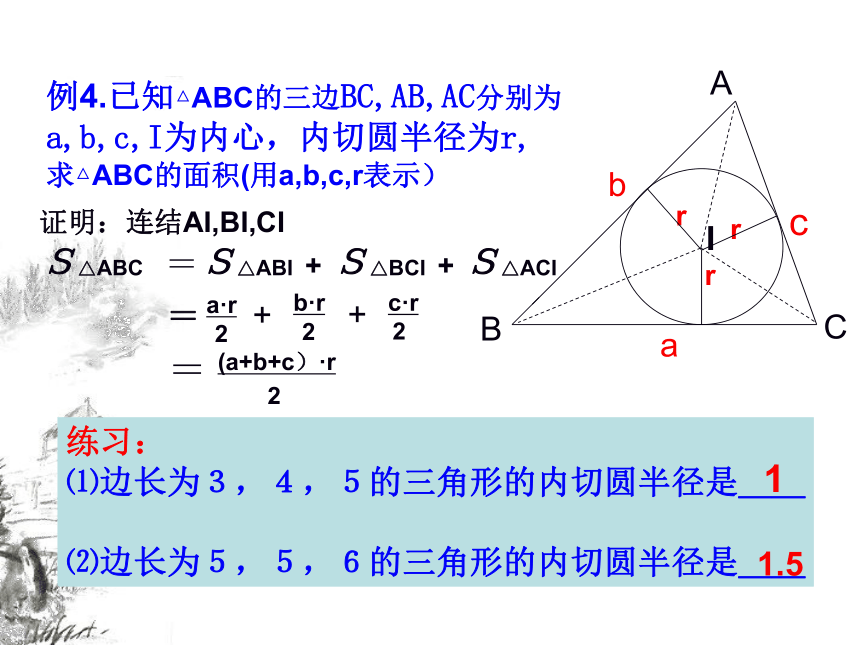
请说明理由.例3:如图,设△ABC的边BC=a,CA=b,AB=c, s=(a+b+c)/2,内切圆O和各边分别相切于D,E,F。 求证:AD=AF=s-a,BE=BD=s-b,CF=CE=s-c。例4.已知△ABC的三边BC,AB,AC分别为
a,b,c,I为内心,内切圆半径为r,
求△ABC的面积(用a,b,c,r表示)证明:连结AI,BI,CI
S△ABC =S△ABI + S△BCI + S△ACI练习:
⑴边长为3,4,5的三角形的内切圆半径是__
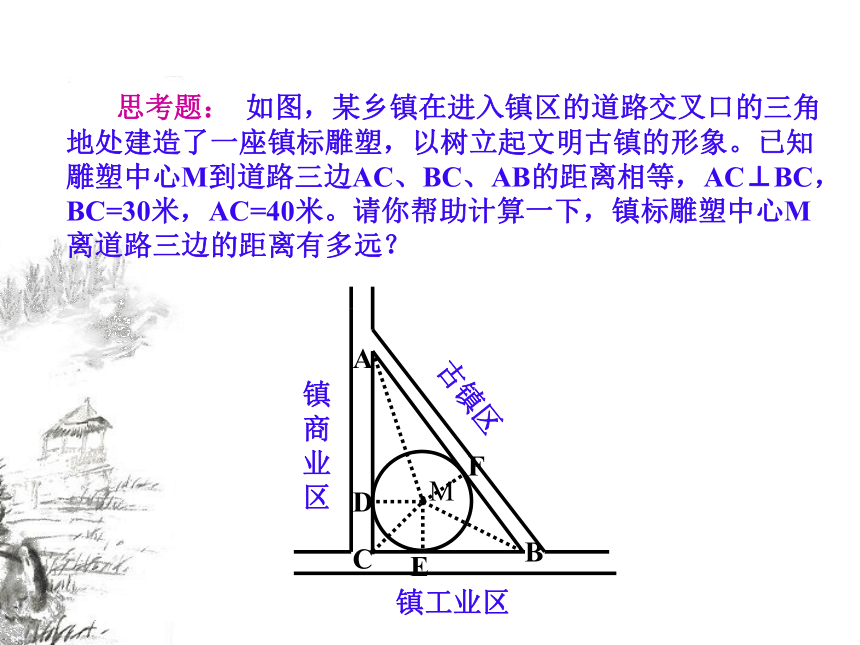
⑵边长为5,5,6的三角形的内切圆半径是__11.5 思考题: 如图,某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米。请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?
解: ∵雕塑中心M到道路三边的距离相等
∴点M是△ABC的内心,连结AM、BM、CM,设⊙M的半径为r米,⊙M分别切AC、BC、AB于点D、E、F,则MD⊥AC, ME ⊥BC, MF ⊥AB,则MD= ME= MF=r,
∵在Rt △ABC 中,AC=40,BC=30, ∴AB=50
∵ △ABC的面积为 AC·BC= × 40×30= 600,又∵ △ABC
的面积为 (AC·MD+BC ·ME+AB ·MF)=20 r+15 r+25 r=60 r
∴60 r= 600, r=10
答:镇标雕塑中心离道路三边的距离为10米。
(三)、特殊三角形外接圆、内切圆半径的求法:ABCOIabc直角三角形外接圆、内切圆半径的求法ABCOD等边三角形的内切圆半径r与外接圆半径R的求法:基本思路:构造Rt△BOD,BO为外接圆半径R,DO为内切圆半径r。Rr1. 定义:和多边形各边都相切的圆
叫做 ,这个
多边形叫做 。
多边形的内切 圆圆的外切多边形内切外切2.如上图,四边形DEFG是⊙O的 四边形,
⊙O是四边形DEFG的 圆.思考:我们所学的平行四边形,矩形,菱形,正方
形,等腰梯形中,哪些四边形一定有内切圆?(菱形,正方形一定有内切圆)(四)多边形的内切圆3.如上图,四边形DEFG是圆O的外切四边形,则它有什么性质?(五)小结 1.学习了三角形内切圆、三角形的内心、圆的外切三角形、多边形的内切圆、圆的外切多边形的概念.
2.利用作三角形的内角平分线,任意两条角平分线的交点就是内切圆的圆心,交点到任意一边的距离是圆的半径.
3.在学习有关概念时,应注意区别“内”与“外”,“接”与“切”;还应注意“连结内心和三角形顶点”这一辅助线的添加和应用.
4.学习了如何计算三角形的内切圆半径,尤其是直角三角形的内切圆半径. 1 .判断题:
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
错错对对 错 对(六)能力训练3、菱形ABCD中,周长为40,∠ABC=120°,则内切圆的半径为( )(A) (B) (C) (D) 4、如图,⊙O是△ABC的内切圆,D、E、F是切点,∠A=50°,∠C=60°,则∠DOE=( )(A)70°(B)110°C)120°(D)130° 2、下列图形中,一定有内切圆的四边形是( )(A)梯形 (B)菱形 (C)矩形 (D)平行四边形BDB5、正三角形的内切圆半径、外接圆半径和高的比为( )(A)1∶ ∶ (B)1∶2∶
(C)1∶ ∶2 (D)1∶2∶3 6、存在内切圆和外接圆的四边形一定是( )(A)矩形 (B)菱形 (C)正方形 (D)平行四边形DC(1)求证:ID=BD;
(2)设△ABC外接圆半径R=3,ID=2,AD=x,DE=y,当点A在优弧BC上运动时,求函数y与自变量x间的函数关系式,并指出自变量的取值范围.提示:(1)略;
(2)由 ,∴ ,
∵BD∴自变量x的取值范围是2为r,求证:AI:r=2R:ID
问题1:作圆的关键是什么?问题2:怎样确定圆心的位置?问题3:圆心的位置确定后怎样确定圆的半径?(确定圆心和半径)(作两条角平分线,其交点就是圆心的位置)(过圆心作三角形一边的垂线,垂线段的长就是圆的半径)例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆问题4:在这块三角形材料上还能裁下更大的圆吗?(不 能) 任何一个三角形都只有一个内切圆(二)例题分析3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆ABC作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
三角形内切圆的圆心叫三角形的内心②三角形的内心到三边的距离相等①三角形的内心是三角形角平分线的交点③三角形的内心一定在三角形的内部(三角形外接圆的圆心)(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
20130试探讨∠BOC与∠A之间存在怎样的数量关系?
请说明理由.例3:如图,设△ABC的边BC=a,CA=b,AB=c, s=(a+b+c)/2,内切圆O和各边分别相切于D,E,F。 求证:AD=AF=s-a,BE=BD=s-b,CF=CE=s-c。例4.已知△ABC的三边BC,AB,AC分别为
a,b,c,I为内心,内切圆半径为r,
求△ABC的面积(用a,b,c,r表示)证明:连结AI,BI,CI
S△ABC =S△ABI + S△BCI + S△ACI练习:
⑴边长为3,4,5的三角形的内切圆半径是__
⑵边长为5,5,6的三角形的内切圆半径是__11.5 思考题: 如图,某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米。请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?
解: ∵雕塑中心M到道路三边的距离相等
∴点M是△ABC的内心,连结AM、BM、CM,设⊙M的半径为r米,⊙M分别切AC、BC、AB于点D、E、F,则MD⊥AC, ME ⊥BC, MF ⊥AB,则MD= ME= MF=r,
∵在Rt △ABC 中,AC=40,BC=30, ∴AB=50
∵ △ABC的面积为 AC·BC= × 40×30= 600,又∵ △ABC
的面积为 (AC·MD+BC ·ME+AB ·MF)=20 r+15 r+25 r=60 r
∴60 r= 600, r=10
答:镇标雕塑中心离道路三边的距离为10米。
(三)、特殊三角形外接圆、内切圆半径的求法:ABCOIabc直角三角形外接圆、内切圆半径的求法ABCOD等边三角形的内切圆半径r与外接圆半径R的求法:基本思路:构造Rt△BOD,BO为外接圆半径R,DO为内切圆半径r。Rr1. 定义:和多边形各边都相切的圆
叫做 ,这个
多边形叫做 。
多边形的内切 圆圆的外切多边形内切外切2.如上图,四边形DEFG是⊙O的 四边形,
⊙O是四边形DEFG的 圆.思考:我们所学的平行四边形,矩形,菱形,正方
形,等腰梯形中,哪些四边形一定有内切圆?(菱形,正方形一定有内切圆)(四)多边形的内切圆3.如上图,四边形DEFG是圆O的外切四边形,则它有什么性质?(五)小结 1.学习了三角形内切圆、三角形的内心、圆的外切三角形、多边形的内切圆、圆的外切多边形的概念.
2.利用作三角形的内角平分线,任意两条角平分线的交点就是内切圆的圆心,交点到任意一边的距离是圆的半径.
3.在学习有关概念时,应注意区别“内”与“外”,“接”与“切”;还应注意“连结内心和三角形顶点”这一辅助线的添加和应用.
4.学习了如何计算三角形的内切圆半径,尤其是直角三角形的内切圆半径. 1 .判断题:
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
错错对对 错 对(六)能力训练3、菱形ABCD中,周长为40,∠ABC=120°,则内切圆的半径为( )(A) (B) (C) (D) 4、如图,⊙O是△ABC的内切圆,D、E、F是切点,∠A=50°,∠C=60°,则∠DOE=( )(A)70°(B)110°C)120°(D)130° 2、下列图形中,一定有内切圆的四边形是( )(A)梯形 (B)菱形 (C)矩形 (D)平行四边形BDB5、正三角形的内切圆半径、外接圆半径和高的比为( )(A)1∶ ∶ (B)1∶2∶
(C)1∶ ∶2 (D)1∶2∶3 6、存在内切圆和外接圆的四边形一定是( )(A)矩形 (B)菱形 (C)正方形 (D)平行四边形DC(1)求证:ID=BD;
(2)设△ABC外接圆半径R=3,ID=2,AD=x,DE=y,当点A在优弧BC上运动时,求函数y与自变量x间的函数关系式,并指出自变量的取值范围.提示:(1)略;
(2)由 ,∴ ,
∵BD
