浙教版九年级下 第四章投影与三视图 全章教案[下学期]
文档属性
| 名称 | 浙教版九年级下 第四章投影与三视图 全章教案[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-23 19:39:00 | ||
图片预览



文档简介
第19周第3课时上课时间1月4日(星期四)累计教案83个
课题:4.1投影与盲区
教学目标:
1、经历实践、探索的过程,了解视点、视线、视角与盲区的概念;
2、体会视点、视线、视角、盲区在现实生活中的应用;
3、了解视点、视线、视角、盲区与中心投影的关系,感受其在生活中的实用价值。
教学重点:应用盲区的意义解释简单的现实现象。
教学难点:在简单的平面图和立体图中表示视线、视角和盲区。
教学过程:
一、创设情境,引入新课
(出示投影)你知道为什么飞机超低空飞行时,雷达很难发现它?
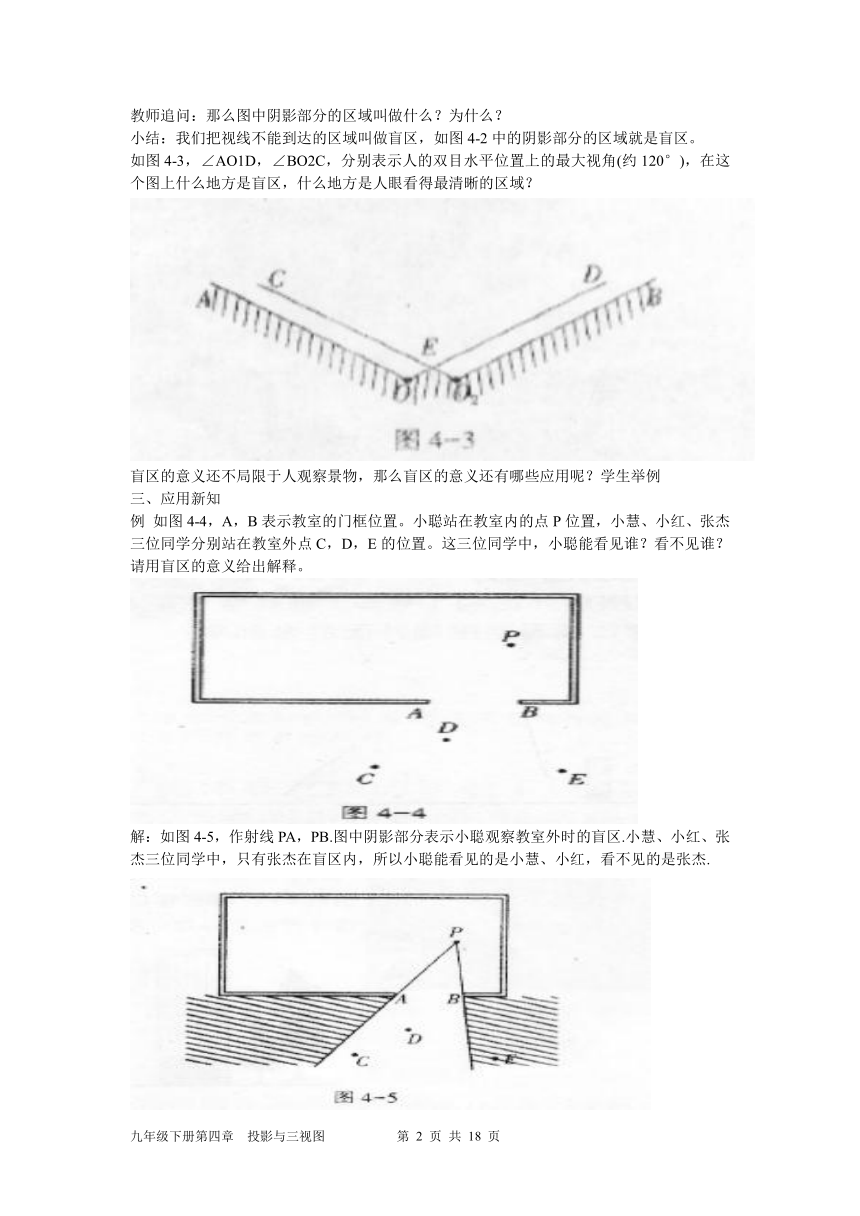
下图是人观察事物时的直观图,在这个图上涉及了哪些数学知识?(视线,视角,视点)
你能试着给它们下定义吗?
人在观察目标时,从眼睛到目标的射线叫做视线,眼睛所在的位置叫做视点,有公共视点的两条视线所成的角叫做视角。
做一做:课本:第70页
强调:视角与仰角和俯角的区别。
二、盲区的概念
如图4-2,小明在点O能看见站在幕布后面点C的小华吗?如果小明的位置不变,小华应怎样移动自己的位置,才能使小明看到自己?为什么?
学生讨论后得出:不能;移到幕布前∠AOB的范围内;因为小华在幕布后面的区域是小明视线不能到达的区域,要使小明看到自己,必须要移到小明视线能到达的区域。
教师追问:那么图中阴影部分的区域叫做什么?为什么?
小结:我们把视线不能到达的区域叫做盲区,如图4-2中的阴影部分的区域就是盲区。
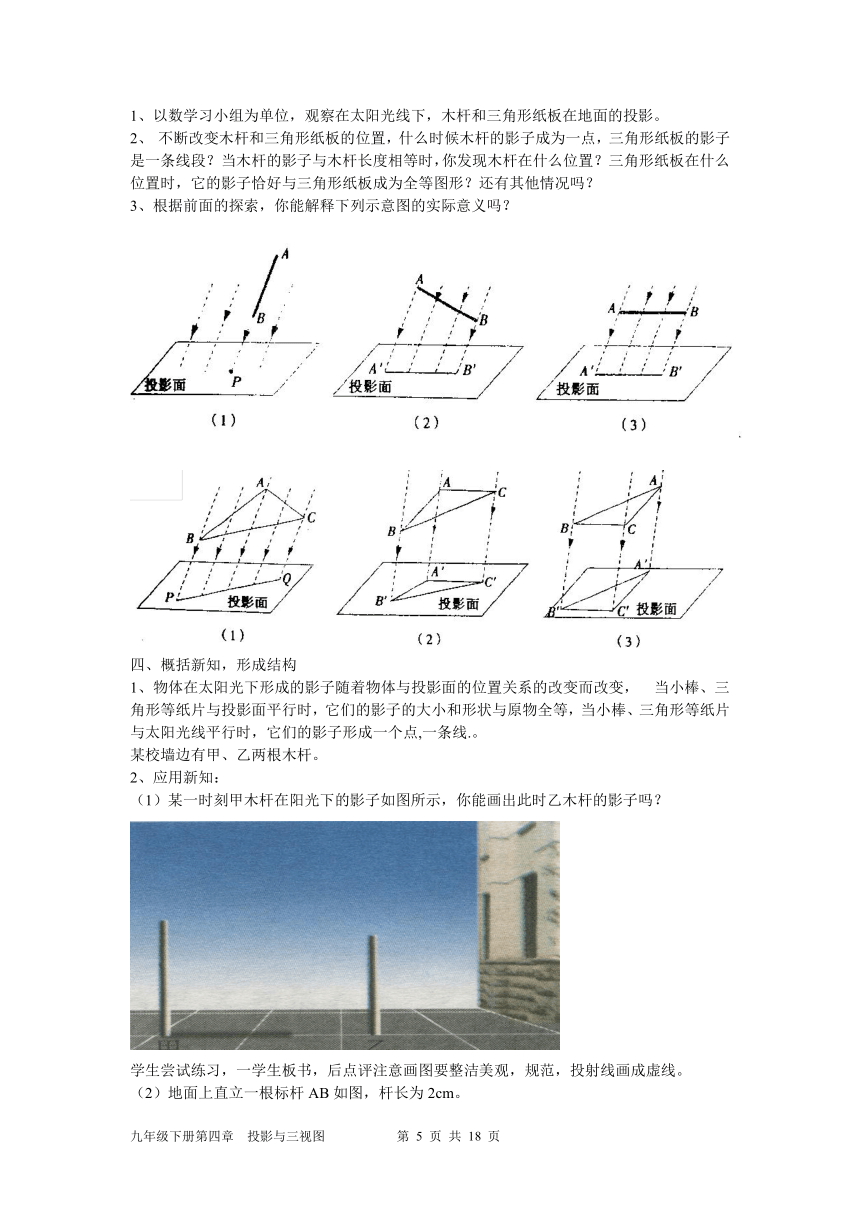
如图4-3,∠AO1D,∠BO2C,分别表示人的双目水平位置上的最大视角(约120°),在这个图上什么地方是盲区,什么地方是人眼看得最清晰的区域?
盲区的意义还不局限于人观察景物,那么盲区的意义还有哪些应用呢?学生举例
三、应用新知
例 如图4-4,A,B表示教室的门框位置。小聪站在教室内的点P位置,小慧、小红、张杰三位同学分别站在教室外点C,D,E的位置。这三位同学中,小聪能看见谁?看不见谁?请用盲区的意义给出解释。
解:如图4-5,作射线PA,PB.图中阴影部分表示小聪观察教室外时的盲区.小慧、小红、张杰三位同学中,只有张杰在盲区内,所以小聪能看见的是小慧、小红,看不见的是张杰.
练习:课本第71页课内练习和作业题(由学生独立完成,后指名学生口答或板书)
四、 小结:
通过这节课的学习你学会了什么?你有什收获与困惑?
五、布置作业:见课课通第186页----第187页。
第19周第4课时上课时间1月5日(星期五)累计教案84个
课题:4.2投影(1)
教学目标:
1、经历实践探索,了解投影、投影面、及平行投影的概念;
2、体会并理解平行投影的特征,利用光的影子解决生活中的实际问题。
教学重点:理解平行投影的特征;
教学难点:在投影面上画出平面图形的平行投影。
教学过程:
一、创设情境
你看过皮影戏吗 皮影戏又名“灯影子”,是我国民间一种古老而奇特的戏曲艺术,在关中地区很为流行。皮影戏演出简便,表演领域广阔,演技细腻,活跃于广大农村,深受农民的欢迎。
放映电影《小兵张嘎》部分片段 ---小胖墩和他爸在日军炮台内为日本鬼子表演皮影戏
二、你知道吗
出示投影:
北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.
问题:那什么是投影呢?
物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影现象。光线叫做投射线,影子(也叫投影)所在的平面叫做投影面.
出示投影让学生感受在日常生活中的一些投影现象。
因为太阳离我们非常遥远,所以太阳光线可以看成平行光线,像这样的光线所形成的投影成为平行投影 ( parallel projection ).
三、问题探究(在课前布置,以数学学习小组为单位)
合作学习:在平行投影下,线段和平面图形的投影与图形本身、投影面、投射线之间的相对位置有什么关系? 请就此问题作一探讨。
1、以数学习小组为单位,观察在太阳光线下,木杆和三角形纸板在地面的投影。
2、 不断改变木杆和三角形纸板的位置,什么时候木杆的影子成为一点,三角形纸板的影子是一条线段?当木杆的影子与木杆长度相等时,你发现木杆在什么位置?三角形纸板在什么位置时,它的影子恰好与三角形纸板成为全等图形?还有其他情况吗?
3、根据前面的探索,你能解释下列示意图的实际意义吗?
四、概括新知,形成结构
1、物体在太阳光下形成的影子随着物体与投影面的位置关系的改变而改变, 当小棒、三角形等纸片与投影面平行时,它们的影子的大小和形状与原物全等,当小棒、三角形等纸片与太阳光线平行时,它们的影子形成一个点,一条线.。
某校墙边有甲、乙两根木杆。
2、应用新知:
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出此时乙木杆的影子吗?
学生尝试练习,一学生板书,后点评注意画图要整洁美观,规范,投射线画成虚线。
(2)地面上直立一根标杆AB如图,杆长为2cm。
①当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
②当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?并画出投影示意图;
(3)一个正方形纸板ABCD和投影面平行(如图),投射线和投影面垂直,点C在投影面的对应点为C’,请画出正方形纸板的投影示意图。
五、学习反思:
我们这节课学习了什么知识?
(1) 物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影;
(2) 太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影
(3) 物体在太阳光下形成的影子随着物体与投影面的位置关系的改变而改变,
1.当小棒、三角形等纸片与投影面平行时,它们的影子的大小和形状与原物全等.
2当小棒、三角形等纸片与太阳光线平行时,它们的影子形成一个点,一条线.
六、作业:
1、见课课通第188页,注意:第15题要解释题意
2、设计题:
北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.请通过查阅资料,上互联网等途径,收集我国古代有关日晷的历史背景,探索用日晷测定时刻的数学原理,并就此写一篇简要的报告.
第20周第1课时上课时间1月8日(星期一)累计教案85个
课题:4.2投影(2)
教学目标:
1、理解中心投影的概念,掌握和区别中心投影的投射线和平行投影的投射线具有不同的性质;
2、在观察、比较与归纳的探索过程zhogn,发现空间想象能力。
教学重点:中心投影的概念和区分中心投影和平行投影的区别;
教学难点:在投影面上画出平面图形的中心投影。
教学过程:
一、创设情景
投影出示:手影戏
二、归纳、应用新知
1、像皮影戏与手影戏这样由同一点的投射线所形成的投影叫做中心投影。
2、由于中心投影与平行投影的投射线具有不同的性质,因此,在这两种投影下,物体的影子也就有明显的差别。如图4-14,当线段AB与投影面平行时,AB的中心投影A‘B’把线段AB放大了,且AB∥A’B‘,△OAB~ OA‘B’.又如图4-15,当△ABC所在的平面与投影面平行时, △ABC的中心投影△A‘B’C‘也把△ABC放大了,从△ABC到△A‘B’C‘是我们熟悉的位似变换。
3、请观察平行投影和中心投影,它们有什么相同点与不同点?
平行投影与中心投影的区别与联系
区别 联系
光线 物体与投影面平行时的投影
平行投影 平行的投射线 全等 都是物体在光线的照射下,在某个平面内形成的影子。(即都是投影)
中心投影 从一点出发的投射线 放大(位似变换)
4、应用新知:(1)例2 图4-16的两幅图表示两根标杆在同一时刻的投影.请在图中画出形成投影的光线.它们是平行投影还是中心投影?并说明理由。
解:分别连结标杆的顶端与投影上的对应点(图4-17).很明显,图(1)的投射线互相平行,是平行投影.图(2)的投射线相交于一点,是中心投影。
(2)练习:课本第78页第1、2题
(3)例3 : 图4-18是两棵小树在路灯下的影子.请画出形成树影的光线,确定光源的位置.
解: 如图4-19,连结CB,FE,并延长相交于点O,则OC,OF就是形成树影的光线,点O就是光源所在的位置。
(4)练习:课本作业题第2、3、4 题。其中第4题要利用三角形相似知识有一定难度,要适当点拨。
三、小结:
1、由同一点出发的投射线所形成的投影叫做中心投影;
2、区别中心投影和平行投影关键在于投影线是否相交,若投射线相交于一点,则是中心投影,否则就是平行投影。
四、作业
见课课通第190—191页。
第20周第2课时上课时间1月9日(星期二)累计教案86个
课题:4.3简单物体的三视图(1)
教学目标:
1、了解正投影和简单立体图形的三视图的概念;
2、经历探索简单立体图形的三视图的画法,能识别物体的三视图;
3、培养动手实践能力,发展空间想象能力。
教学重点:简单立体图形的三视图的概念和画法
教学难点:简单立体图形的三视图的画法
教学过程:
一、创设情境,引入新课
“蒙古包”是蒙古族牧民住房的称呼。“包”,满语是“家”、“屋”的意思。蒙古族作为我国古老的游牧民族之一,他们的生活习性带有浓厚的游牧色彩。自古以来,这个生活在广阔的草原上,逐水草而居,以放牧牛羊为生的民族,大部分都从事着草原畜牧业。由于需要频繁地搬家,住房就必须是能够随意移动的活动房,古代又称这种活动房为“穹庐”、“毡帐”等,俗称“毡房”、“帐房”等。
如图所示的蒙古包的上部是圆锥,下部是圆柱体,你能画出它的三视图吗?
三视图与投影有什么关系?
指出:在平行投影中,如果投射线垂直于投影面,那么这种投影就称为正投影。
二、合作学习,探究新知
1、合作学习
这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
物体的正投影从一个方向反映了物体的形状和大小,为了全面地反映一个物体的形状和大小,我们常常再选择正面和侧面两个投影面,画出物体的正投影。
2、如图4-21,直三棱柱的正面方向的正投影是一个和矩形A1ACC1全等的矩形,这个矩形上、下两条边中点的连线,表示侧棱BB1的正投影;从左到右在侧投影面上的正投影也是一个矩形,它的一组对边等于直三棱柱的高,另一组对边等于直三棱柱底面三角形AC边上的高。
(1)你能试着画出它的三视图吗?
(2)如图4-21,这个直三棱柱的正面方向的正投影是什么形状?大小如何?你能描述一下吗?
(3)从左到右在侧投影面上的正投影是什么形状?大小如何?你能描述一下吗?
(4)分别转动水平和侧面的两个投影面,使三个正投影处于同一平面(如图4-22),就是我们所熟悉的三视图.
通过以上的学习,你有什么发现?
物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图,水平投影面上的正投影就是俯视图,侧投影面上的正投影就是左视图
三、应用新知
1、完成课本做一做
2、例1 一个圆锥如图4-23,底面直径为8㎝,高6㎝,画出它的三视图(比例为1:4)
分析:这个圆锥在正面的正投影是一个底边长为8㎝,高6㎝的等腰三角形;在水平面上的正投影是直径为8㎝的圆;在侧面上的正投影与正面上的正投影相同.
3、练习:课本第82页口答课内练习第1、2,作业题第2、3题和第4、5题(指名两学生板演)
四、小结
1、画一个立体图形的三视图时要考虑从某一个方向看物体获得的平面图形的形状和大小,不要受到该方向的物体结构的干扰。
2、在画三视图时,三个三视图不要随意乱放,应做到俯视图在主视图的下方,左视图在主视图的右边,三个视图之间保持:长对正,高平齐,宽相等。
五、作业:见课课通
第20周第3课时上课时间1月10日(星期三)累计教案87个
课题:简单物体的视图(2)
教学目标:
1、学会根据物体的三视图描述出几何体的基本形状或实物原型;
2、经历探索简单的组合几何体的三视图的画法,进一步发展空间想象能力。
教学重点与难点:根据物体的三视图描述出几何体的基本形状或实物原型
教学过程:
一、复习引入
说一说:直三棱柱、圆柱、圆锥、球的三视图
做一做:画出下列几何体的三视图
讲一讲:你知道正投影与三视图的关系
二、新课学习
例1 一个蒙古包如图所示,它上部的圆锥部分和下部的圆柱部分的高都是2m,底面直径为3m,请以1:200的比例画出它的三视图.
例2 一个六角螺帽的毛坯如图,底面正六边形的边长为250mm,高为 200mm,内孔直径为200mm.请画出六角螺帽毛坯的三视图.
3、课本的练习和作业题
三、小结:
1、一个视图不能确定物体的空间形状,根据三视图要描述几何体或实物原型时,必须将各视图对照起来看。
2、一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。例如:正方体的主视图是正方形,但主视图是正方形的几何体有直三棱柱、长方体、圆柱等。
3、对于较复杂的物体,有三视图形象出物体的原型,应搞清三个视图之间的前后、左右、上下的对应关系。
四、作业
见课课通地195---197页
第20周第4课时上课时间1月11日(星期四)累计教案88个
课题:第四章投影与三视图 复习
教学目标:
1、通过复习系统掌握本章知识,
2、体验数学来源于实践,又作用于实践。
3、提高解决问题分析问题的能力。
4、培养空间想象能力。
教学重点:投影和三视图
教学难点:画三视图
教学过程:
一、以提问形式小结本章知识
1、本章知识结构框架:
2、填空:
(1)人在观察目标时,从眼睛到目标的 叫做视线。 所在的位置叫做视点,有公共 的两条 所成的角叫做视角。
视线不能到达的区域叫做 。
(2)物体在光线的照射下,在某个 内形成的影子叫做 ,这时光线叫做 ,投影所在的 叫做投影面。
由 的投射线所形成的投影叫做平行投影。
由 的投射线所形成的投影叫做中心投影。
(3)在平行投影中,如果投射线 垂直于投影面,那么这种投影就称为正投影。
(4)物体的三视图是物体在三个不同方向的 。
上的正投影就是主视图,水平面上的正投影就是 , 上的正投影就是左视图。
二、例题讲解
例1、(1)在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A、小明的影子比小强的影子长 B、小明的影子比小强的影子短
C、小明和小强的影子一样长 D、无法判断谁的影子长
分析:阳光是平行光线,出现平行投影。路灯是点光源,是中心投影,形成的影子是不一样的
例2、如图所示图形是一个多面体的三视图,请根据视图说出该多面体的具体名称。
分析:从俯视图上看,该立体图形是个对称图形,从主视图、左视图上看,正面和左面都是等腰三角形,因此我们可以想象,该立体图形是正四棱锥。
例3、A、B 表示教室门口,张丽在教室内,王明、钱勇、李杰三同学在教室外,位置如图所示,张丽能看得见三位同学吗?请说明理由。
分析:画出最大视野也就是最大视角,就能确定盲区。
例4、如图,小王、小李及一根电线杆在灯光下的影子。
(1)确定光源的位置;
(2)在图中画出表示电线杆高度的线段。
分析:由条件易知,本题属于中心投影问题,根据中心投影的特点,物体与影子对应点的连线必须经过光源,因此我们可以利用两线的交点来求光源的位置。
例5、如图,是由一些大小相同的小正方体组成的简单的几何体的主视图和俯视图。
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值。
分析:左视图为侧视图,由于几何体只知道主视图和俯视图,那么左视图就不是唯一的,而主视图表示几何体共有三层,所以侧视图有多种可能,俯视图只看见5个小正方体,这5个正方体可分布在1、2、3层。
三、课外作业:见课本第86页的目标与评定。
第20周第5、6课时上课时间1月12日(星期五)累计教案89、90个
课题:第四章投影与三视图 测试卷
姓名: 分数:
一、精心选一选(每小题5分,共50分)
1.圆形的物体在太阳光的投影下是 ( )
(A)圆形. (B)椭圆形. (C)线段. (D)以上都不可能.
2.如图所示的圆台的上下底面与投影线平行,圆台的正投影是 ( )
(A)矩形. (B)两条线段.
(C)等腰梯形. (D)圆环.
3.如图摆放的几何体的左视图是 ( )
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
(A)小明的影子比小强的影子长. (B)小明的影子比小强的影子短.
(C)小明的影子和小强的影子一样长. (D)无法判断谁的影子长.
5.“圆柱与球的组合体”如图所示,则它的三视图是 ( )
6.下列左边的主视图和俯视图对应右边的哪个物体 ( )
7.小明在操场上练习双杠时,在练习的过程中他发现在地上双杠的两横杠的影子 ( )
(A)相交. (B)平行. (C)垂直. (D)无法确定.
8.在一个晴朗的好天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是 ( )
(A)上午. (B)中午. (C)下午. (D)无法确定.
9.如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是 ( )
(A)①②③④. (B)④①③②. (C)④②③①. (D)④③②①.
10.如图是“马头牌”冰激凌模型图,它的三视图是 ( )
二、耐心填一填(每小题4分,共20分)
11.右图是基本几何体的三视图,该基本几何体为 .
12.皮影戏中的皮影是由投影得到的 .
13.为测量旗杆的高度我们取一米杆直立在阳光下,其长为1.5米,在
同一时刻测得旗杆的影长为10.5米.旗杆的高度是 .
14.如图是置于水平地面上的一个球形储油罐,小敏想测量它的半径.
在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的
距离是10米(如示意图,AB=10米);同一时刻,他
又测得竖直立在地面上长为1米的竹竿的影子长为2
米,那么,球的半径是 米.
15.圆锥底面展开后是 ,侧面展开后是 .
三、用心想一想(每小题10分,共30分)
16.画出实物图(如图,上部分是长方体,下部是空心圆柱)的三视图.
17.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树。晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的。请你确定此时路灯光源 的位置.
18.要制作一个如图所示(图中阴影部分为底与盖,且SⅠ=SⅡ)的钢盒子,在钢片的四个角上分别截去两个相同的正方形与两个相同的小长方形,然后折合起来既可,求有盖盒子的高x.
第二十九章投影与视图复习测试题参考答案
1.D 2.C 3.C 4.D 5.A 6.B 7.B 8.A 9.B 10.B 11.圆台 12.中心投影
13.7米 14.2.5 15.圆、扇形 16.略 17.略 18.x=10cm
九年级下册第四章 投影与三视图 第 18 页 共 18 页
课题:4.1投影与盲区
教学目标:
1、经历实践、探索的过程,了解视点、视线、视角与盲区的概念;
2、体会视点、视线、视角、盲区在现实生活中的应用;
3、了解视点、视线、视角、盲区与中心投影的关系,感受其在生活中的实用价值。
教学重点:应用盲区的意义解释简单的现实现象。
教学难点:在简单的平面图和立体图中表示视线、视角和盲区。
教学过程:
一、创设情境,引入新课
(出示投影)你知道为什么飞机超低空飞行时,雷达很难发现它?
下图是人观察事物时的直观图,在这个图上涉及了哪些数学知识?(视线,视角,视点)
你能试着给它们下定义吗?
人在观察目标时,从眼睛到目标的射线叫做视线,眼睛所在的位置叫做视点,有公共视点的两条视线所成的角叫做视角。
做一做:课本:第70页
强调:视角与仰角和俯角的区别。
二、盲区的概念
如图4-2,小明在点O能看见站在幕布后面点C的小华吗?如果小明的位置不变,小华应怎样移动自己的位置,才能使小明看到自己?为什么?
学生讨论后得出:不能;移到幕布前∠AOB的范围内;因为小华在幕布后面的区域是小明视线不能到达的区域,要使小明看到自己,必须要移到小明视线能到达的区域。
教师追问:那么图中阴影部分的区域叫做什么?为什么?
小结:我们把视线不能到达的区域叫做盲区,如图4-2中的阴影部分的区域就是盲区。
如图4-3,∠AO1D,∠BO2C,分别表示人的双目水平位置上的最大视角(约120°),在这个图上什么地方是盲区,什么地方是人眼看得最清晰的区域?
盲区的意义还不局限于人观察景物,那么盲区的意义还有哪些应用呢?学生举例
三、应用新知
例 如图4-4,A,B表示教室的门框位置。小聪站在教室内的点P位置,小慧、小红、张杰三位同学分别站在教室外点C,D,E的位置。这三位同学中,小聪能看见谁?看不见谁?请用盲区的意义给出解释。
解:如图4-5,作射线PA,PB.图中阴影部分表示小聪观察教室外时的盲区.小慧、小红、张杰三位同学中,只有张杰在盲区内,所以小聪能看见的是小慧、小红,看不见的是张杰.
练习:课本第71页课内练习和作业题(由学生独立完成,后指名学生口答或板书)
四、 小结:
通过这节课的学习你学会了什么?你有什收获与困惑?
五、布置作业:见课课通第186页----第187页。
第19周第4课时上课时间1月5日(星期五)累计教案84个
课题:4.2投影(1)
教学目标:
1、经历实践探索,了解投影、投影面、及平行投影的概念;
2、体会并理解平行投影的特征,利用光的影子解决生活中的实际问题。
教学重点:理解平行投影的特征;
教学难点:在投影面上画出平面图形的平行投影。
教学过程:
一、创设情境
你看过皮影戏吗 皮影戏又名“灯影子”,是我国民间一种古老而奇特的戏曲艺术,在关中地区很为流行。皮影戏演出简便,表演领域广阔,演技细腻,活跃于广大农村,深受农民的欢迎。
放映电影《小兵张嘎》部分片段 ---小胖墩和他爸在日军炮台内为日本鬼子表演皮影戏
二、你知道吗
出示投影:
北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.
问题:那什么是投影呢?
物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影现象。光线叫做投射线,影子(也叫投影)所在的平面叫做投影面.
出示投影让学生感受在日常生活中的一些投影现象。
因为太阳离我们非常遥远,所以太阳光线可以看成平行光线,像这样的光线所形成的投影成为平行投影 ( parallel projection ).
三、问题探究(在课前布置,以数学学习小组为单位)
合作学习:在平行投影下,线段和平面图形的投影与图形本身、投影面、投射线之间的相对位置有什么关系? 请就此问题作一探讨。
1、以数学习小组为单位,观察在太阳光线下,木杆和三角形纸板在地面的投影。
2、 不断改变木杆和三角形纸板的位置,什么时候木杆的影子成为一点,三角形纸板的影子是一条线段?当木杆的影子与木杆长度相等时,你发现木杆在什么位置?三角形纸板在什么位置时,它的影子恰好与三角形纸板成为全等图形?还有其他情况吗?
3、根据前面的探索,你能解释下列示意图的实际意义吗?
四、概括新知,形成结构
1、物体在太阳光下形成的影子随着物体与投影面的位置关系的改变而改变, 当小棒、三角形等纸片与投影面平行时,它们的影子的大小和形状与原物全等,当小棒、三角形等纸片与太阳光线平行时,它们的影子形成一个点,一条线.。
某校墙边有甲、乙两根木杆。
2、应用新知:
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出此时乙木杆的影子吗?
学生尝试练习,一学生板书,后点评注意画图要整洁美观,规范,投射线画成虚线。
(2)地面上直立一根标杆AB如图,杆长为2cm。
①当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
②当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?并画出投影示意图;
(3)一个正方形纸板ABCD和投影面平行(如图),投射线和投影面垂直,点C在投影面的对应点为C’,请画出正方形纸板的投影示意图。
五、学习反思:
我们这节课学习了什么知识?
(1) 物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影;
(2) 太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影
(3) 物体在太阳光下形成的影子随着物体与投影面的位置关系的改变而改变,
1.当小棒、三角形等纸片与投影面平行时,它们的影子的大小和形状与原物全等.
2当小棒、三角形等纸片与太阳光线平行时,它们的影子形成一个点,一条线.
六、作业:
1、见课课通第188页,注意:第15题要解释题意
2、设计题:
北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.请通过查阅资料,上互联网等途径,收集我国古代有关日晷的历史背景,探索用日晷测定时刻的数学原理,并就此写一篇简要的报告.
第20周第1课时上课时间1月8日(星期一)累计教案85个
课题:4.2投影(2)
教学目标:
1、理解中心投影的概念,掌握和区别中心投影的投射线和平行投影的投射线具有不同的性质;
2、在观察、比较与归纳的探索过程zhogn,发现空间想象能力。
教学重点:中心投影的概念和区分中心投影和平行投影的区别;
教学难点:在投影面上画出平面图形的中心投影。
教学过程:
一、创设情景
投影出示:手影戏
二、归纳、应用新知
1、像皮影戏与手影戏这样由同一点的投射线所形成的投影叫做中心投影。
2、由于中心投影与平行投影的投射线具有不同的性质,因此,在这两种投影下,物体的影子也就有明显的差别。如图4-14,当线段AB与投影面平行时,AB的中心投影A‘B’把线段AB放大了,且AB∥A’B‘,△OAB~ OA‘B’.又如图4-15,当△ABC所在的平面与投影面平行时, △ABC的中心投影△A‘B’C‘也把△ABC放大了,从△ABC到△A‘B’C‘是我们熟悉的位似变换。
3、请观察平行投影和中心投影,它们有什么相同点与不同点?
平行投影与中心投影的区别与联系
区别 联系
光线 物体与投影面平行时的投影
平行投影 平行的投射线 全等 都是物体在光线的照射下,在某个平面内形成的影子。(即都是投影)
中心投影 从一点出发的投射线 放大(位似变换)
4、应用新知:(1)例2 图4-16的两幅图表示两根标杆在同一时刻的投影.请在图中画出形成投影的光线.它们是平行投影还是中心投影?并说明理由。
解:分别连结标杆的顶端与投影上的对应点(图4-17).很明显,图(1)的投射线互相平行,是平行投影.图(2)的投射线相交于一点,是中心投影。
(2)练习:课本第78页第1、2题
(3)例3 : 图4-18是两棵小树在路灯下的影子.请画出形成树影的光线,确定光源的位置.
解: 如图4-19,连结CB,FE,并延长相交于点O,则OC,OF就是形成树影的光线,点O就是光源所在的位置。
(4)练习:课本作业题第2、3、4 题。其中第4题要利用三角形相似知识有一定难度,要适当点拨。
三、小结:
1、由同一点出发的投射线所形成的投影叫做中心投影;
2、区别中心投影和平行投影关键在于投影线是否相交,若投射线相交于一点,则是中心投影,否则就是平行投影。
四、作业
见课课通第190—191页。
第20周第2课时上课时间1月9日(星期二)累计教案86个
课题:4.3简单物体的三视图(1)
教学目标:
1、了解正投影和简单立体图形的三视图的概念;
2、经历探索简单立体图形的三视图的画法,能识别物体的三视图;
3、培养动手实践能力,发展空间想象能力。
教学重点:简单立体图形的三视图的概念和画法
教学难点:简单立体图形的三视图的画法
教学过程:
一、创设情境,引入新课
“蒙古包”是蒙古族牧民住房的称呼。“包”,满语是“家”、“屋”的意思。蒙古族作为我国古老的游牧民族之一,他们的生活习性带有浓厚的游牧色彩。自古以来,这个生活在广阔的草原上,逐水草而居,以放牧牛羊为生的民族,大部分都从事着草原畜牧业。由于需要频繁地搬家,住房就必须是能够随意移动的活动房,古代又称这种活动房为“穹庐”、“毡帐”等,俗称“毡房”、“帐房”等。
如图所示的蒙古包的上部是圆锥,下部是圆柱体,你能画出它的三视图吗?
三视图与投影有什么关系?
指出:在平行投影中,如果投射线垂直于投影面,那么这种投影就称为正投影。
二、合作学习,探究新知
1、合作学习
这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
物体的正投影从一个方向反映了物体的形状和大小,为了全面地反映一个物体的形状和大小,我们常常再选择正面和侧面两个投影面,画出物体的正投影。
2、如图4-21,直三棱柱的正面方向的正投影是一个和矩形A1ACC1全等的矩形,这个矩形上、下两条边中点的连线,表示侧棱BB1的正投影;从左到右在侧投影面上的正投影也是一个矩形,它的一组对边等于直三棱柱的高,另一组对边等于直三棱柱底面三角形AC边上的高。
(1)你能试着画出它的三视图吗?
(2)如图4-21,这个直三棱柱的正面方向的正投影是什么形状?大小如何?你能描述一下吗?
(3)从左到右在侧投影面上的正投影是什么形状?大小如何?你能描述一下吗?
(4)分别转动水平和侧面的两个投影面,使三个正投影处于同一平面(如图4-22),就是我们所熟悉的三视图.
通过以上的学习,你有什么发现?
物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图,水平投影面上的正投影就是俯视图,侧投影面上的正投影就是左视图
三、应用新知
1、完成课本做一做
2、例1 一个圆锥如图4-23,底面直径为8㎝,高6㎝,画出它的三视图(比例为1:4)
分析:这个圆锥在正面的正投影是一个底边长为8㎝,高6㎝的等腰三角形;在水平面上的正投影是直径为8㎝的圆;在侧面上的正投影与正面上的正投影相同.
3、练习:课本第82页口答课内练习第1、2,作业题第2、3题和第4、5题(指名两学生板演)
四、小结
1、画一个立体图形的三视图时要考虑从某一个方向看物体获得的平面图形的形状和大小,不要受到该方向的物体结构的干扰。
2、在画三视图时,三个三视图不要随意乱放,应做到俯视图在主视图的下方,左视图在主视图的右边,三个视图之间保持:长对正,高平齐,宽相等。
五、作业:见课课通
第20周第3课时上课时间1月10日(星期三)累计教案87个
课题:简单物体的视图(2)
教学目标:
1、学会根据物体的三视图描述出几何体的基本形状或实物原型;
2、经历探索简单的组合几何体的三视图的画法,进一步发展空间想象能力。
教学重点与难点:根据物体的三视图描述出几何体的基本形状或实物原型
教学过程:
一、复习引入
说一说:直三棱柱、圆柱、圆锥、球的三视图
做一做:画出下列几何体的三视图
讲一讲:你知道正投影与三视图的关系
二、新课学习
例1 一个蒙古包如图所示,它上部的圆锥部分和下部的圆柱部分的高都是2m,底面直径为3m,请以1:200的比例画出它的三视图.
例2 一个六角螺帽的毛坯如图,底面正六边形的边长为250mm,高为 200mm,内孔直径为200mm.请画出六角螺帽毛坯的三视图.
3、课本的练习和作业题
三、小结:
1、一个视图不能确定物体的空间形状,根据三视图要描述几何体或实物原型时,必须将各视图对照起来看。
2、一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。例如:正方体的主视图是正方形,但主视图是正方形的几何体有直三棱柱、长方体、圆柱等。
3、对于较复杂的物体,有三视图形象出物体的原型,应搞清三个视图之间的前后、左右、上下的对应关系。
四、作业
见课课通地195---197页
第20周第4课时上课时间1月11日(星期四)累计教案88个
课题:第四章投影与三视图 复习
教学目标:
1、通过复习系统掌握本章知识,
2、体验数学来源于实践,又作用于实践。
3、提高解决问题分析问题的能力。
4、培养空间想象能力。
教学重点:投影和三视图
教学难点:画三视图
教学过程:
一、以提问形式小结本章知识
1、本章知识结构框架:
2、填空:
(1)人在观察目标时,从眼睛到目标的 叫做视线。 所在的位置叫做视点,有公共 的两条 所成的角叫做视角。
视线不能到达的区域叫做 。
(2)物体在光线的照射下,在某个 内形成的影子叫做 ,这时光线叫做 ,投影所在的 叫做投影面。
由 的投射线所形成的投影叫做平行投影。
由 的投射线所形成的投影叫做中心投影。
(3)在平行投影中,如果投射线 垂直于投影面,那么这种投影就称为正投影。
(4)物体的三视图是物体在三个不同方向的 。
上的正投影就是主视图,水平面上的正投影就是 , 上的正投影就是左视图。
二、例题讲解
例1、(1)在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A、小明的影子比小强的影子长 B、小明的影子比小强的影子短
C、小明和小强的影子一样长 D、无法判断谁的影子长
分析:阳光是平行光线,出现平行投影。路灯是点光源,是中心投影,形成的影子是不一样的
例2、如图所示图形是一个多面体的三视图,请根据视图说出该多面体的具体名称。
分析:从俯视图上看,该立体图形是个对称图形,从主视图、左视图上看,正面和左面都是等腰三角形,因此我们可以想象,该立体图形是正四棱锥。
例3、A、B 表示教室门口,张丽在教室内,王明、钱勇、李杰三同学在教室外,位置如图所示,张丽能看得见三位同学吗?请说明理由。
分析:画出最大视野也就是最大视角,就能确定盲区。
例4、如图,小王、小李及一根电线杆在灯光下的影子。
(1)确定光源的位置;
(2)在图中画出表示电线杆高度的线段。
分析:由条件易知,本题属于中心投影问题,根据中心投影的特点,物体与影子对应点的连线必须经过光源,因此我们可以利用两线的交点来求光源的位置。
例5、如图,是由一些大小相同的小正方体组成的简单的几何体的主视图和俯视图。
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值。
分析:左视图为侧视图,由于几何体只知道主视图和俯视图,那么左视图就不是唯一的,而主视图表示几何体共有三层,所以侧视图有多种可能,俯视图只看见5个小正方体,这5个正方体可分布在1、2、3层。
三、课外作业:见课本第86页的目标与评定。
第20周第5、6课时上课时间1月12日(星期五)累计教案89、90个
课题:第四章投影与三视图 测试卷
姓名: 分数:
一、精心选一选(每小题5分,共50分)
1.圆形的物体在太阳光的投影下是 ( )
(A)圆形. (B)椭圆形. (C)线段. (D)以上都不可能.
2.如图所示的圆台的上下底面与投影线平行,圆台的正投影是 ( )
(A)矩形. (B)两条线段.
(C)等腰梯形. (D)圆环.
3.如图摆放的几何体的左视图是 ( )
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
(A)小明的影子比小强的影子长. (B)小明的影子比小强的影子短.
(C)小明的影子和小强的影子一样长. (D)无法判断谁的影子长.
5.“圆柱与球的组合体”如图所示,则它的三视图是 ( )
6.下列左边的主视图和俯视图对应右边的哪个物体 ( )
7.小明在操场上练习双杠时,在练习的过程中他发现在地上双杠的两横杠的影子 ( )
(A)相交. (B)平行. (C)垂直. (D)无法确定.
8.在一个晴朗的好天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是 ( )
(A)上午. (B)中午. (C)下午. (D)无法确定.
9.如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是 ( )
(A)①②③④. (B)④①③②. (C)④②③①. (D)④③②①.
10.如图是“马头牌”冰激凌模型图,它的三视图是 ( )
二、耐心填一填(每小题4分,共20分)
11.右图是基本几何体的三视图,该基本几何体为 .
12.皮影戏中的皮影是由投影得到的 .
13.为测量旗杆的高度我们取一米杆直立在阳光下,其长为1.5米,在
同一时刻测得旗杆的影长为10.5米.旗杆的高度是 .
14.如图是置于水平地面上的一个球形储油罐,小敏想测量它的半径.
在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的
距离是10米(如示意图,AB=10米);同一时刻,他
又测得竖直立在地面上长为1米的竹竿的影子长为2
米,那么,球的半径是 米.
15.圆锥底面展开后是 ,侧面展开后是 .
三、用心想一想(每小题10分,共30分)
16.画出实物图(如图,上部分是长方体,下部是空心圆柱)的三视图.
17.与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树。晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的。请你确定此时路灯光源 的位置.
18.要制作一个如图所示(图中阴影部分为底与盖,且SⅠ=SⅡ)的钢盒子,在钢片的四个角上分别截去两个相同的正方形与两个相同的小长方形,然后折合起来既可,求有盖盒子的高x.
第二十九章投影与视图复习测试题参考答案
1.D 2.C 3.C 4.D 5.A 6.B 7.B 8.A 9.B 10.B 11.圆台 12.中心投影
13.7米 14.2.5 15.圆、扇形 16.略 17.略 18.x=10cm
九年级下册第四章 投影与三视图 第 18 页 共 18 页
