圆的综合复习[下学期]
图片预览

文档简介
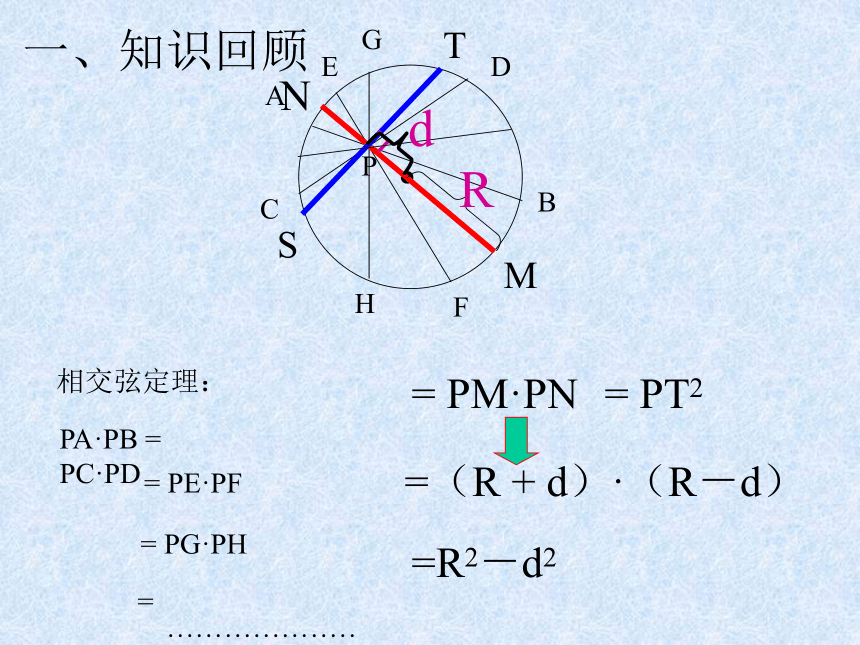
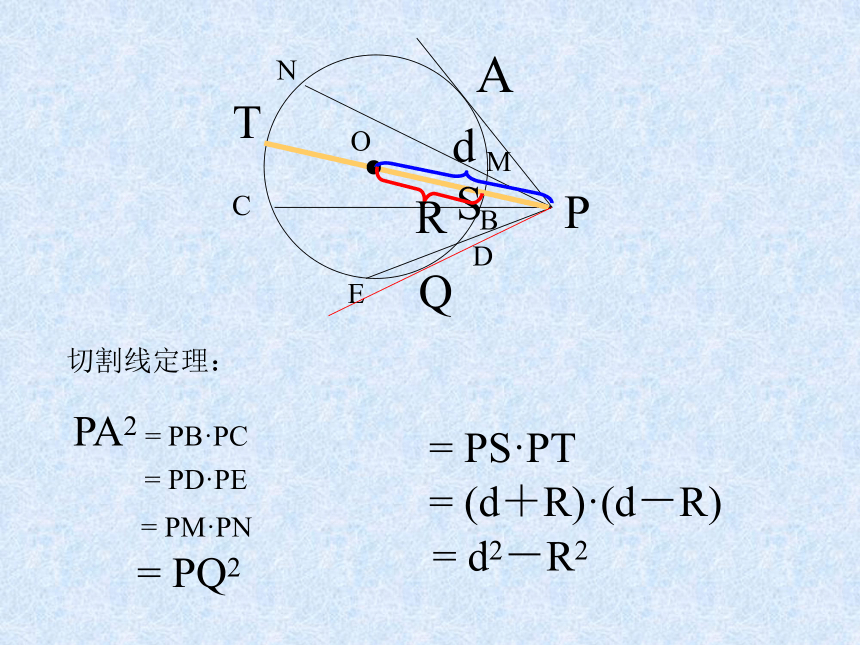
课件11张PPT。与圆有关的比例线段复习课ADBCPFE相交弦定理:PA·PB = PC·PDGH= PE·PF= PG·PH= ····················●MNST= PM·PN= PT2=(R + d)·(R-d)=R2-d2┓dR一、知识回顾ABCPO切割线定理:PA2 = PB·PCDEMN = PD·PE = PM·PNST● = PS·PTQ= PQ2 dR = (d+R)·(d-R) = d2-R21、已知:如图,AP=3cm,PB=5cm,CP=2.5cm,则
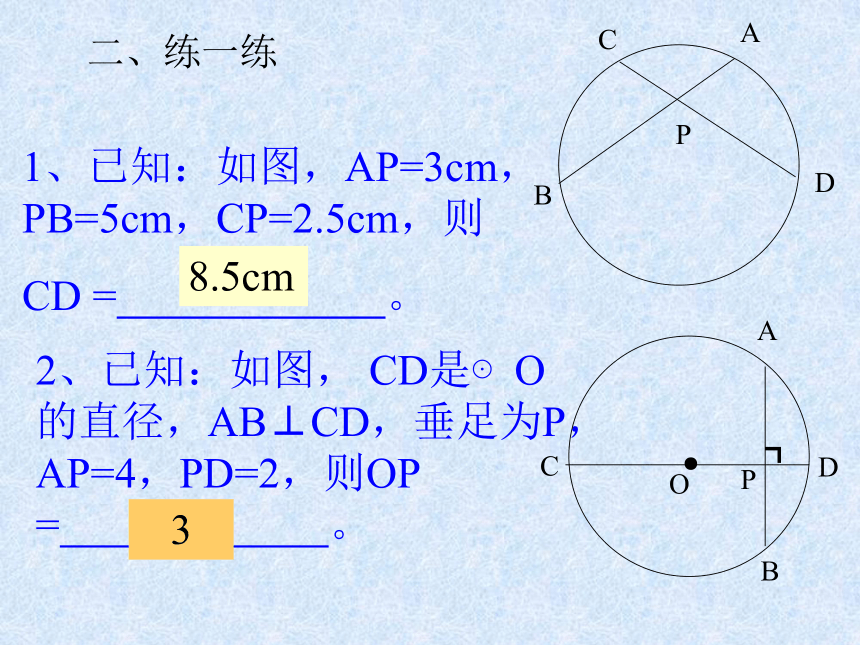
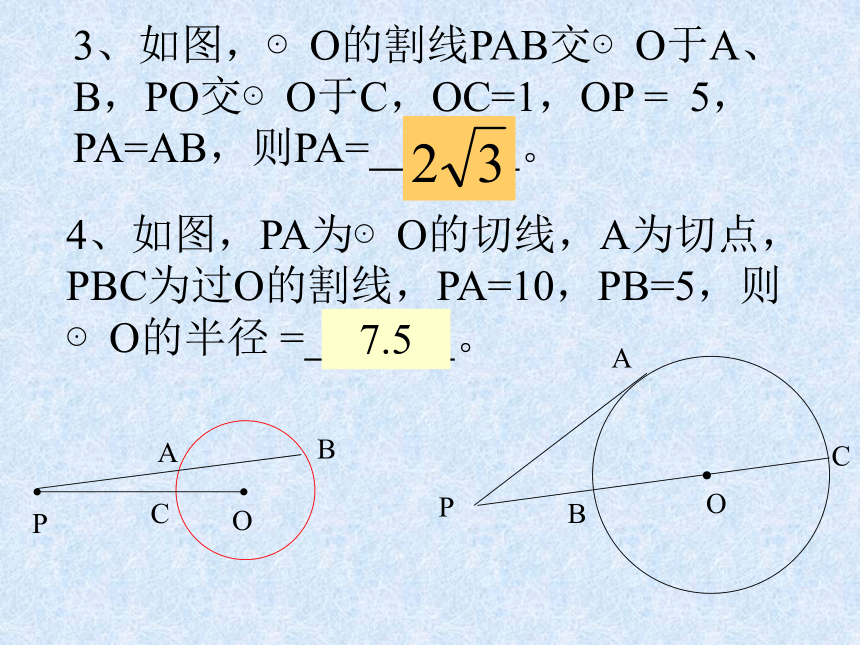
CD = 。PBCAD2、已知:如图, CD是⊙O的直径,AB⊥CD,垂足为P,AP=4,PD=2,则OP = 。PBCDA┓●O8.5cm3二、练一练3、如图,⊙O的割线PAB交⊙O于A、B,PO交⊙O于C,OC=1,OP = 5,PA=AB,则PA= 。4、如图,PA为⊙O的切线,A为切点,PBC为过O的割线,PA=10,PB=5,则⊙O的半径 = 。BAPOCPABOC●7.55、若圆内两弦相交,一弦长为16,且被交点平分,另一弦被交点分成两段的比是1∶4,则另一弦的长是 。206、P是圆外一点,PD为切线,D为切点,割线PE经过圆心O,若PF=12
,PD= ,则∠EFD=___度
30PDFEO三、典型例题分析●ODABC1、如图是两个同心圆O,大圆的弦AD,交小圆于B、C,且AB = BC = 4求圆环的面积。解:过O作OE⊥AD,垂足为E,E┓利用垂径定理易证:AB = CD过C作小圆的切线FG,交大圆于M、N,连结OC、ONNM∵AC · CD = CM · CN = CN2MN为小圆的切线 AC · CD = 8×4 = 32∴ CN2 = 32圆环的面积S = πON2-πOC2
=π( ON2-OC2 )
= πCN2
= 32π2、如图,以Rt△ABC的斜边AB为直径作⊙O,G为⊙O上一点,过点G作AB的垂线,分别交AB、AC和BC的延长线于D、E、F,求证:DG2 = DE · DFACDBFEGO●分析:∵ DG 2 = AD · BD∴只需证: DE · DF = AD · BD将上式化为比例式:∴ 只需证: △ADE∽△FDB┓┏问题得证。 3.已知:如图,在△ABC中,∠C=90°,BE是角平 分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆。 (1)求证AC是⊙O的切线; (2)若AD=6,AE=6 ,求DE的长。CAEDOB1、通过这节课的学习活动你有哪些收获?2、你还有什么问题吗?
CD = 。PBCAD2、已知:如图, CD是⊙O的直径,AB⊥CD,垂足为P,AP=4,PD=2,则OP = 。PBCDA┓●O8.5cm3二、练一练3、如图,⊙O的割线PAB交⊙O于A、B,PO交⊙O于C,OC=1,OP = 5,PA=AB,则PA= 。4、如图,PA为⊙O的切线,A为切点,PBC为过O的割线,PA=10,PB=5,则⊙O的半径 = 。BAPOCPABOC●7.55、若圆内两弦相交,一弦长为16,且被交点平分,另一弦被交点分成两段的比是1∶4,则另一弦的长是 。206、P是圆外一点,PD为切线,D为切点,割线PE经过圆心O,若PF=12
,PD= ,则∠EFD=___度
30PDFEO三、典型例题分析●ODABC1、如图是两个同心圆O,大圆的弦AD,交小圆于B、C,且AB = BC = 4求圆环的面积。解:过O作OE⊥AD,垂足为E,E┓利用垂径定理易证:AB = CD过C作小圆的切线FG,交大圆于M、N,连结OC、ONNM∵AC · CD = CM · CN = CN2MN为小圆的切线 AC · CD = 8×4 = 32∴ CN2 = 32圆环的面积S = πON2-πOC2
=π( ON2-OC2 )
= πCN2
= 32π2、如图,以Rt△ABC的斜边AB为直径作⊙O,G为⊙O上一点,过点G作AB的垂线,分别交AB、AC和BC的延长线于D、E、F,求证:DG2 = DE · DFACDBFEGO●分析:∵ DG 2 = AD · BD∴只需证: DE · DF = AD · BD将上式化为比例式:∴ 只需证: △ADE∽△FDB┓┏问题得证。 3.已知:如图,在△ABC中,∠C=90°,BE是角平 分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆。 (1)求证AC是⊙O的切线; (2)若AD=6,AE=6 ,求DE的长。CAEDOB1、通过这节课的学习活动你有哪些收获?2、你还有什么问题吗?
