二次函数复习[下学期]
图片预览






文档简介
课件25张PPT。 二次函数复习
·二次函数 的概念
·二次函数的图象特点
·二次函数的性质
·题型分析例1:已知二次函数y=x2-2x-8
(1)二次项,一次项系数,常数
(2)求二次函数的顶点坐标,对称轴,最值
(3)当x在什么范围内,y随x的增大而减小
(4)当x为何值时,y>0,x为何值时,y<0
(5)把二次函数y=x2-2x-8向左平移三个单位,再向下平移四个单位得到函数解析式为什么?
例1:已知二次函数y=x2-2x-8
(6)若函数与x轴两个交点为A,B,与y轴的交点为C,求△ABC的面积,若函数的顶点为P,求△ABP的面积。
(7)二次函数y=x2-2x-8与二次函数 关于y轴对称。
(8)画y=x2 y=x2-8 y=x2-2x的草图
(9)化二次函数y=x2-2x-8为顶点式和两根式。
例2.二次函数y=x2+bx+2
(1)若顶点在x轴上,则b=
(2)若顶点在y轴上,则b=
(3)若二次函数的最小值为1 则b=
(4)若二次函数在x=1时,有最小值,则 b=
(5)若二次函数经过(1,0),则b=
例3(1).y=6(x-1)(x+7)的对称轴是 最小值是 .
(2)若(-3,5)和(7,5)是某个二次函数上两点,则此 二次函数的对称轴是 .1.说出下列抛物线的开口方向、顶点坐标和对称轴:做一做:2。自变量x在什么范围内时,y随x的增大而增大,何时y随x的增大而减小?并求出函数的最大值或最小值?
3.化以上二次函数为顶点式。填空:
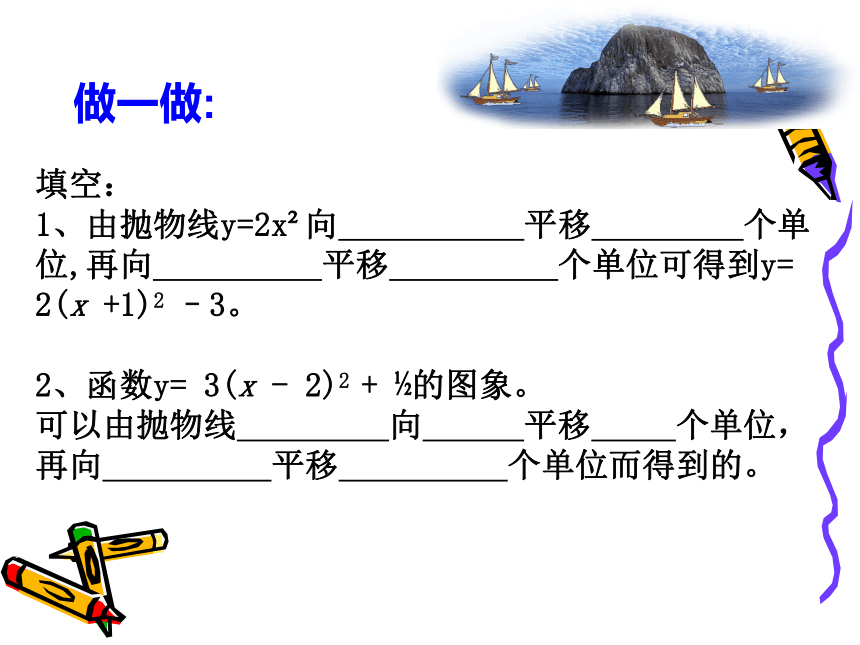
1、由抛物线y=2x2向 平移 个单位,再向 平移 个单位可得到y= 2(x +1)2 –3。
2、函数y= 3(x - 2)2 + ?的图象。
可以由抛物线 向 平移 个单位,
再向 平移 个单位而得到的。
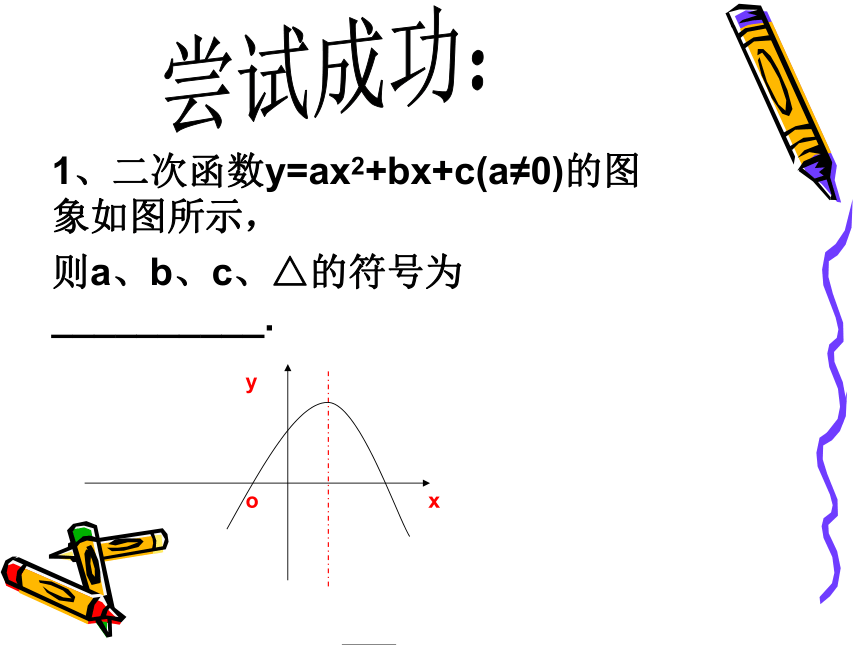
做一做:1、二次函数y=ax2+bx+c(a≠0)的图象如图所示,
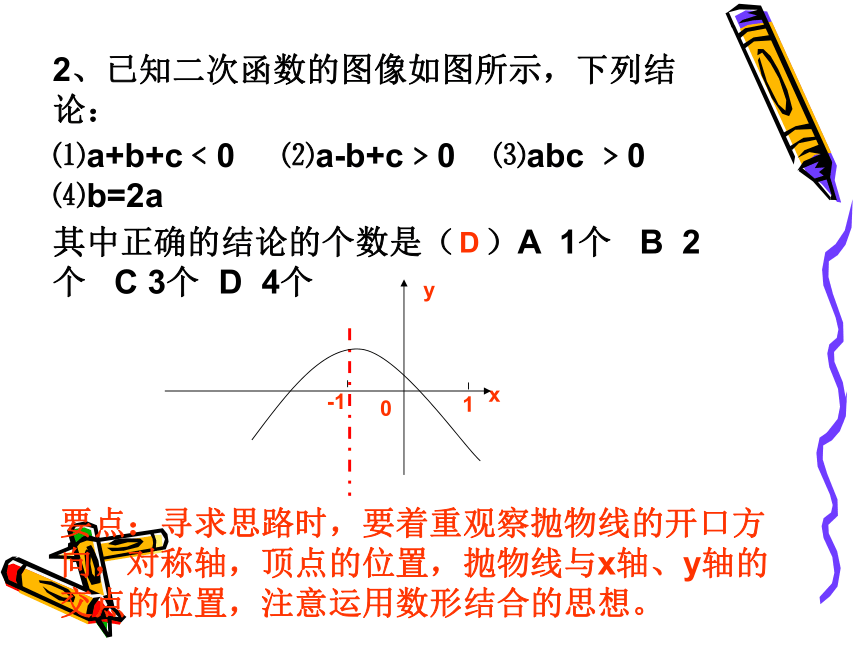
则a、b、c、△的符号为__________. 尝试成功:2、已知二次函数的图像如图所示,下列结论:
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是( )A 1个 B 2个 C 3个 D 4个Dx-110y要点:寻求思路时,要着重观察抛物线的开口方向,对称轴,顶点的位置,抛物线与x轴、y轴的交点的位置,注意运用数形结合的思想。1、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个练一练:3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中下正确的是()
A、abc>0
B、b2-4ac>0
C、2a+b>0
D、4a-2b+c<0题型分析:
(一)抛物线与x轴、y轴的交点所构成的面积
例1:填空:
(1)抛物线y=-2x2+5x-3与y轴的交点坐标是____________,与x轴的交点坐标是____________.
(2) 时 ,y>0; 时,y<0
(3)二次函数y=x2+bx+8的图像顶点在x轴的负
半轴上,那么b等于多少?
(0,-3)已知抛物线y=-x2+x+6, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。一抛物线y=-2x2的形状相同,顶点为(1,-4),则它的函数解析式为 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
(二)根据函数性质判定函数图象之间的位置关系答案: B已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )(A)(B)(C)(D)(三)由函数图象上的点的坐标求函数解析式已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8)。
(1)求这个二次函数的解析式;
(2)写出它的对称轴和顶点坐标。
答案:(1)y=-x2-2x
(2)对称轴:x=-1
顶点坐标(-1,1)1.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。 (1)求此二次函数的解析式; (2)设此二次函数的图象与x轴交于A,B两点,O为坐标原点,求线段OA,OB的长度之和。2.已知二次函数的图象与x轴交于(-1,0)和(6,0),
并且经过点(2,12),求二次函数解析式练习一:一座拱桥的示意图如图,当水面宽12m时,桥洞顶部离水面4m。已知桥洞的拱形是抛物线,要求该抛物线的函数解析式,你认为首先要做的工作是什么?如果以水平方向为x轴,取以下三个不同的点为坐标原点:
(1)点A,(2)点B,(3)抛物线的顶点C 得的函数解析式相同吗?请试一试。哪种取法求得的函数解析式最简单?问题1: 如图是某公园一圆形喷水池,水流在各方向沿形
状相同的抛物线落下。建立如图所示的坐标系,如果喷头所在
处A(0,1.25),水流路线最高处B(1,2.25),则该抛物线
的表达式为 。如果不考虑其他因素,那么水
池的半径至少要____米,才能使喷出的水流不致落到池外。y= -(x-1)2 +2.252.5问题2:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?分析:利润=(每件商品所获利润)× (销售件数) 设每个涨价x元, 那么(3)销售量可以表示为(1)销售价可以表示为(50+x)元(x≥ 0,且为整数)
(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元问题3
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQ解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:AP=2x cm PB=(8-2x ) cm QB=x cm则 y=1/2 x(8-2x)=-x2 +4x=-(x2 -4x +4 -4)= -(x - 2)2 + 4所以,当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2(0则 y=60-x2 -(10-x)(6-x)=-2x2 + 16x(0物线的顶点处到MN的距离是 4,要 在 铁皮上截
下一矩形ABCD,是矩形的顶点B、C落在 MN 上,
点A、D 落在抛物线上,问这样截下去的矩形铁
皮的周长能否等于 8,若能,求出矩形的长和宽。
若不能,说明理由。问题50MNABCDp问题6:一运动员推铅球,铅球经过的路线为如图所示的抛物线。 (1)求铅球所经过的路线的函数解析式和自变量取值范围。 (2)铅球的落地点离运动员有多远?y(m)
·二次函数 的概念
·二次函数的图象特点
·二次函数的性质
·题型分析例1:已知二次函数y=x2-2x-8
(1)二次项,一次项系数,常数
(2)求二次函数的顶点坐标,对称轴,最值
(3)当x在什么范围内,y随x的增大而减小
(4)当x为何值时,y>0,x为何值时,y<0
(5)把二次函数y=x2-2x-8向左平移三个单位,再向下平移四个单位得到函数解析式为什么?
例1:已知二次函数y=x2-2x-8
(6)若函数与x轴两个交点为A,B,与y轴的交点为C,求△ABC的面积,若函数的顶点为P,求△ABP的面积。
(7)二次函数y=x2-2x-8与二次函数 关于y轴对称。
(8)画y=x2 y=x2-8 y=x2-2x的草图
(9)化二次函数y=x2-2x-8为顶点式和两根式。
例2.二次函数y=x2+bx+2
(1)若顶点在x轴上,则b=
(2)若顶点在y轴上,则b=
(3)若二次函数的最小值为1 则b=
(4)若二次函数在x=1时,有最小值,则 b=
(5)若二次函数经过(1,0),则b=
例3(1).y=6(x-1)(x+7)的对称轴是 最小值是 .
(2)若(-3,5)和(7,5)是某个二次函数上两点,则此 二次函数的对称轴是 .1.说出下列抛物线的开口方向、顶点坐标和对称轴:做一做:2。自变量x在什么范围内时,y随x的增大而增大,何时y随x的增大而减小?并求出函数的最大值或最小值?
3.化以上二次函数为顶点式。填空:
1、由抛物线y=2x2向 平移 个单位,再向 平移 个单位可得到y= 2(x +1)2 –3。
2、函数y= 3(x - 2)2 + ?的图象。
可以由抛物线 向 平移 个单位,
再向 平移 个单位而得到的。
做一做:1、二次函数y=ax2+bx+c(a≠0)的图象如图所示,
则a、b、c、△的符号为__________. 尝试成功:2、已知二次函数的图像如图所示,下列结论:
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是( )A 1个 B 2个 C 3个 D 4个Dx-110y要点:寻求思路时,要着重观察抛物线的开口方向,对称轴,顶点的位置,抛物线与x轴、y轴的交点的位置,注意运用数形结合的思想。1、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个练一练:3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中下正确的是()
A、abc>0
B、b2-4ac>0
C、2a+b>0
D、4a-2b+c<0题型分析:
(一)抛物线与x轴、y轴的交点所构成的面积
例1:填空:
(1)抛物线y=-2x2+5x-3与y轴的交点坐标是____________,与x轴的交点坐标是____________.
(2) 时 ,y>0; 时,y<0
(3)二次函数y=x2+bx+8的图像顶点在x轴的负
半轴上,那么b等于多少?
(0,-3)已知抛物线y=-x2+x+6, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。一抛物线y=-2x2的形状相同,顶点为(1,-4),则它的函数解析式为 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
(二)根据函数性质判定函数图象之间的位置关系答案: B已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )(A)(B)(C)(D)(三)由函数图象上的点的坐标求函数解析式已知一个二次函数的图象经过点(0,0),(1,﹣3),(2,﹣8)。
(1)求这个二次函数的解析式;
(2)写出它的对称轴和顶点坐标。
答案:(1)y=-x2-2x
(2)对称轴:x=-1
顶点坐标(-1,1)1.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。 (1)求此二次函数的解析式; (2)设此二次函数的图象与x轴交于A,B两点,O为坐标原点,求线段OA,OB的长度之和。2.已知二次函数的图象与x轴交于(-1,0)和(6,0),
并且经过点(2,12),求二次函数解析式练习一:一座拱桥的示意图如图,当水面宽12m时,桥洞顶部离水面4m。已知桥洞的拱形是抛物线,要求该抛物线的函数解析式,你认为首先要做的工作是什么?如果以水平方向为x轴,取以下三个不同的点为坐标原点:
(1)点A,(2)点B,(3)抛物线的顶点C 得的函数解析式相同吗?请试一试。哪种取法求得的函数解析式最简单?问题1: 如图是某公园一圆形喷水池,水流在各方向沿形
状相同的抛物线落下。建立如图所示的坐标系,如果喷头所在
处A(0,1.25),水流路线最高处B(1,2.25),则该抛物线
的表达式为 。如果不考虑其他因素,那么水
池的半径至少要____米,才能使喷出的水流不致落到池外。y= -(x-1)2 +2.252.5问题2:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?分析:利润=(每件商品所获利润)× (销售件数) 设每个涨价x元, 那么(3)销售量可以表示为(1)销售价可以表示为(50+x)元(x≥ 0,且为整数)
(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元问题3
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQ解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:AP=2x cm PB=(8-2x ) cm QB=x cm则 y=1/2 x(8-2x)=-x2 +4x=-(x2 -4x +4 -4)= -(x - 2)2 + 4所以,当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2(0
下一矩形ABCD,是矩形的顶点B、C落在 MN 上,
点A、D 落在抛物线上,问这样截下去的矩形铁
皮的周长能否等于 8,若能,求出矩形的长和宽。
若不能,说明理由。问题50MNABCDp问题6:一运动员推铅球,铅球经过的路线为如图所示的抛物线。 (1)求铅球所经过的路线的函数解析式和自变量取值范围。 (2)铅球的落地点离运动员有多远?y(m)
同课章节目录
