二次函数（1）[下学期]

课件14张PPT。二次函数复习知识要点1.形如 的函数叫二次函数2.二次函数 的图象是一条 ,它关于 轴对称,顶点坐标是 ,当a＞0时,开口 ,顶点是抛物线上的最 点, 当a＜0时, 开口 ,顶点是抛物线上的最 点.抛物线y原点向上低向下高3.抛物线 可看做是抛物线 ,
先向 平移 个单位,再向 平移 个单位得到右3上44.二次函数 的图象是一条 ,它的对称轴是 ,顶点坐标是 ,当a＞0时,开口 ,顶点是抛物线上的最 点, 当a＜0时, 开口 ,顶点是抛物线上的最 点.抛物线向上低向下高课前基础训练1.下列函数中,是二次函数的是( )
B.
C. D.3.将函数　　　　　　　　进行配方，正确的结果应（　　）ＣＣ2.二次函数 的图象与x轴的两个交点坐标是( )
A.(0,0),(0,3) B.(0,0),(3,0)
C.(0,0),(0,-3) D.(0,0),(-3,0)B4.抛物线 的对称轴是( )
A.直线x=2 B.直线x=-2 C.直线x=4 D.直线x=-4A5.函数 的图象是以(3,2)为顶点的抛物线,则这个函数的关系式是(　　　）
Ｃ6.若抛物线 的顶点在x轴上,则c的值是( )
A.9 B.3 C.-9 D.0A7.已知二次函数 那么函数y的值( )
A.最小是1,最大是5 B.最小是1,无最大值
C.最小是3,最大是9 D.最小是1,最大是9Ｄ8.某旅行社有100张床位,每晚每床收费10元,客床可全部出租,若每床每晚提高2元,则减少10张床位出租,若每床每晚再提高2元,则再减少10张床位出租.已每次提高2元的这种方法变化下去,为了投资少而利润大,每床每晚应提高( )
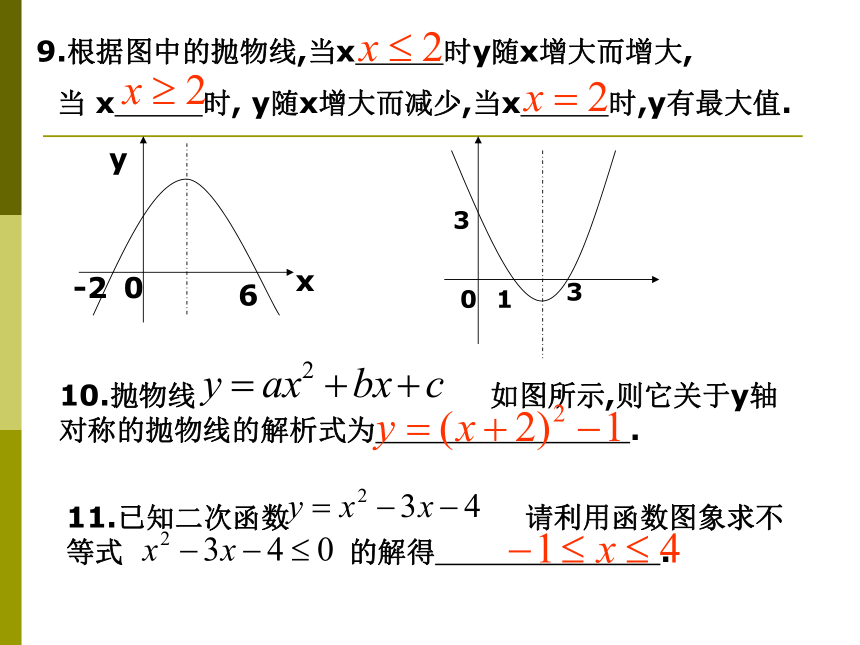
A.4元或6元 B.4元 C.6元 D.8元A9.根据图中的抛物线,当x 时y随x增大而增大,
当 x 时, y随x增大而减少,当x 时,y有最大值.10.抛物线 如图所示,则它关于y轴对称的抛物线的解析式为 .311.已知二次函数 请利用函数图象求不等式 的解得 .11.直线y=x+2与抛物线 的交点坐标是 ,12.已知二次函数 的顶点坐标是
(-1,-3.2)及部分图象如图,由图象可知一元二次方程
的两个根分别是x1=1.3和x2= .-3.3(-2,0)和(1,0)例题分析例1.已知一抛物线的顶点坐标为(-1,2),且过点(1,-2),
求该抛物线的解析式.例2.已知抛物线
(1)将函数化为 的形式.
(2)说出该函数图象可由抛物线 如何平移得到?
(3)说出该函数的对称轴,顶点坐标,最值情况.例3.已知二次函数
(1)当k为何值时，函数图象经过原点？
(2)当k在什么范围取值时，图象的顶点在第四象限？例题分析例4.已知抛物线 与x轴有交点,求实数k取值范围.例5.有砖和水泥,可砌长为48m的墙,要盖三间面积一样的平房,如图,问应怎样砌,才能使房屋的面积最大?课内练习1.将二次函数 的图象向左平移1个单位,再向下平移2个单位,求平移后抛物线解析式.2.二次函数 　　　的图象如图,试根据图象所给的信息,确定a,b,c的正负性，并说明理由．3.函数 　　　的图象如图所示.
(1)求a,b的值；（２）求图象与x轴的另一个交点p.1:已知 求证:
无论a为何值,抛物线与x轴都有2个交点.课内练习2.已知抛物线 与直线y=3x-1 交于A,B两点,求△AOB的面积.13.有一个二次函数的图象，三位学生分别说出了它的一些特点：
甲：对称轴是直线x=4;
乙：与x轴两个交点的横坐标都是整数；
丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形的面积为3 。
请你写出满足上述全部特点的一个二次函数解析式： 。